Data-Structures-And-Algorithms-Alfred-V-Aho

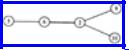
Data Structures and Algorithms: CHAPTER 7: Undirected Graphs

1.Start with M = Ø.

2.Find an augmenting path P relative to M and replace M by M Å P.

3.Repeat step (2) until no further augmenting paths exist, at which point M is a maximal matching.

It remains only to show how to find an augmenting path relative to a matching M. We shall do this for the simpler case where G is a bipartite graph with vertices partitioned into sets V1 and V2. We shall build an augmenting path graph for G for levels i = 0, 1, 2, . . . using a process similar to breadth-first search. Level 0 consists of all unmatched vertices from V1. At odd level i, we add new vertices that are adjacent to a vertex at level i-1, by a non-matching edge, and we also add that edge. At even level i, we add new vertices that are adjacent to a vertex at level i-1 because of an edge in the matching M, together with that edge.

We continue building the augmenting path graph level-by-level until an unmatched vertex is added at an odd level, or until no more vertices can be added. If there is an augmenting path relative to M, an unmatched vertex v will eventually be added at an odd level. The path from v to any vertex at level 0 is an augmenting path relative to M.

Example 7.10. Figure 7.19 illustrates the augmenting path graph for the graph in Fig. 7.17(a) relative to the matching in Fig. 7.18, in which we have chosen vertex 5 as the unmatched vertex at level 0. At level 1 we add the non-matching edge (5, 6). At level 2 we add the matching edge (6, 2). At level 3 we can add either of the non-matching edges (2, 9) or (2, 10). Since both vertices 9 and 10 are currently unmatched, we can terminate the construction of the augmenting path graph after the addition of either one of these vertices. Both paths 9, 2, 6, 5 and 10, 2, 6, 5 are augmenting paths relative to the matching in Fig. 7.18.

Fig. 7.19. Augmenting path graph.

Suppose G has n vertices and e edges. Constructing the augmenting path graphs for a given matching takes O(e) time if we use an adjacency list representation for edges. Thus, to find each new augmenting path takes O(e) time. To find a maximal matching, we construct at most n/2 augmenting paths, since each enlarges the current matching by at least one edge. Therefore, a maximal matching may be found in O(ne) time for a bipartite graph G.

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/mf1207.htm (18 of 22) [1.7.2001 19:15:36]

Data Structures and Algorithms: CHAPTER 7: Undirected Graphs

Exercises

Describe an algorithm to insert and delete edges in the adjacency list

7.1representation for an undirected graph. Remember that an edge (i, j) appears on the adjacency list for both vertex i and vertex j.

Modify the adjacency list representation for an undirected graph so that the first edge on the adjacency list for a vertex can be deleted in constant

7.2time. Write an algorithm to delete the first edge at a vertex using your new representation. Hint. How do you arrange that the two cells representing edge (i, j) can be found quickly from one another?

Consider the graph of Fig. 7.20.

a.Find a minimum-cost spanning tree by Prim's algorithm.

b.Find a minimum-cost spanning tree by Kruskal's algorithm.

c.Find a depth-first spanning tree starting at a and at

d.Find a breadth-first spanning tree starting at a and at d.

Fig. 7.20. A graph.

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/mf1207.htm (19 of 22) [1.7.2001 19:15:36]

Data Structures and Algorithms: CHAPTER 7: Undirected Graphs

Let T be a depth-first spanning tree and B be the back edges for a connected undirected graph G = (V, E).

a.Show that when each back edge from B is added to T a unique cycle results. Call such a cycle a basic cycle.

7.6

Implement both Prim's algorithm and Kruskal's algorithm. Compare the running times of your programs on a set of "random" graphs.

7.7Write a program to find all the connected components of a graph.

7.8

Write an O(n) program to determine whether a graph of n vertices has a cycle.

7.9

Write a program to enumerate all simple cycles of a graph. How many such cycles can there be? What is the time complexity of your program?

7.10

Show that all edges in a breadth-first search are either tree edges or cross edges.

7.11

Implement the algorithm for finding articulation points discussed in Section 7.4.

Let G = (V, E) be a complete graph, that is, a graph in which there is an edge between every pair of distinct vertices. Let G' = (V, E') be a

*7.12 directed graph in which E' is E with each edge given an arbitrary orientation. Show that G' has a directed path that includes every vertex exactly once.

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/mf1207.htm (20 of 22) [1.7.2001 19:15:36]

Data Structures and Algorithms: CHAPTER 7: Undirected Graphs

**7.13 Show that an n-vertex complete graph has nn-2 spanning trees.

7.14Find all maximal matchings for the graph of Fig. 7.16.

7.15Write a program to find a maximal matching for a bipartite graph.

Let M be a matching and let m be the number of edges in a maximal matching.

a. Prove there exists an augmenting path relative to M

Let M and N be matchings in a bipartite graph with ½M½ < ½N½. Prove

7.18that M Å N has at least ½N½ - ½M½ vertex disjoint augmenting paths relative to M.

Bibliographic Notes

Methods for constructing minimal spanning trees have been studied since at least Boruvka [1926]. The two algorithms given in this chapter are based on Kruskal [1956] and Prim [1957]. Johnson [1975] shows how k-ary partially ordered trees can be used to implement Prim's algorithm. Cheriton and Tarjan [1976] and Yao [1975] present O(e 1og log n) spanning tree algorithms. Tarjan [1981] provides a comprehensive survey and history of spanning tree algorithms.

Hopcroft and Tarjan [1973] and Tarjan [1972] popularized the use of depth-first search in graph algorithms. The biconnected components algorithm is from there.

Graph matching was studied by Hall [1948] and augmenting paths by Berge [1957] and by Edmonds [1965]. Hopcroft and Karp [1973] give an O(n2.5) algorithm for maximal matching in bipartite graphs, and Micali and Vazirani [1980] give an

algorithm for maximal matching in general graphs. Papadimitriou and

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/mf1207.htm (21 of 22) [1.7.2001 19:15:37]

Data Structures and Algorithms: CHAPTER 7: Undirected Graphs

Steiglitz [1982] contains a good discussion of general matching.

†Unless otherwise stated, we shall assume an edge is always a pair of distinct vertices.

†Note that MERGE and FIND are defined slightly differently from Section 5.5, since C is a parameter telling where A and B can be found.

‡We can initialize a partially ordered tree of e elements in O(e) time if we do it all at once. We discuss this technique in Section 8.4, and we should probably use it here, since if many fewer than e edges are examined before the minimum-cost spanning tree is found, we may save significant time.

Table of Contents Go to Chapter 8

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/mf1207.htm (22 of 22) [1.7.2001 19:15:37]

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/images/fig6_1.gif

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/images/fig6_1.gif [1.7.2001 19:15:54]

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/images/fig6_2.gif

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/images/fig6_2.gif [1.7.2001 19:16:11]

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/images/fig6_3.gif

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/images/fig6_3.gif [1.7.2001 19:16:26]

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/images/fig6_4.gif

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/images/fig6_4.gif [1.7.2001 19:16:34]

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/images/fig6_5.gif

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/images/fig6_5.gif [1.7.2001 19:16:51]