Глава 7. Вычисление неопределенных интегралов.

§1. Первообразная и неопределенный интеграл.

1. F(x) f(x) X F(x) = f(x) xX

Теорема. Пусть F(x) первообразная. G(x) - Первообразная той же функции  G(x) = F(x) + C , где С – постоянная.

§2. Таблица основных неопределенных интегралов.

Непосредственное интегрирование

§3. Метод замены переменной.

Вариант 1. Метод подведения под знак дифференциала.

u = (x) g(u) f(x)dx = g((x)) (x) dx = g(u) du

Вариант 2. Метод подстановки.

X x = (u) : U  X взаимно-однозначное отображение U на X  u = ^-1(x) : X  U

§4. Метод интегрирования по частям.

u(x) v(x) dx = u(x) v(x)  v(x) u(x) dx в краткой форме u dv = u v  v du

§5. Интегрирование рациональных дробей.

выделение целой части в случае m > n, дробная часть – правильная дробь

Разложение знаменателя на множители Q_n(x) =а₀ (x – ₁)…(x – _k)(x² + p₁x + q₁)…(x² + p_ix + q_i), p_l²– 4q_l <0

Разложение правильной дроби в сумму простейших дробей

Кратные корни  и т.д. «Логарифм + арктангенс»

§6. Интегрирование тригонометрических функций.

а) sin^mx cosⁿx dx Если хотя бы один из показателей степени нечетный – подведение под знак дифференциала. Если оба показателя четные – переход к двойному аргументу.

б) tg^2mx dx, ctg^2mx dx с помощью формул tg²x = cos^-2x – 1, ctg²x = sin^-2x – 1

в) R(sin x,cos x)dx, где R – рациональная функция,

с помощью подстановки

Если sin x и cos x в четных степенях, то с помощью подстановки tg x = t.

§7. Интегрирование некоторых иррациональных функций.

«Неберущиеся» интегралы. Таблицы интегралов.

Глава 8. Определенный интеграл и методы его вычисления.

§1. Определенный интеграл как предел интегральных сумм.

f(x) [a,b] a = x_o < x₁ <…< x_n = b разбиение отрезка

интегральная сумма, где x_k-1  c_k  x_k, x_k = x_k – x_k-1 max x_k  0

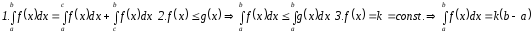
§2. Формула Ньютона-Лейбница.

Теорема (Барроу) fC[a,b], x(x) =  (x) дифференцируема на [a,b] и (x) = f(x)

Следствие 1. , поскольку(а) = 0

Следствие 2. Пусть F(x) – любая первообразная для f(x)  F(x) – F(a) = (x) – (a)

§3. Свойства определенного интеграла.

1. f(x)  0 на [a,b] 

2.

3. f  C[a,b], m  f(x)  M на [a,b] 

4. f  C[a,b]  с(a,b): среднее значение функции на [a,b]

5. f(x) четная  f(x) нечетная 

§4. Замена переменной и интегрирование по частям.

f  C[a,b], x=(t)  C¹[t₁,t₂], a =  (t₁), b =  (t₂)

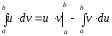
§5. Несобственные интегралы.

Интегралы с бесконечными пределами

f  C[a,+)  Сходящийся Расходящийся

Признаки сходимости (расходимости)

а) F(x) = f(x),   несобственный интеграл сходится и равен F(+) – F(a)

б) Пусть при а  х  + 0  f(x)  g(x) 

в) Пусть при а  х  + f(x) > 0, g(x) > 0 и , k  0, k  + 

Глава 9. Функции нескольких переменных

§1. Понятие функции нескольких переменных.

DRⁿ P(x₁,x₂,…,x_n)  D f(P) = f(x₁,x₂,…,x_n) f: Rⁿ  R E = uRu = f(P), PD

n = 2 z = f(x,y)  = (x,y,z)  R³ z=f(x,y)

§2. Предел и непрерывность.

A z = f(x,y) P(x,y)  P₀(x₀,y₀)  > 0 () > 0 : 0 < (P,P₀) = f(x,y) – A < 

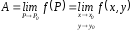
1) P₀  D 2)  3)

§3. Частные производные.

(x₀,y₀) z=f(x,y)

и т. д.

Смешанные частные производные ( не зависят от порядка дифференцирования )

§4. Дифференциал функции и его применение.

Полное приращение функции z=f(x,y) в точке Р(x₀,y₀) z = f(x₀+x, y₀+y) – f(x₀,y₀)

z = A₁x + A₂y +o() f(x₀ +x,y₀ +y)f(x₀, y₀) + df(x₀, y₀)

§5. Экстремум функции.

z=f(x,y) max(min) в точке Р(x₀,y₀) f(x₀, y₀)>f(x,y) ( f(x₀, y₀)<f(x,y) )

Необходимое условие экстремума

f_x(x₀,y₀) = f_y(x₀,y₀) = 0 или не существует, df(x,y)  0 Стационарная точка, критическая точка.

Достаточное условие экстремума

Р(x₀,y₀) A = f_xx(x₀,y₀), B = f_xy(x₀,y₀), C = f_yy(x₀,y₀), D = AC – B²

а) Если D > 0 , то Р(x₀,y₀) - точка экстремума, а именно: min при A>0 (C>0) , max при A<0 (C<0)

б) Если D < 0 , то экстремума нет. в) Если D = 0, требуется доп. исследование

Градиент f(x₀,y₀) = (f_x(x₀,y₀),f_y(x₀,y₀)) Производная по направлению f_l =f(x₀,y₀) cos

§6. Условный экстремум.

z=f(x,y) условный max(min) в точке Р(x₀,y₀) уравнение связи (х,у) = 0 ( условие ) f(x₀, y₀)>f(x,y) ( f(x₀, y₀)<f(x,y) )

Функция Лагранжа L(x,y,) = f(x,y) + (x,y),  - множитель Лагранжа.

Необходимое условие условногоэкстремума

L_x(x₀,y₀,₀) = 0, L_y(x₀,y₀,₀) = 0, L_(x₀,y₀,₀) = (x₀,y₀) = 0  Р₁(x₁,y₁,₁), Р₂(x₂,y₂,₂),…

Достаточное условие условногоэкстремума

< 0  P₁ – т. условного max,  < 0  P₁– т. условного min

§7. Наибольшее и наименьшее значения функции.

Во внутренней критической точке или в граничной точке

Граничные точки исследуют по частям границы.

Если функция линейна и ограничения линейны, то область многоугольна. В этом случае достаточно проверить углы.

§8. Метод наименьших квадратов.

х	х1	х2	…	xn
y	y1	y2	…	yn

y = ax + b Погрешности (отклонения в направлении оси Оу)

₁ = ax₁ + b – y₁, ₂ = ax₂ + b – y₂, …, _n = ax_n + b – y_n U = ₁²+₂²+…+_n² min

U = (ax₁ + b – y₁)² + (ax₂ + b – y₂)² +…+( ax_n + b – y_n)² = F(a,b) Необх. усл. экстремума F_a = 0, F_b = 0

i	xi	yi	xi2	xiyi
1	x1	y1	x12	x1y1
2	x2	y2	x22	x2y2
…	…	…	…	…
n	xn	yn	xn2	xnyn
	xi	yi	xi2	xiyi

Январь –4,8 Февраль – 4,4 Апрель – 4,6 Май – 4,6 Июль – 4,4 Сентябрь – ? Октябрь – ?