17

Основные понятия и аксиомы статики

1.1. Сила. Система сил. Равновесие абсолютно твердого тела

Как уже отмечалось во введении, в теоретической механике изучается движение материальных тел относительно друг друга. Для этого требуется, прежде всего, построить модели объектов и дать определение понятий, с которыми имеет дело механика. В теоретической механике рассматривается простейшая модель «обычного» евклидова трехмерного пространства. Постулируется, что в этом пространстве существует хотя бы одна система координат, в которой справедливы законы Ньютона (инерциальная система). Многочисленные опыты и измерения показывают, что с высокой степенью точности система отсчета с началом в центре Солнечной системы и осями, направленными к далеким «неподвижным» звездам, является инерциальной системой. В дальнейшем будет показано, что если существует хотя бы одна инерциальная система, то их имеется бесчисленное множество (инерциальные системы отсчета условно называются неподвижными).

В статике, не внося никаких погрешностей в вычисления, можно считать, что системы координат, жестко связанные с Землей, неподвижны. Условия относительного равновесия в других, неинерциальных системах отсчета, в частности, в системах, движущихся относительно Земли, будут выяснены в динамике.

Как для статики, так и для динамики одним из основных является понятие силы. Первичное представление о силе дают нам мускульные ощущения. В механике под силой понимается мера механического взаимодействия материальных тел, в результате которого взаимодействующие тела могут сообщать друг другу ускорения или деформироваться (изменять свою форму).

Из этого определения сразу вытекают два способа измерения сил: первый, динамический способ, основан на измерении ускорения тела в инерциальной системе отсчета, а второй, статический способ, основан на измерении деформации упругих тел.

В механике не изучают физическую природу сил. Укажем только, что силы могут возникать как при непосредственном контакте тел (например, сила тяги электровоза, передаваемая вагонам, сила трения между поверхностями соприкасающихся тел и т. п.), так и на расстоянии (например, силы притяжения небесных тел, силы взаимодействия электрически заряженных или намагниченных частиц и т. п.).

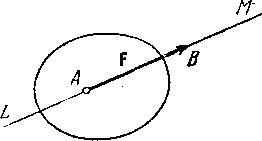
Сила является векторной величиной – она характеризуется численным значением или модулем, точкой приложения и направлением. Точка приложения силы и ее направление определяют линию действия силы.

На рис. 1.1 показана сила , приложенная в точке А, длина отрезка AB в соответствующем масштабе равна модулю силы, точка В называется концом силы; у конца силы ставится стрелка, указывающая направление действия силы. Прямая LM называется линией действия силы. Условимся

Рис.  1.1.

обозначать силу буквой жирного шрифта, например, , а ее модуль той же буквой обычного шрифта, т.е. F.

Для измерения модуля силы ее сравнивают с некоторой силой, выбранной в качестве единицы. В международной системе единиц измерения физических величин (СИ) за единицу силы принят один ньютон (1Н), а в технической системе единиц (система МКГСС) – один килограмм силы (1кГ или 1кгс – не следует смешивать с единицей массы в системе СИ — 1кг). Напомним, что эти единицы связаны соотношениями

1 кГ 9,81 Н; 1 Н  0,102 кГ.

Применяются и более крупные единицы измерения сил, в частности, 1 МН=10⁶ Н (меганьютон), 1 кН=10³ Н (килоньютон), 1 Т=1 тс = 10³ кГ (тонна) и т. п.

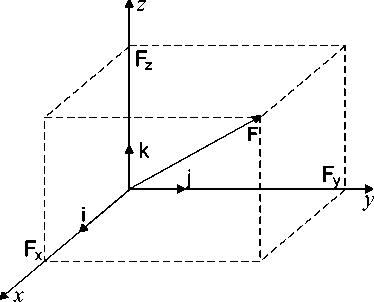
Силу часто задают непосредственным описанием, например: к концу балки приложена сила F, численно равная 5 кН и направленная вертикально вниз. Но можно задать силу и способом, которым обычно определяют векторы, а именно, через ее проекции на оси прямоугольной системы координат и точку приложения силы. Если, как обычно, единичные векторы (орты) осей обозначить через (рис. 1.2), то сила F определится точкой приложения и равенством

, (1.1)

где  – проекции силы на соответствующие координатные оси.

Рассматривая действие сил на материальные тела, мы будем отвлекаться не только от физической природы сил, но и от многих свойств самих тел. Так, реальные твердые тела обычно мало изменяют свою форму под действием приложенных к ним сил.

Рис. 1.2.

Поэтому для решения многих задач механики допустимо вовсе пренебречь малыми деформациями (т.е. малыми изменениями формы) и пользоваться моделью абсолютного твердого тела, понимая под ним тело, в котором расстояния между двумя любыми точками его остаются неизменными независимо от действия тех или иных сил. Для краткости мы будем часто пользоваться выражением «твердое тело» или даже просто «тело», имея в виду только что введенное понятие абсолютно твердого тела.

Совокупность нескольких сил называется системой сил. Если, не нарушая состояния тела, одну систему сил можно заменить другой системой и наоборот, то такие системы сил называются эквивалентными. Символически это обозначается следующим образом:

(1.2)

Введенное понятие эквивалентности систем сил не устанавливает условий, при выполнении которых две системы сил будут эквивалентны. Оно означает только, что эквивалентные системы сил вызывают одинаковое состояние тела (одинаковые ускорения или, если тело не абсолютно твердое, одинаковые деформации).

В том случае, когда система сил эквивалентна одной силе , т. е.

(1.3)

последняя называется равнодействующей данной системы сил. Это означает, что одна равнодействующая сила может заменить действие всех данных сил. В дальнейшем будет показано, что не всякая система сил имеет равнодействующую.

Как уже отмечалось, в инерциальной системе координат выполняется закон инерции. Это означает, в частности, что тело, находящееся в начальный момент в покое, останется пребывать в этом состоянии, если на него не действуют никакие силы. (Полная формулировка закона инерции будет дана в разделе динамики.) Если абсолютно твердое тело остается в состоянии покоя при действии на него системы сил , то последняя называется уравновешенной системой сил или системой сил, эквивалентной нулю:

(1.4)

Часто в этом случае говорят, что тело находится в равновесии.

В заключение этого параграфа обратим внимание на различие между понятием эквивалентности сил и понятием равенства векторов, изображающих эти силы. В математике два вектора считаются равными, если они параллельны, направлены в одну сторону и равны по модулю. Для эквивалентности двух сил этого недостаточно и из равенства еще не следует соотношение . Из сделанных определений

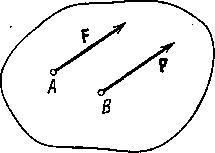
Рис. 1.3.

вытекает, что в общем случае две силы эквивалентны, если они геометрически (векторно) равны и приложены к одной точке тела. На рис. 1.3 показаны две геометрически равные, но не эквивалентные силы. В этом проявляется различие между свободными векторами, рассматриваемыми в математике, и силами.