Глава 1. Линейные системы и матрицы.

§1. n – мерное пространство Rⁿ

Вещественные числа (СПб) = действительные числа (М).

x₁, x₂, …, x_n – n-мерная точка M( x₁, x₂, …, x_n ).

Расстояние между M( x₁, x₂, …, x_n ) и N( y₁, y₂, …, y_n )

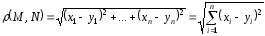
Вектор

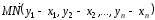
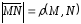
– радиус-вектор точки М.

Окрестность точки, ограниченное множество, замкнутое или открытое множество, предел последовательности n-мерных точек. Скалярное произведение.

Геометрически R¹ – прямая, R² – плоскость, R³ – пространство.

Множество наз.выпуклым, если

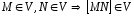
Свойство. V₁, V₂ – выпуклы 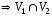выпукло.

§2. Системы линейных уравнений.

x₁, x₂, …, x_n

а₁x₁ +а₂x₂ +…+а_n x_n = b

k₁, k₂, …, k_n

x₁ = k₁, x₂ = k₂,…, x_n = k_n

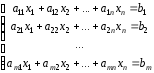
Матрица системы столбец правых частей

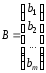размер m x n размерm x 1

Расширенная матрица системы 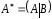размерm x (n+1)

Элементарные преобразования строк матрицы:

1. смена местами двух строк

2. умножение элементов строки на число

3. прибавление к элементам одной строки чисел, пропорциональных элементам другой строки

Преобразования обратимы. Система переходит в равносильную.

Если получается строка расширенной матрицы, состоящая из нулей – ее вычеркивают.

§3. Метод Гаусса. Метод Жордана.

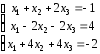
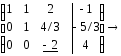
п р я м о й х о д

о б р а т н ы й х о д

b	x1	x2	x3	Решение системы методом Жордана ( Жордана-Гаусса )
-1	1	1	2	а11=1 – ключевой элемент: х1 исключается с помощью 1-го уравнения
4	1	-2	-2	из 2-й строки вычитается 1-я, умноженная на 1
-2	1	4	4	из 3-й строки вычитается 1-я, умноженная на 1
-1	1	1	2	ключевая строка делится на ключевой элемент
5	0	-3	-4	а22= -3 – ключевой элемент: х2 исключается с помощью 2-го уравнения
-1	0	3	2
2/3	1	0	2/3	из 1-й строки вычли измененную 2-ю (деленную на -3)
-5/3	0	1	4/3	ключевая строка делится на ключевой элемент (на -3)
4	0	0	-2	из 3-й строки вычли измененную 2-ю, умноженную на 3
2	1	0	0	из 1-й строки вычли измененную 3-ю, умноженную на 2/3
1	0	1	0	из 2-й строки вычли измененную 3-ю, умноженную на 4/3
-2	0	0	1	ключевая строка делится на ключевой элемент (на -2)

Бывают системы, не имеющие решений (несовместные), имеющие ровно 1 решение (см. пример) и имеющие бесконечное число решений.

несовместная имеет множество решений

§4. Действия над матрицами.

1. Сложение матриц

С=А+В, когда c_ij = a_ij + b_ij. Матрицы одного размера.

A+B=B+A, 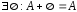,, (A+B)+C=A+(B+C)

2. Умножение матрицы на число

В=k^.А, когда b_ij = k^.a_ij Получается матрица того же размера.

(km)A=k(mA), 1^.A=A, 0^.A=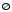. (k+m)A=kA+mA, k(A+B)=kA+kB

3. Умножение матрицы на матрицу.

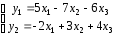
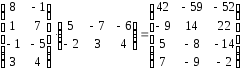
Правило: «строка 1-й матрицы на столбец 2-й матрицы по формуле скалярного произведения». Число столбцов 1-й матрицы должно быть равно числу строк 2-й.

А ^. В = С

mxnnxpmxpскалярное произведение

Свойства.1. (АВ)С=А(ВС) 2. 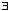E_m, E_n: E_m.A = A, A . E_n=A(единичные)

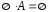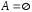3. 4. Если, то не обязательноили

5. 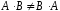даже для квадратных матриц 6. А(В+С)=АВ+АС, (А+В)С=АС+ВС

7. к(АВ)=(кА)В=А(кВ)

4. Транспонирование матриц– смена местами строк и столбцов.

Свойства.1. (А^Т)^Т=А 2. (А+В)^Т=А^Т+В^Т3. (кА)^Т=кА^Т4. (А^.В)^Т=В^Т.А^Т