Глава 6. Комплексные числа.
§1. Действия над комплексными числами.
Комплексное
число z
характеризуется парой вещественных
чисел (a,b)
с установленным порядком следования
z
= (a,b),
a
= Re
z
– вещественная часть, b
= Im
z
– мнимая часть.
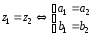
Сумма комплексных чисел z1+z2 = (a1+a2, b1+b2)Свойства. 1.z1+z2 = z2+z1 2. (z1+z2)+ z3 = z1+(z2+ z3)
Произведение z1.z2 = (a1a2 b1b2, a1b2 + a2b1)Свойства. 1.z1.z2 = z2.z1 2. (z1.z2). z3 = z1.(z2. z3) 3.(z1+z2). z3 = z1.z3+ z2.z3
(a,0)a. z z.(1,0) = z. (1,0)1. (0,b) – чисто мнимое число, (0,1) i – мнимая единица (0,b) = (b,0).(0,1) bi, i2 = 1 z = (a,b) = a + bi алгебраическая форма записи комплексного числа
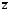= (a,
b)
= a
– bi
-
комплексно-сопряженное число
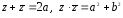
Деление
комплексных чисел z
= a
+ bi
=
§2. Геометрическая интерпретация комплексных чисел.
z = a + bi отождествляют с точкой x = a, y = b. Плоскость – комплексная, ось Ох – вещественная, ось Оу – мнимая.
Множество С множество точек комплексной плоскости множество свободных векторов.
При переходе к полярным координатам получают тригонометрическую форму комплексного числа
z = r ( cos + i sin )
r = z- модуль, = Arg z – аргумент. arg z [ -, ) или [ 0, 2 ) Arg z = arg z + 2k
Свойства. z1 + z2z1 + z2, z1 – z2z1 z2, z a, z b
§3. Формулы Эйлера и Муавра.
Формула Эйлера ei = cos + i sin z = r ei показательная форма записи комплексного числа.
При умножении комплексных чисел их модули умножаются, а аргументы складываются.
z1.z2 = r1 (cos 1 + i sin 1 ) .r2 (cos 2 + i sin 2 ) = r1r2 ( cos(1 + 2 ) + i sin(1 + 2 )), r1ei.r2ei = r1r2ei(+)
В частности, если z1 = z2 = z, то z2 = r2 (cos 2 + i sin 2), … , zn = rn (cos n + i sin n)
cos n + i sin n = (cos + i sin )n – формула Муавра
При делении …
§4. Извлечение корня из комплексного числа.
Если
z
= z1n
, то r
= r1n,
= n1
.
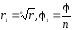Аргумент
определен не однозначно
,
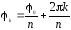где0
– одно из значений аргумента числа z.
различные
комплексные числа, которые при возведении
в n–ю
степень равны одному и тому же комплексному
числу z.
Модули этих чисел одинаковы – равны
r1
– т.е. они лежат на окружности. Аргументы
отличаются на число, кратное
.
Число различных корнейn-й
степени из равно n.
Точки на правильного n–угольника,
лежащего на окружности.
§5. Решение алгебраических уравнений.
f(z) = A0zn + A1zn-1 + … +An-1z + An , Ak R. (1) Пусть он имеет корень z = a + bi , b 0
z1
= a
– bi
также его корень.
.
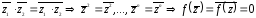Комплексные корни многочлена (1) распределяются по парам сопряженных корней.
Поскольку
,
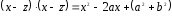то пара сопряженных корней дает
вещественный множитель 2-й степени сD<0
( при b0
)
многочлен n-й
степени можно разложить на множители
1-й и 2-й (с D<0
) степени.
Любой многочлен нечетной степени с вещественными коэффициентами имеет хотя бы 1 вещественный корень.
Если n = 2 и D<0, то уравнение имеет 2 комплексно-сопряженных корня.