Глава 4. Дифференцирование функций одной переменной.

§1. Определение производной.

f(x₀, x) = f(x₀ + x) – f(x₀) – приращение y = f(x) , соответствующее приращению x.

Производная 1-го порядка функции y = f(x) в точкеx₀ – это число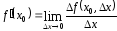

левая и правая производные.

f^(x₀)   f^_-(x₀), f^₊(x₀) и f^_-(x₀) = f^₊(x₀) f^(x₀)  f(x) непрерывна в точке x₀

Таблица производных основных элементарных функций.

1. (x^a)^/ = ax^a1, a  0. 2. (a^x)^/ = a^x lna, a > 0,a  1; (e^x)^/ = e^x. 3. (log_ax)^/ = log_aе /x, a > 0,a  1; (ln x)^/ = 1/x.

4. (sin x)^/ = cos x. 5. (cos x)^/ = sin x. 6. (tg x)^/ = 1/cos²x. 7. (ctg x)^/ = 1/sin²x.

8. (arcsin x)^/ = (arccos x)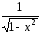^/ = . 9.(arctg x)^/ = (arcctg x)^/ = .

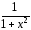§2. Правила дифференцирования.

1. (С)^/ = 0. 2. (f(x) + g(x))^/ = f^/(x) + g^/(x). 3. (Cf(x))^/ = Cf^/(x). 4. (f(x)g(x))^/ = f^/(x)g(x) + f(x)g^/(x). 5. .

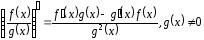6. Пусть f(x) имеет производную в т. x₀, а z = g(y) – в т. y₀ = f(x₀) 

z = g(f(x)) в т. x₀ имеет производную z^/(x₀) = g^/(y₀) f^/(x₀) – правило дифференцирования сложной функции.

7. Логарифмическая производная. .

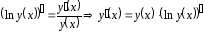§3. Дифференцирование функций, заданных неявно или параметрически.

Функция y = f(x), x(a,b) неявно задана уравнением F(x,y) = 0, если

x(a,b) F(x,f(x)) = 0 (1)

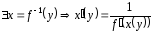производная обратной функции.

Пусть заданы x = (t), y = (t), t(a,b) (2).

Если t = ^1(x),то определена y(x) = (^1(x)), заданная параметрическими соотношениями (2) 

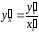
§4. Геометрический, механический, экономический смысл производной.

Уравнение касательной в точке М(х₀,у₀) y – y₀ = f^/(x₀)(x – x₀), нормали x – x₀ + f^/(x₀)( y – y₀) = 0

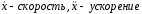
Скорость изменения экономических величин

х – затраты ресурса, f(x)  выпуск продукции  f^/(x)  предельный продукт

х – объем продукции, f(x) издержки производства  f^/(x) предельные издержки

§5. Дифференциал.

дифференцируемой в точке х₀ у(х₀,х) = Ах + о(х) (1)

Дифференциал Ax = dy(х₀,х) = dy(х₀,dх) y = f(x) дифференцируема в т.x₀ f^/( х₀) A = f^/( х₀)

y  dy при x<<1 y(х₀+х)  y(х₀) + f^/( х₀)х

§6. Теоремы Ферма, Ролля, Лагранжа, Коши.

Теорема 1 (Ферма). f(x) задана на <a,b>, дифференцируема в точке c и f(c) – экстремум  f^/(c) = 0

Доказательство (идея) f^/₊(c) = lim(  / + )  0, f^/_-(c) = lim(  / + )  0

Теорема 2 (Ролль). fC[a,b], fC¹(a,b), f(a) = f(b)  c(a,b): f^/(c) = 0

Доказательство (идея) 1.M = f(x)_наиб m = f(x)_наим 2. M = m  f^/(x)  0. 3. Mm  одно из этих двух чисел достигается внутри [a,b], в точке c(a,b). 4. По теореме 1 в этой точке f^/(c) = 0

Теорема 3 (Лагранж). fC[a,b], fC¹(a,b)  c(a,b): f(b) – f(a) = f^/(c) (b – a)

Доказательство (идея) 1.Находят вспомогательную функцию (x) = f(x) +kx: (a) = (b) 2. По теореме 2 c(a,b): ^/(c) = 0

Теорема 4 (Коши). f,gC[a,b], f,gC¹(a,b), g^/(x)  0  c(a,b):