Система сходящихся сил
2.1. Приведение системы сходящихся сил к равнодействующей
Силы называются сходящимися, если линии действия всех сил, составляющих систему, пересекаются в одной точке. Простейший случай трех сил был рассмотрен в главе I. Здесь рассматривается общий случай произвольного числа сил, образующих систему.
Существует немало практических задач, которые требуют исследования систем сходящихся сил; в частности, они возникают при расчетах шарнирно-стержневых систем (ферм). Кроме того, изучение системы сходящихся сил необходимо для дальнейших обобщений, относящихся к произвольной пространственной системе сил.
Прежде всего докажем теорему:
Система сходящихся сил эквивалентна одной силе (равнодействующей), которая равна сумме всех этих сил и проходит через точку пересечения их линий действия.
Пусть
задана система сходящихся сил
![]() ,
приложенных к абсолютно твердому телу
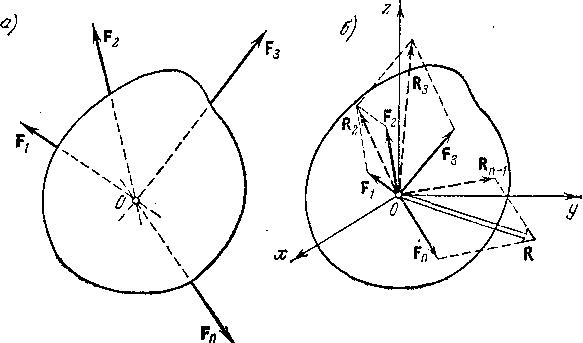
(рис. 2.1 а).
Согласно следствию из аксиомы 1
перенесем точки приложения сил по линиям
их действия в точку пересечения этих
линий (рис. 2.1 б).
Таким образом, мы получаем систему сил,
приложенных в одной точке. Она эквивалентна
исходной системе сходящихся сил.
Складывая теперь силы
,
приложенных к абсолютно твердому телу
(рис. 2.1 а).
Согласно следствию из аксиомы 1
перенесем точки приложения сил по линиям
их действия в точку пересечения этих
линий (рис. 2.1 б).
Таким образом, мы получаем систему сил,
приложенных в одной точке. Она эквивалентна
исходной системе сходящихся сил.
Складывая теперь силы
![]() и
и
![]() ,
на основании аксиомы 3 получим их
равнодействующую:
,
на основании аксиомы 3 получим их
равнодействующую:
![]() .
.
Индекс
в обозначении равнодействующей
соответствует номеру добавляемой силы
.
Затем, сложив силу
![]() с силой
с силой
![]() ,
найдем
,
найдем
![]() .
.
Сила
R3
является равнодействующей трех сил,
![]() ,
и равна их сумме. Дойдя, таким образом,
до последней силы
,
и равна их сумме. Дойдя, таким образом,
до последней силы
![]() ,
получим равнодействующую
,
получим равнодействующую
![]() всей системы
всей системы
![]() данных сил
данных сил
![]() . (2.1)
. (2.1)
Этим соотношением и доказывается справедливость сформулированной теоремы.
Построение равнодействующей может быть упрощено, если вместо параллелограммов построить силовой многоугольник. Пусть, например,
система
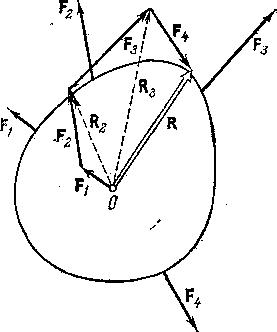
состоит из четырех сил (рис. 2.2). Если
от конца вектора
|
Рис. 2.1. |
помещая
его начало в конце вектора
.
Тогда мы получим вектор
![]() ,
идущий от точки
к концу вектора
.
Наконец, точно так же добавим вектор
,
идущий от точки
к концу вектора
.
Наконец, точно так же добавим вектор
![]() ;
при этом получим, что вектор, идущий от
начала первого вектора
к концу
вектора
,
является равнодействующей
.
;
при этом получим, что вектор, идущий от
начала первого вектора
к концу
вектора
,
является равнодействующей
.
Пространственный многоугольник, который получен указанным образом, называется силовым многоугольником.
На
рис. 2.2 показан разомкнутый
силовой
многоугольник (конец последней силы
не совпадает с началом первой силы);
равнодействующая
направлена по замыкающей силового
многоугольника. Конечно, при практическом
построении силового многоугольника
промежуточные равнодействующие
|
Рис. 2.2. |
Если для нахождения равнодействующей при помощи силового многоугольника используются правила геометрии или тригонометрии, то такой способ нахождения равнодействующей называется геометрическим способом.
В случае плоской системы сил можно воспользоваться плоским чертежом, откладывая силы в некотором масштабе; равнодействующая определяется непосредственным измерением по чертежу. Такой способ ее нахождения называется графическим.
Наиболее общим способом определения модуля и направления равнодействующей является аналитический способ, который также вытекает из основного соотношения (2.1). Поместим, например, начало прямоугольной системы координат в точку пересечения линий действия сил (см. рис. 2.1); тогда, пользуясь теоремой (она доказывается в курсе векторной алгебры), согласно которой проекция суммы векторов на некоторую ось равна сумме проекций на ту же ось слагаемых векторов, получим
 (2.2)
(2.2)
где
![]() – проекции
силы
– проекции
силы
![]() на указанные
оси, a
на указанные
оси, a
![]() –
проекции
равнодействующей на те же оси.
–
проекции
равнодействующей на те же оси.
Итак, проекции равнодействующей системы сходящихся сил на координатные оси равны алгебраическим суммам проекций этих сил на соответствующие оси.
С
помощью выражений (2.2) можно найти модуль
равнодействующей и ее направление в
прямоугольной системе координат
![]() .
.
Так как составляющие равнодействующей системы сил
![]() ,
, ![]() ,
, ![]() (2.3)
(2.3)
взаимно перпендикулярны (рис. 2.1), то модуль равнодействующей равен
 . (2.4)
. (2.4)
Направляющие косинусы равнодействующей соответственно равны
![]() ,
, ![]() ,
, ![]() . (2.5)
. (2.5)
В
частном случае, когда все силы расположены
в одной плоскости, удобно выбрать систему
координат
в плоскости
расположения сил. Тогда проекции всех
сил на ось
![]() равны нулю и
вместо формул (2.2), (2.4) и (2.5) будем иметь
равны нулю и
вместо формул (2.2), (2.4) и (2.5) будем иметь
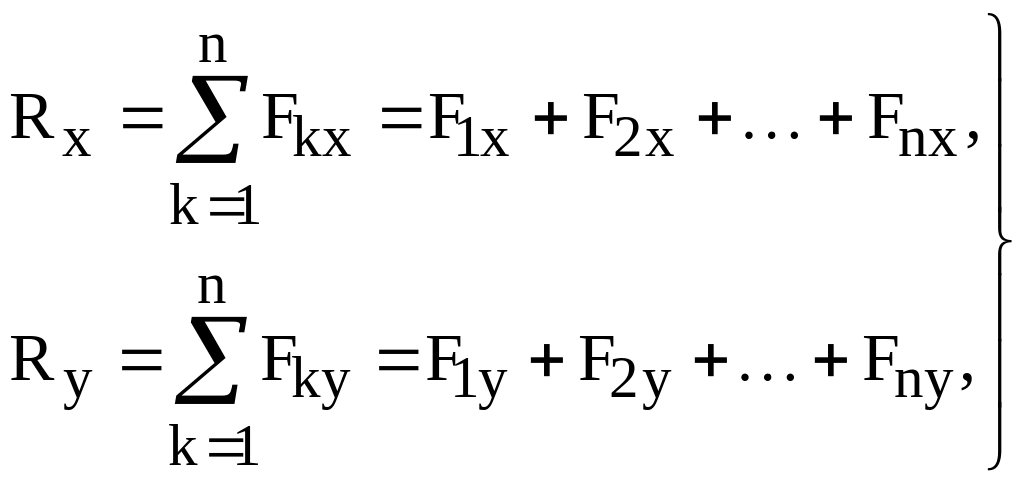 (2.6)
(2.6)
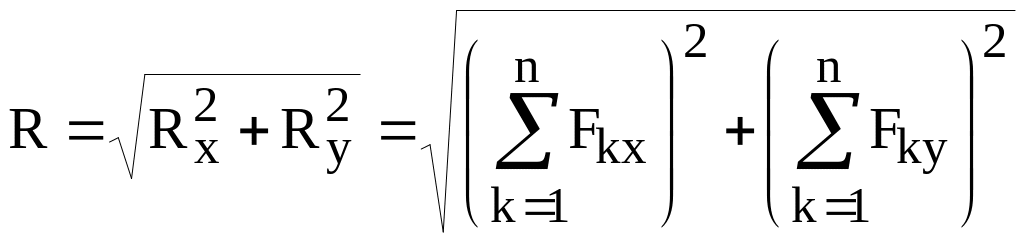 . (2.7)
. (2.7)
, . (2.8)