2.2. Условия равновесия системы сходящихся сил

При приведении системы сходящихся сил было показано, что такая система эквивалентна одной равнодействующей силе

.

Отсюда следует, что для равновесия тела, находящегося под действием системы сходящихся сил, необходимо и достаточно, чтобы равнодействующая их равнялась нулю:

. (2.9)

Следовательно, в силовом многоугольнике уравновешенной системы сходящихся сил конец последней силы должен совпадать с началом первой силы; в этом случае говорят, что силовой многоугольник замкнут (рис. 2.3). Это условие

Рис. 2.3.

удобно использовать при графическом решении задач для плоских систем сил.

Векторное равенство (2.9) эквивалентно трем скалярным равенствам:

. (2.10)

Принимая во внимание равенства (2.2), получаем аналитические условия равновесия:

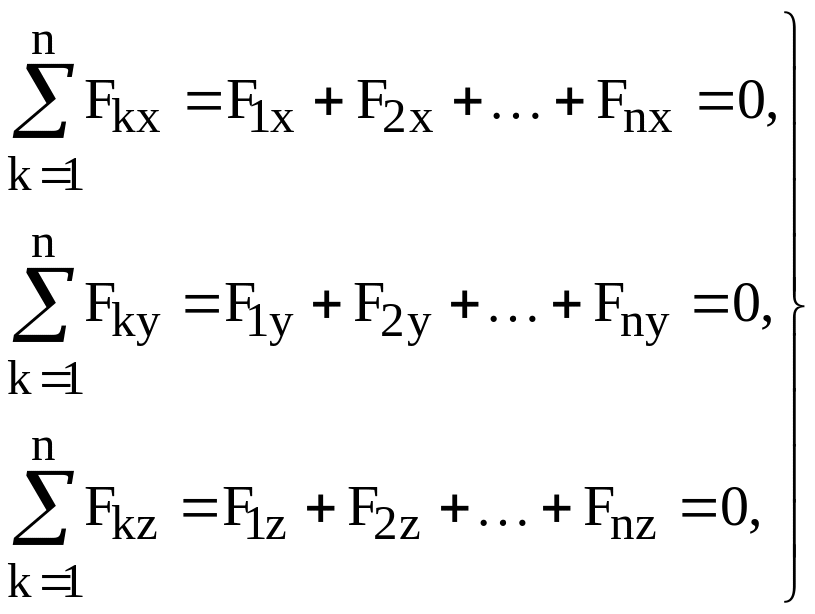(2.11)

т. е. для равновесия сходящейся системы сил необходимо и достаточно равенства нулю алгебраических сумм проекций всех сил данной системы на каждую из координатных осей.

Для частного случая плоскостей системы сходящихся сил, расположенных, например, в плоскости , третье условие (2.10) отпадает (т. е. обращается в тождество).

Очевидно, что условия равновесия (как в аналитической, так и в геометрической форме) позволяют проконтролировать, находится ли в равновесии заданная система сил.

Однако еще большее практическое значение имеет другая возможность использования этих условий. Часто заведомо известно, что вследствие наложенных связей тело находится в равновесии, причем мы знаем только часть действующих сил, а именно, активные силы; при этом опорные реакции известны лишь отчасти (например, известны их направления). Тогда с помощью условий равновесия можно найти остальные неизвестные, определяющие реакции связей. Условия равновесия, в которые входят неизвестные, будут уже служить уравнениями для определения этих неизвестных. Конечно, определение неизвестных возможно лишь в тех случаях, когда число неизвестных составляющих реакций не больше числа уравнений равновесия. Для определенности решения пространственной задачи на равновесие системы сходящихся сил она должна содержать не более трех неизвестных (соответственно трем уравнениям равновесия), а для плоской задачи – не более двух. Если неизвестных реакций больше, чем уравнений равновесия, в которые эти реакции входят, то задача не может быть решена только методами статики твердого тела (статически неопределимая задача). Хотя выбор направления координатных осей, на которые проектируются силы, не имеет принципиального значения, однако при решении задач для получения более простых уравнений равновесия рационально иногда направлять координатные оси перпендикулярно неизвестным силам; при этом некоторые уравнения равновесия будут содержать меньшее число неизвестных, чем их содержится в задаче.

2.3. Задачи

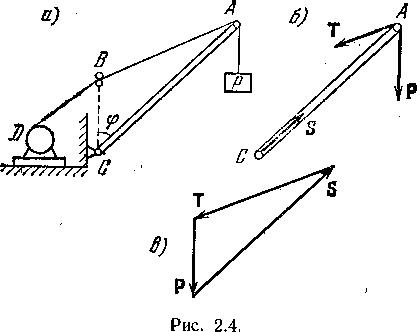
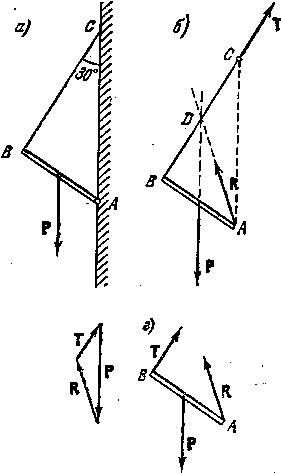
Задача 2.1. Кран состоит из стрелы АС, блоков В, троса ABD и мотора D. К концу А стрелы подвешен груз, вес которого равен Р. С помощью мотора D и троса стрелу можно установить под любым углом (рис. 2.4 а). Пренебрегая весом троса и стрелы, а также размерами

блоков В, определить натяжение троса и усилие в стреле, если известно расстояние и длина стрелы . Вычислить найденные величины при а=1,5 м, =4 м, =60, Р=6 тс.

Рассмотрим равновесие стрелы АС. В точке А к ней приложена активная сила (сила тяжести груза). В той же точке к ней приложена реакция троса ВА, направленная от А к В, а в точке С к стреле приложена реакция опоры С, направленная вдоль стрелы. Мысленно освободимся от связей и заменим их реакциями (рис. 2.4 б). Так как все три силы, , и , приложенные к стреле, уравновешены и пересекаются в одной точке А, то силовой треугольник должен быть замкнут.

Построение замкнутого треугольника сил следует начинать с известной силы . Из ее конца проводится направление силы (или ), а из начала силы проводится прямая, параллельная силе (или ), Точка пересечения этих прямых определяет силы и (рис. 2.4 в).

При отбрасывании связей было заранее предположено, что стрела (стержень) АВ сжата и поэтому реакция опоры С была направлена oт С к А. В данном примере это очевидно; в других, более сложных, случаях состояние стержня (растягивается он или сжимается) определяется решением задачи.

Треугольник сил PST подобен треугольнику ABC, образованному элементами крана (так как соответствующие стороны параллельны). Поэтому

.

Отсюда

, .

По условию задачи АС= , ВС=а. Пользуясь теоремой косинусов, из треугольника ABC найдем

.

Внося значения для АС, ВС и АВ в S и Т, получим

, .

При заданных значениях будем иметь

S=16 mс, Т=14 тс.

В заключение этого примера отметим, что при хорошем выполнении чертежа (строгое соблюдение масштабов и параллельности линий) приближенные значения усилия и натяжения можно определить без всяких вычислений простым измерением длин сторон силового треугольника. Недостаток графического метода состоит в том, что он не позволяет провести анализ полученного решения, так как численные значения искомых величин отвечают одному фиксированному положению механизма.

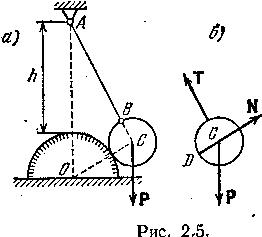
Задача 2.2. Шар веса Р и радиуса удерживается нитью АВ длины на неподвижной гладкой цилиндрической поверхности радиуса (рис. 2.5 а). Определить натяжение нити и давление шара на опорную поверхность, если точка А

в)

крепления нити лежит на одной вертикали с центром О цилиндрической поверхности.

Рассмотрим равновесие шара. Мысленно освободим шар от связей и заменим их реакциями (рис. 2.5 б). Реакция нити , равная ее натяжению, направлена вдоль нити от В к А; реакция N гладкой цилиндрической поверхности направлена по нормали к поверхности (она приложена к шару в точке D касания шара с опорной поверхностью и направлена по нормали к поверхности шара, т.е. по радиусу DC). Шар находится в равновесии под действием трех сил: Р, N и Т. Построив замкнутый силовой треугольник (из конца известной силы Р проводим прямую, параллельную DC, а из начала силы Р прямую, параллельную ВА; точка пересечения этих прямых определяет конец силы N и начало силы Т; рис. 2.5 в), мы можем определить модули сил N и Т с помощью масштаба простым измерением их длины. В данном примере легко использовать аналитические методы. Действительно, из подобия треугольника ОСА (рис.  2.5 а) и силового треугольника PNT следует

.

Отсюда найдем

, .

Давление шара N' на опорную поверхность (аксиома 4) равно по модулю реакции N, но направлено в противоположную сторону: N'= –N.

Задача 2.3. Однородная балка длины и веса Р удерживается в равновесии нитью ВС и шарниром А (рис. 2.6 а). Найти натяжение нити и реакцию шарнира А, если ВСА=30, ABC=90°. Рассмотрим равновесие системы, состоящей из балки и нити. Мысленно освободим систему от связей в точках А и С и приложим в этих точках 'реакции (рис. 2.6 б). К балке приложены сила тяжести Р, сила натяжения нити Т и реакция

Рис. 2.6.

шарнира R. Эта система сил должна быть эквивалентна нулю. По теореме о трех непараллельных силах реакция R должна проходить через точку D (середину стороны ВС). Построим силовой треугольник (рис. 2.6 в). Из подобия силового треугольника и треугольника ADC (рис. 2.6 б) следует, что

.

Подставляя сюда , , ,

Получим , .

Начало этих рассуждений может быть несколько видоизменено, если рассматривать равновесие балки, отделенной как от стены (в точке А), так и нити (в точке В); см. рис. 2.6 г. Однако последующие выкладки останутся прежними, в частности, тем же останется силовой треугольник на рис. 2.6 в.

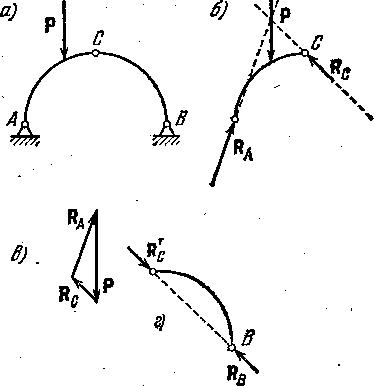
Задача 2.4. Определить реакции опорных шарниров невесомой трехшарнирной арки ABC, левая половина которой нагружена силой Р (рис. 2.7. а). Рассмотрим равновесие каждой полуарки отдельно. К правой полуарке приложены две силы: реакция в шарнире В и реакция R’С левой полуарки на правую. Значит, линии действия этих сил проходят

Р ис. 2.7.

через В и С. Левая полуарка (рис. 2.7 б) находится в равновесии, следовательно, силы Р, R_А, и R_С образуют уравновешенную систему и линия действия реакции R_А проходит через точку пересечения линий действия силы Р и реакции R_С (реакции правой полуарки на левую). Так как направления всех сил известны, то можно построить силовой треугольник (рис. 2.7 в) и определить величины искомых реакций. После этого можно построить систему сил для правой полуарки; это сделано на рис. 2.7 г, причем

R’_С=R_В= R_С.

Задача 2.5. Однородный цилиндр веса Р расположен между двумя гладкими наклонными плоскостями, образующими с горизонтом углы и (рис. 2.8 а). Определить силы давления цилиндра на обе опорные плоскости.

Так как плоскости гладкие, то их реакции R1 и R2 (рис. 2.8 б) направлены перпендикулярно плоскостям, т.е. направлены к оси цилиндра и вместе с силой Р образуют сходящуюся систему сил. Запишем уравнения равновесия этой

Рис. 2.8.

системы сил:

,

,

откуда находим , .

Искомые силы давления и будут равны (согласно аксиоме 4) по модулю и противоположны по направлению реакциям и .

Задача 2.6. Горизонтальная балка АВ удерживается в равновесии стержнями АС и AD. Найти усилия в стержнях и балке, если к концу А балки приложена сила Р, перпендикулярная балке и образующая с вертикалью угол .

Дано: ОАВ= , DAO=САО= . Весами балки и стержней пренебречь; крепления шарнирные (рис. 2.9 а).

Заменяя действие стержней и балки на узел А реакциями , получим систему четырех сил, приложенных в одной точке А (рис. 2.9 б).

Проекции этих сил на координатные оси (систему координат см. на рис. 2.9 б) равны:

Проекции	Силы
	Р
	0
				0
				0

Поэтому в соответствии с условиями (2.11) уравнения равновесия данной системы сил имеют вид

,

,

.

Откуда ,

,

.

Усилия в стержнях и балке соответственно равны найденным реакциям .

Если бы балка поддерживалась большим числом стержней, то задача стала бы статически неопределимой, поскольку число неизвестных превзошло бы число уравнений.

Задача 2.7. Невесомые стержни АВ и АС, соединенные в точке А шарниром, поддерживаются в равновесии нитью AD. Определить натяжение нити и усилия в стержнях, если ABC=ACB= =45°, АЕО= =30°, а к точке А приложена горизонтальная сила F=2 кГ, линия действия которой образует с плоскостью yz угол (рис. 2.10 а). Концы стержней В к С закреплены шарнирно. Прямая ВС горизонтальна.

Заменим действие стержней и нити на узел А реакциями и Т. Проекции сил и Т на оси координат будут (рис. 2.10 б):

Проекции	Силы
				Т
				0
				0
	0

Составим уравнения равновесия:

Рис. 2.9.

,

,

.

Отсюда ,

,

.

Натяжение нити и усилия в стержнях соответственно равны полученным значениям и .

Если , то  кГ,  кГ.

При  кГ,  кГ,  кГ.

(знак минус в выражении для означает, что стержень АС сжат, а не растянут, как предполагалось при построении реакций).

При усилие в стержне АС равно нулю.