1.2. Аксиомы статики и их следствия

В аксиомах статики формулируются те простейшие и общие законы, которым подчиняются силы, действующие на одно и то же тело, или силы, приложенные к взаимодействующим телам. Эти законы установлены многочисленными непосредственными наблюдениями, а также опытной проверкой следствий (часто далеких и вовсе не очевидных), логически вытекающих из этих аксиом.

Как следует из второго закона Ньютона, тело под действием одной силы приобретает ускорение и, следовательно, оно не может находиться в покое. Это означает, что одна сила не может составлять уравновешенную систему сил. Первая аксиома устанавливает условия, при выполнении которых, простейшая система сил будет уравновешена.

Аксиома 1. Две силы, приложенные к абсолютно твердому телу, будут уравновешены (эквивалентны нулю) тогда и только тогда, когда они равны по модулю, действуют по одной прямой и направлены в противоположные стороны.

Рис. 1.4.

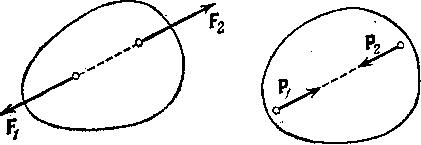
Это означает, что если абсолютно твердое тело находится в покое под действием двух сил, то эти силы равны по модулю, действуют по одной прямой и направлены в противоположные стороны. Обратно, если на абсолютно твердое тело действуют по одной прямой в противоположные стороны две равные по модулю силы и тело в начальный момент находилось в покое, то состояние покоя тела сохранится.

На рис. 1.4 показаны уравновешенные силы и , удовлетворяющие соотношениям: , . При решении некоторых задач статики приходится рассматривать силы, приложенные к

Рис. 1.5.

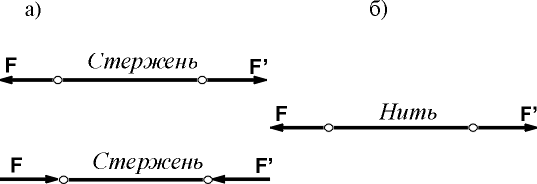
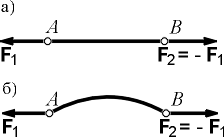
концам жестких стержней, весом которых можно пренебречь, причем известно, что стержни находятся в равновесии. Из сформулированной аксиомы непосредственно следует, что действующие на такой стержень силы направлены вдоль прямой, проходящей через концы стержня, противоположны по направлению и равны друг другу по модулю (рис. 1.5, а). Этот вывод сохраняется и в случае, когда ось стержня криволинейная (рис. 1.5, б).

Первая аксиома устанавливает необходимые и достаточные условия уравновешивания только двух сил, но, конечно, уравновешенная система сил может состоять и из большего числа сил. Две следующие аксиомы устанавливают простейшие действия с силами, при которых состояние тела не изменяется.

Аксиома 2. Не нарушая состояния абсолютно твердого тела, к нему можно прикладывать или отбрасывать силы тогда и только тогда, когда они составляют уравновешенную систему, в частности, если эта система состоит из двух сил, равных по модулю, действующих по одной прямой и направленных в противоположные стороны.

Из этой аксиомы вытекает следствие: не нарушая состояния тела, точку приложения силы можно переносить вдоль линии ее действия.

Действительно, пусть сила приложена к точке А (рис. 1.6, а). Приложим в точке В на линии действия силы уравновешенные силы две уравновешенные силы и , полагая, что (рис. 1.6, б). Тогда

Р ис. 1.6

согласно аксиоме будем иметь .Так как силы и образуют также уравновешенную систему сил (аксиома 1), то согласно аксиоме 2 их можно отбросить (рис. 1.6, в). Таким образом,

,

или

,

что доказывает следствие.

Это следствие показывает, что сила, приложенная к абсолютно твердому телу, представляет собой скользящий вектор.

Обе аксиомы и доказанное следствие нельзя применять к деформируемым телам, в частности, перенос точки приложения силы вдоль линии ее действия меняет напряженно-деформированное состояние тела.

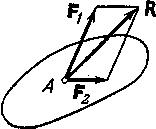
Аксиома 3. Не меняя состояния тела, две силы, приложенные к одной его точке, можно заменить одной равнодействующей силой, приложенной в той же точке и равной их геометрической сумме (аксиома параллелограмма сил).

Рис. 1.7.

Эта аксиома устанавливает два обстоятельства: первое – две силы и (рис. 1.7), приложенные к одной точке, имеют равнодействующую, т.е. эквивалентны одной силе

;

второе – аксиома полностью определяет модуль, точку приложения и направление равнодействующей силы

. (1.5)

Другими словами, равнодействующую можно построить как диагональ параллелограмма со сторонами, совпадающими с и .

Модуль равнодействующей определится равенством

,

где  – угол между данными векторами и .

Отметим, что третья аксиома применима к любым, не обязательно абсолютно твердым телам.

Вторая и третья аксиомы статики дают возможность переходить от одной системы сил к другой системе, ей эквивалентной.

В частности, они позволяют разложить любую силу на две, три и т.д. составляющие, т.е. перейти к другой системе сил, для которой сила является равнодействующей. Задавая, например, два направления, которые лежат с в одной плоскости, можно построить параллелограмм, у которого диагональ изображает силу . Тогда силы, направленные по сторонам параллелограмма, составят систему, для которой сила будет равнодействующей (рис. 1.7). Аналогичное построение можно провести и в

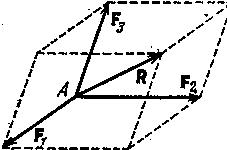
пространстве. Для этого достаточно из точки приложения силы R провести три прямые, не лежащие в одной плоскости, и построить на них параллелепипед с диагональю, изображающей силу , и с ребрами, направленными по этим прямым (рис. 1.8).

Рис. 1.8.

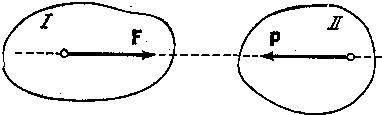
Аксиома 4. (3-й закон Ньютона). Силы взаимодействия двух тел равны по модулю и направлены по одной прямой в противоположные стороны.

Заметим, что силы взаимодействия двух тел не составляют систему уравновешенных сил, так как они приложены к разным телам.

Если тело I действует на тело с силой , а тело II действует на тело I с силой (рис. 1.9), то эти силы равны

Рис. 1.9.

по модулю и направлены по одной прямой в противоположные стороны, т. е. .

Если обозначить через силу, с которой Солнце притягивает Землю, то Земля притягивает Солнце с такой же по модулю, но противоположно направленной силой .

При движении тела по плоскости к нему будет приложена сила трения , направленная в сторону, противоположную движению. Это – сила, с которой неподвижная плоскость действует на тело. На основании четвертой аксиомы тело действует на плоскость с такой же силой, но ее направление будет противоположно силе .

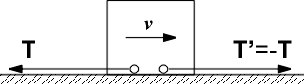
На рис. 1.10 показано тело, движущееся вправо; сила трения приложена к движущемуся телу, а сила  – к плоскости.

Рис. 1.10.

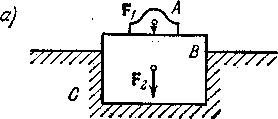
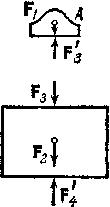
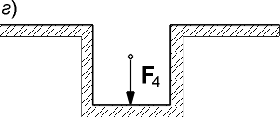
Рассмотрим еще покоящуюся систему, изображенную на рис. 1.11 а. Она состоит из двигателя А, установленного на фундаменте В, который в свою очередь находится на основании С. На двигатель и фундамент действуют силы тяжести и соответственно (они представляют собой действие Земли на эти тела). Кроме указанных двух сил, действуют также следующие силы:  – сила действия тела А на тело В (она равна весу тела А);
	Рис. 1.11.

 – сила обратного действия тела В на тело А;

 – сила действия тел А и В на основание С (она равна суммарному весу тел А и В);

 – сила обратного действия основания С на тело В. Эти силы показаны на рис. 1.11, б, в, г.

Согласно аксиоме 4

, ,

причем эти силы взаимодействия определяются заданными силами и .

Для нахождения сил взаимодействия необходимо исходить из аксиомы 1. Вследствие покоя тела А (рис. 1.11 б) должно быть

,

а значит, .

Точно так же из условия равновесия тела В (рис. 1.11 в) следует

,

т.е.

.

Аксиома 5. Равновесие деформируемого тела не нарушится, если жёстко связать его точки и считать тело абсолютно твердым.

Этой аксиомой (ее называют иногда принципом отвердевания) пользуются в тех случаях, когда речь идет о равновесии тел, которые нельзя считать твердыми. Приложенные к таким телам внешние силы должны удовлетворять условиям равновесия твердого тела, однако для нетвердых тел эти условия являются лишь необходимыми, но не достаточными. Проиллюстрируем это положение простым примером. Было показано, что для равновесия абсолютно твердого невесомого стержня необходимо и

достаточно, чтобы приложенные к концам стержня силы и действовали по прямой, соединяющей его концы, были равны по модулю и направлены в разные стороны.

Рис. 1.12

Эти же условия необходимы и для равновесия отрезка невесомой нити, но для нити они недостаточны – необходимо дополнительно потребовать, чтобы силы, действующие на нить, были растягивающими (рис. 1.12 б), в то время как для стержня они могут быть и сжимающими (рис. 1.12 а).

В заключение этого параграфа рассмотрим случай эквивалентности нулю трех непараллельных сил, приложенных к твердому телу (рис. 1.13 а).

Теорема о трех непараллельных силах. Если под действием трех сил тело находится в равновесии и линии действия двух сил пересекаются, то все силы лежат в одной плоскости и их линии действия пересекаются в одной точке.

Пусть на тело действует система трех сил, , и , причем линии действия сил и пересекаются в точке А (рис. 1.13 а).	а)	б)	в)
	Рис. 1.13.

Согласно следствию из аксиомы 2 силы и можно перенести в точку А (рис. 1.13 б), а по аксиоме 3 их можно заменить одной силой , причем (рис. 1.13 в)

.

Таким образом, рассматриваемая система сил приведена к двум силам и (рис. 1.13,б). По условиям теоремы тело находится в равновесии, следовательно, по аксиоме I силы R и F3 должны иметь общую линию действия, но тогда линии действия всех трех сил должны пересекаться в одной точке.