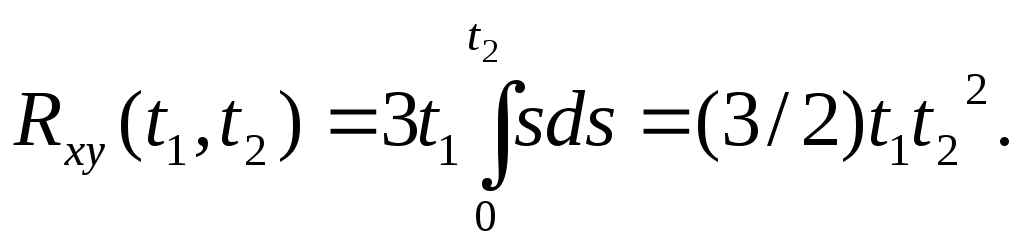§ 17. Интеграл от случайной функции и его характеристики

Интегралом от случайной функции Х(t) по отрезку [0,t] называют предел в среднеквадратическом интегральной суммы при стремлении к нулю частичного интервала Δs_i, максимальной длины (переменная интегрирования обозначена через s, чтобы отличить ее от предела интегрирования t):

Пусть известны характеристики случайной функции. Как найти характеристики интеграла от случайной функции? Ответ на этот вопрос дают теоремы, приведенные ниже.

Теорема 1. Математическое ожидание интеграла от случайной функции равно интегралу от ее математического ожидания:

если

то

Доказательство. По определению интеграла,

Приравняем математические ожидания обеих частей равенства:

Изменим порядок нахождения математического ожидания и предела (законность изменения порядка этих операций примем без доказательства):

Воспользуемся теоремой сложения математических ожиданий:

Учитывая, что —интегральная сумма функции m_x(s), окончательно получим

Замечание. По существу доказано, что операции нахождения математического ожидания и среднеквадратичного интегрирования можно менять местами. Действительно, запишем доказанную теорему так:

Видим, что в левой части равенства сначала находят интеграл, а затем математическое ожидание; в правой части — наоборот.

Пример 1. Зная математическое ожидание m_x(t)=2t+1 случайной функции Х(t), найти математическое ожидание интеграла

Решение. Искомое математическое ожидание

Теорема 2. Корреляционная функция интеграла от случайной функции Х(t) равна двойному интегралу от ее корреляционной функции:

если

,

то

Доказательство. По определению корреляционной функции,

К_y(t₁,t₂)=M[(t₁)(t₂)]

Центрированная случайная функция

или

(*)

Поскольку под знаком определенного интеграла переменную интегрирования можно обозначать любой буквой, обозначим переменную интегрирования в одном интеграле через s₁, а в другом—через s₂, (чтобы отличить переменные интегрирования и пределы интегрирования):

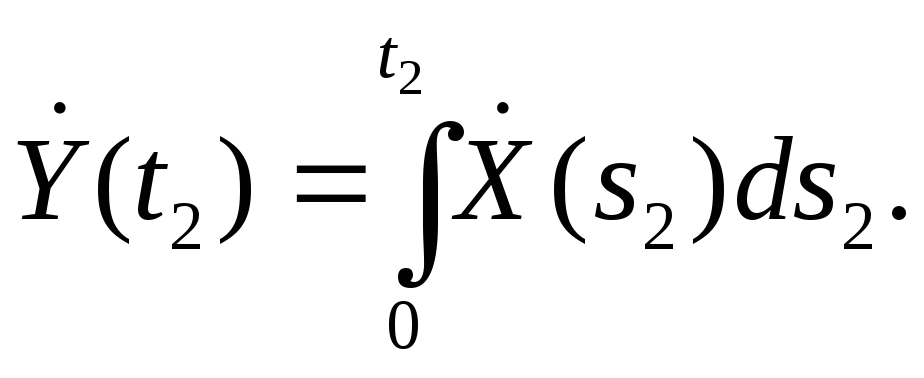
Следовательно,

Приравняем математические ожидания обеих частей равенства:

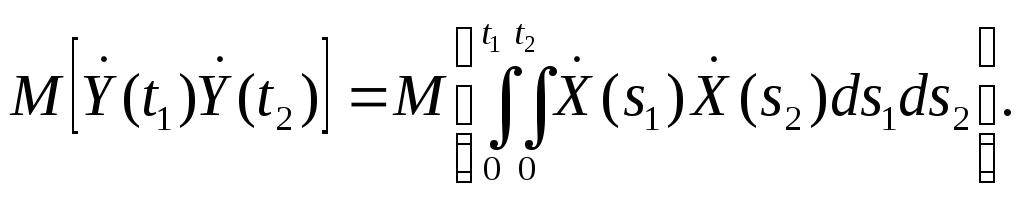
Изменив порядок операций нахождения математического ожидания и интегрирования, окончательно получим

(**)

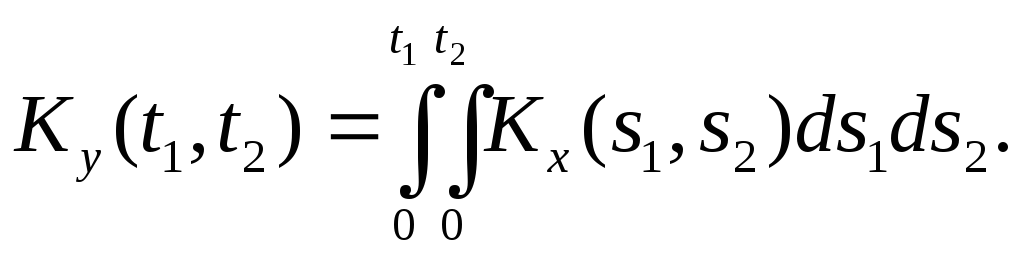Пример 2. Зная корреляционную функцию K_x(t₁,t₂)=4t₁t₂+9t₁²t₂² случайной функции Х(t), найти корреляционную функцию интеграла

Решение. Используя формулу (**), найдем

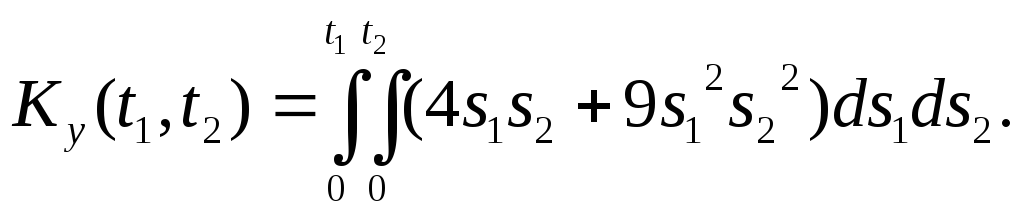
Выполнив интегрирование, получим искомую корреляционную функцию:

Теорема 3.Взаимная корреляционная функция случайной функции X(t) и интеграла равна интегралу от корреляционной функции случайной функции X(t):

a)

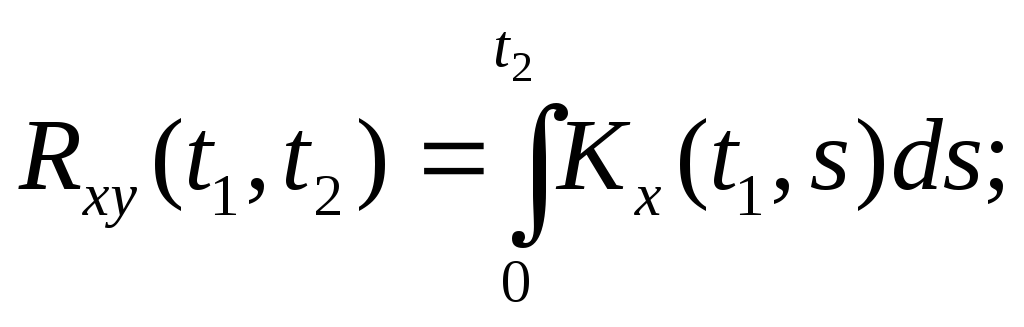
б)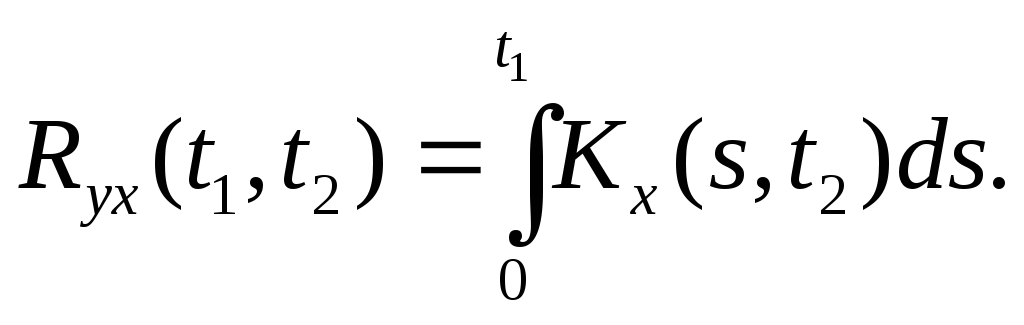

Доказательство. а) По определению взаимной корреляционной функции,

(***)

В силу соотношения (*) центрированная функция

следовательно,

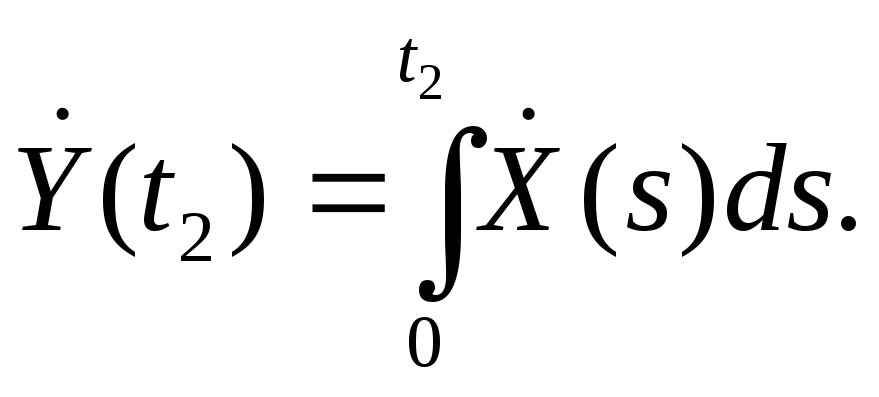
Подставим правую часть этого равенства в (***):

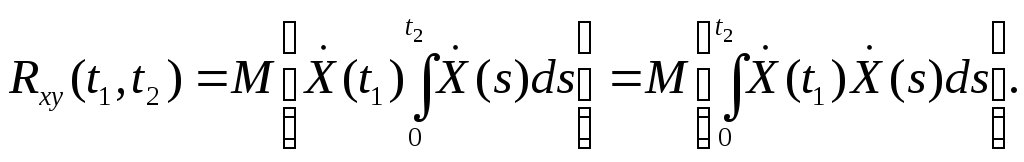
Операции нахождения математического ожидания и интегрирования можно менять местами (см. § 17, замечание), поэтому

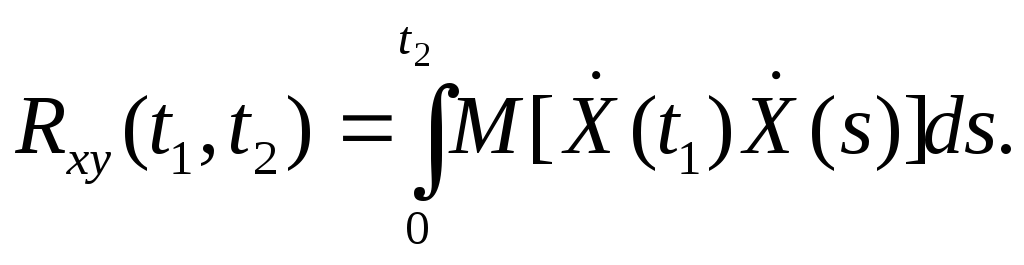
или окончательно

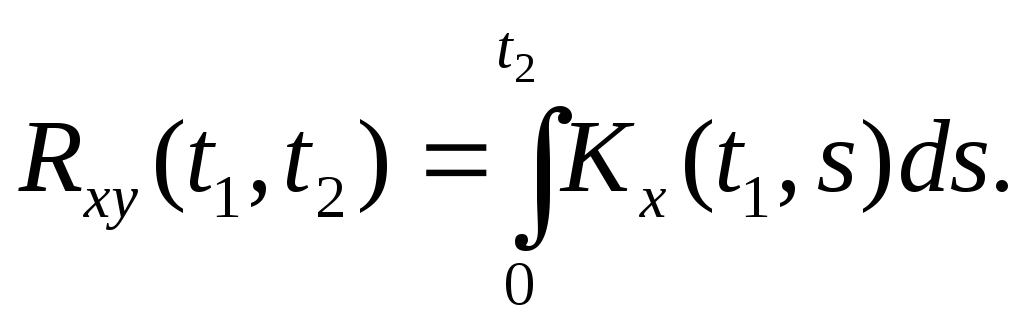
б) Доказывается аналогично.

Пример 3. Задана корреляционная функция К_х(t₁,t₂)=3t₁t₂ X(t). Найти взаимную корреляционную функцию R_xy(t₁,t₂) случайной функции Х(t) и

Решение. Используя формулу

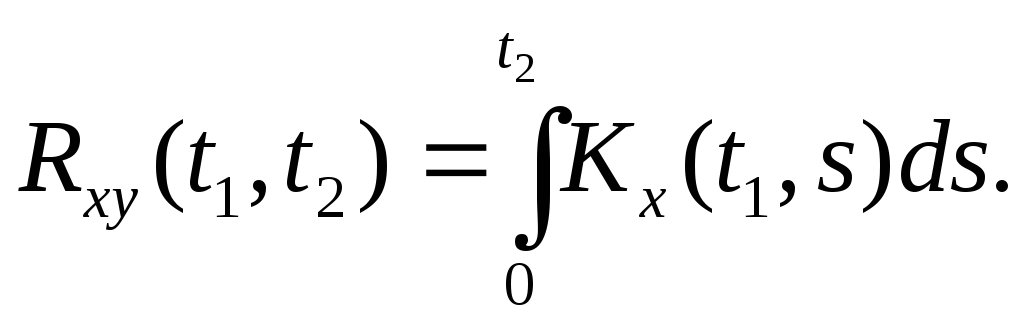
получим искомую корреляционную функцию: