§ 8. Определение характеристик аргодическях стационарных случайных

функций из опыта

Среди стационарных случайных функций можно выделить класс функций, оценка характеристик которых путем усреднения множества реализации равносильна усреднению по времени только одной реализации достаточно большой длительности.

Стационарную случайную функцию X(t) называют аргодической, если ее характеристики, найденные усреднением множества реализации, совпадают с соответствующими характеристиками, полученными усреднением по времени одной реализации x(t), которая наблюдалась на интервале (0,Т) достаточно большой длительности.

Достаточное условие эргодичности стационарной случайной функции Х(t) относительно математического ожидания состоит в том, что ее корреляционная функция k_x(τ) при τ→∞ стремится к нулю:

Достаточное условие эргодичности стационарной случайной функции Х(t) относительно корреляционной функции состоит в том, что корреляционная функция k_y(τ) при τ→∞ стремится к нулю:

где

В качестве оценки математического ожидания эргодической стационарной случайной функции Х(t) по наблюдавшейся на интервале (0,T) реализации x(t) принимают среднее по времени ее значение:

(*)

Известно, что корреляционная функция стационарной случайной функции

Таким образом, оценить k_x(τ) означает оценить математическое ожидание функции поэтому можно воспользоваться соотношением (*), учитывая, что функция определена при t+τ≤T и, следовательно, t≤T - τ.

Итак, в качестве оценки корреляционной функции эргодической стационарной случайной функции принимают

(**)

либо, что равносильно,

(***)

Практически интегралы вычисляют приближенно, например по формуле прямоугольников. С этой целью делят интервал (0,Т) на п частичных интервалов длиной Δt=Т/п; в каждом частичном i-м интервале выбирают одну точку, например его середину t_i. В итоге оценка (*) принимает вид

Учитывая, что Δt=T/n, окончательно получим

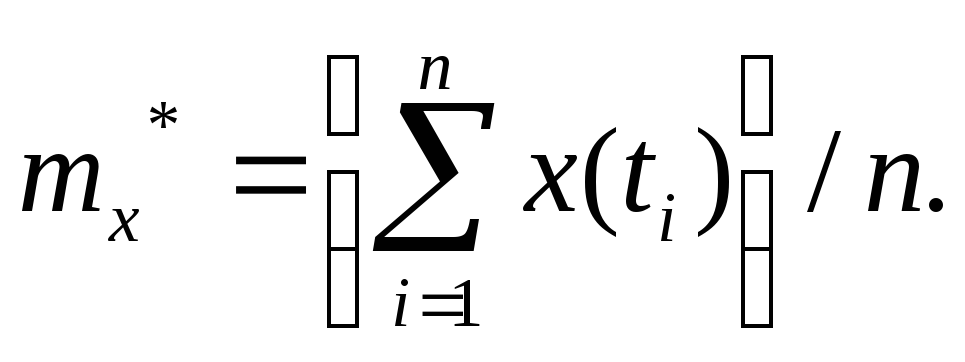
Аналогично приближенно вычисляют интеграл (**), полагая, что τ принимает значения Δt, 2Δt,…,(n-1) Δt, или, что то же, T/n, 2T/n, 3T/n,…,(n-1) T/n.

В итоге оценки корреляционной функции (**) и (***) принимают соответственно вид:

где l= 1, 2, ..., n—1.

Замечание. Можно показать, что оценка (*)—несмещенная, т.е. М[m_x^*]=m_x; оценка (**)—асимптотически несмещенная, т.е.

Задачи

1. Является ли стационарной случайная функция Х(t)=t³U, где U—случайная величина, причем: а)т_и≠0, б) т_и=0?

Отв. а) Нет: т_х(t)≠const; б) Нет: корреляционная функция зависит не от разности аргументов, а от каждого из них.

2. Стационарна ли случайная функция Х(t)=sin(t+φ), гдеφ—случайная величина, распределенная равномерно в интервале (0,2π)?

Отв. Да: т_х(t)=0=const. K_.x(t₁,t₂)=0,5cos(t₂ - t₁).

3. Известно, что если φ—случайная величина, распределенная равномерно в интервале (0,2π), то случайная функция Х(t)=sin(t+φ)—стационарная. Можно ли отсюда непосредственно заключить, что случайная функция Y (t)=cos(t+φ) также стационарна?

Отв. Можно: изменив начало отсчета аргумента, например на π/2, стационарной функции Х(t), получим функцию Y(t).

4. Задана случайная функция Х(t)=t+Usint+Vcost, где U и V—случайные величины, причем М(U)=M(V)=0, D(U)=D (V)=5, M(UV)=0. Доказать, что: а) Х(t)—нестационарная функция; б) X(t)—стационарная функция.

Отв. а) т_х(t)≠const; б) K_x(t₁,t₂)=5cos(t₂ - t₁).

5. Известна корреляционная функция k_x(τ)=стационарной случайной функцииХ(t). Найти корреляционную функцию случайной функции Y(t)=5X(t).

Отв. .

6. Задана корреляционная функция k_x(τ)=стационарной случайной функцииХ(t). Найти нормированную корреляционную функцию.

Отв. .

7. Заданы две стационарные случайные функции Х(t)=cos(2t+φ) и Y(t)=sin(2t+φ), где φ—случайная величина, распределенная равномерно в интервале (0, 2π). Доказать, что заданные функции стационарно связаны.

Отв. R_xy(t₁,t₂)=0,5sin2(t₂ – t₁).

8. Задана корреляционная функция стационарной случайной функцииХ(t). Найти: а) корреляционную функцию; б) дисперсию производной X′(t)=.

Отв. a) ; б) .

9. Задана корреляционная функция стационарной случайной функцииХ(t). Найти взаимные корреляционные функции случайной функции Х(t) и ее производной.

Отв. . ;

10. Задана корреляционная функция стационарной случайной функцииХ(t). Найти дисперсию интеграла .

Отв.D_у(t)=2(t+е^-t - 1).

Глава двадцать пятая

ЭЛЕМЕНТЫ СПЕКТРАЛЬНОЙ ТЕОРИИ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ФУНКЦИЙ