13. .

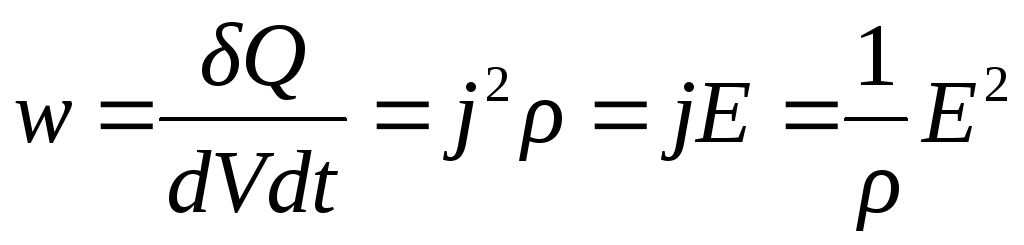14. 1.14. Правила Кирхгофа­­­­

П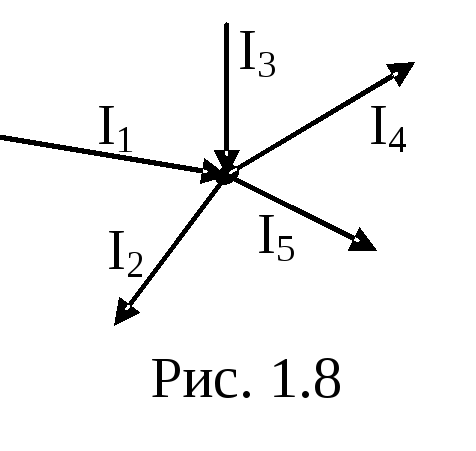ервое правило Кирхгофа(правило узлов) – алгебраическая сумма токов, сходящихся в узле, равна нулю:

,

где n– число проводников, сходящихся в узле,I _k– ток вk-ом проводнике (рис. 1.8).

Положительными считаются токи, подходящие к узлу (токи I₁, I₃), отрицательными – токи, отходящие от узла (токиI₂, I₄, I₅), или наоборот.

Второе правило Кирхгофа(правило контуров) – в любом замкнутом контуре, произвольно выбранном в разветвлённой электрической цепи, алгебраическая сумма напряжений на соответствующих участках этого контура равна алгебраической сумме ЭДС в контуре:

.

Для применения второго правила Кирхгофа выбирается определённое направление обхода контура (по часовой стрелке или против неё). Положительными считаются токи, направления которых совпадает с направлением обхода контура. ЭДС источников считаются положительными, если они создают токи, совпадающие по направлению с направлением обхода контура.

1. Примеры решения задач

1. П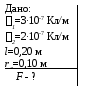рямая бесконечная нить, равномерно заряженная электричеством с линейной плотностью₁ =310^-7 Кл/м, и отрезок длинойl=20 см, равномерно заряженный электричеством с линейной плотностью₂ =210^-7Кл/м, расположены в одной плоскости перпендикулярно друг к другу на расстоянии r₀ = 10 см. Определить силу взаимодействия между ними.

Решение

В задаче рассматривается взаимодействие распределённых зарядов, поэтому для нахождения силы F следует воспользоваться соотношением:

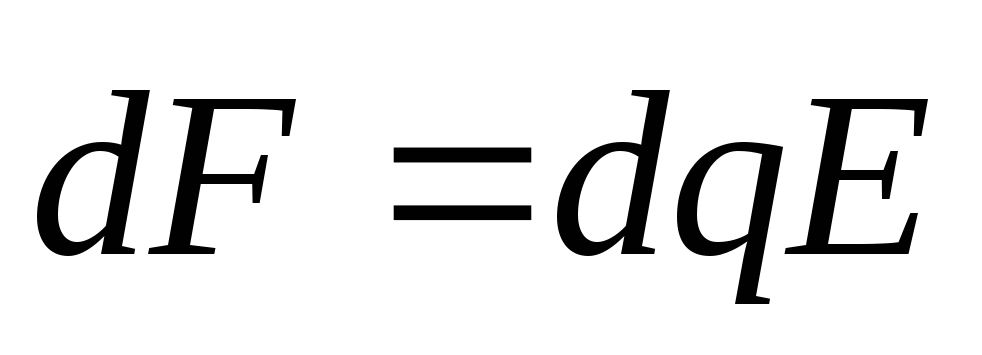. (1)

Нить создаёт вокруг себя электростатическое поле, в котором находится заряд, распределённый на отрезке длиныl. Если выделить на этом отрезке малый участок длинойdr, то находящийся на нём заряд

dq = ₂dr (2)

можно считать точечным и рассматривать dFкак силу, действующую со стороны электрического поля нити наdq. – вектор напряжённости поля нити в месте нахождения электрического зарядаdq. Электрическое поле равномерно заряженной нити определяется выражением

. (3)

Выражение (1) можно переписать в скалярной форме, учитывая, что векторы и параллельны:

dF = Edq. (4)

Подставив (2) и (3) в (4), получим

. (5)

Для нахождения результирующей силы, действующей на отрезок нити с зарядом q₂со стороны поля прямой бесконечной нити, проинтегрируем выражение (5) в пределах от r₀до (r₀+l):

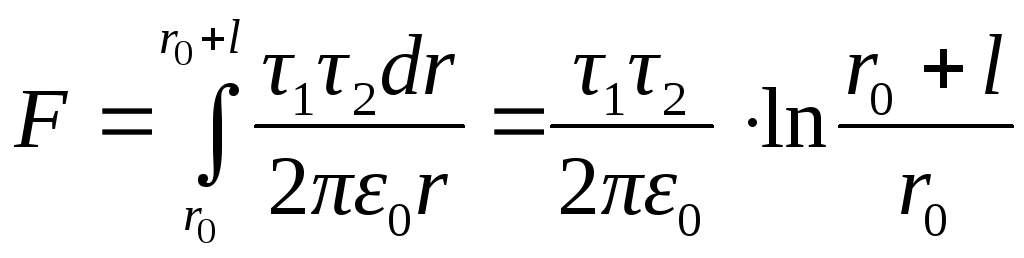. (6)

После подстановки числовых значений получим

.

2. Полый стеклянный шар несёт равномерно распределённый по объёму заряд. Его объёмная плотность =100 нКл/м³. Внутренний радиус шараR₁ =5 см, а наружныйR₂ =10 см. Найти напряжённость электрического поля на расстоянии: а)r₁=3 см; б)r₂ =6 см; в)r₃ =12 см от центра шара.

Решение

Так как заряд шара распределён в пространстве симметрично относительно центра шара О, то и электрическое поле симметрично относительно этой точки. Это позволяет применить для решения задачи метод Гаусса. Из симметрии задачи следует, что вектор направлен вдоль и зависит только от расстояния до центра шара r. Выберем гауссову поверхность в виде сферы, переменного радиусаrс центром в точке О. Учтем, что модуль напряжённости поля шара одинаков во всех точках этой поверхности иЕ _n= E _r. Так как шар диэлектрический, следует применить теорему Гаусса для вектора электрического смещения . Тогда поток вектора смещения сквозь гауссову поверхность

,

где S– площадь гауссовой поверхности,r– её радиус.

Всё пространство можно разбить на 3 области:

1) 0 < r < R₁ 2) R₁ < r < R₂ 3) r > R₂. Применим теорему Гаусса для каждой области.

Для области 0 < r < R₁.

Величина свободного заряда, охватываемого поверхностью интегрирования в пределах первой области, равна нулю. Следовательно, поток вектора смещения также равен нулю, а так как площадь поверхности не нулевая, то смещение и напряжённость поля в пределах первой области равны нулю:

D₁ = 0, Е₁ = D/₀ = 0.

Для области R₁ < r < R₂.

Свободный заряд, охватываемый гауссовой поверхностью, может быть выражен через объём той части шара, которая попала внутрь сферы радиусом r₂:

q _своб = (r₂³-R₁³).

Применяя теорему Гаусса, получим

D₂4r₂² = ,

E₂ = =,

где – диэлектрическая проницаемость стекла.

В/м.

Для области r > R₂.

Внутрь поверхности попадёт весь заряд шара, поэтому

q _своб = (4/3)(R₂³ - R₁³),

и, применив теорему Гаусса, получим выражение

D₃ 4r₃² = (4/3)  (R₂³ - R₁³);

Е ₃ = D ₃/₀ =;

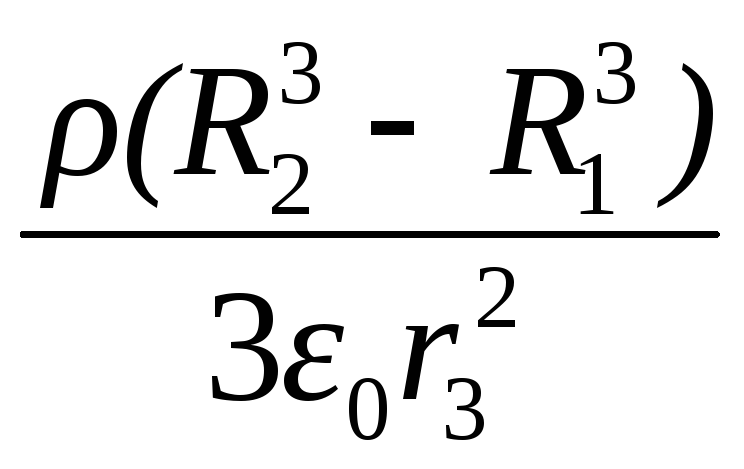В/м.

3. Тонкий стержень согнут в полукольцо. Стержень заряжен с линейной плотностью=133 нКл/м. Какую работу нужно совершить, чтобы перенести зарядq=6,7нКл из центра полукольца в бесконечность?