Метод векторных диаграмм

Этот метод используется для лучшего понимания и наглядности представления процесса, изменяющегося по гармоническому закону.

Суть метода: переменные величины , изменяющиеся по гармоническому закону изображаются графически методом вращающегося вектора амплитуды колебаний.

Для этого из произвольной точки О оси ОXоткладывается вектор, модуль которого равен амплитуде рассматриваемого колебания (рис. 6.5).

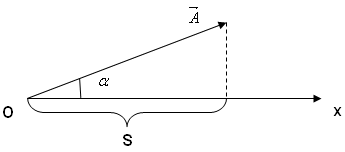
Рис. 6.5. Метод векторных диаграмм

Если вектор привести во вращение относительно точки О против часовой стрелки с циклической частотой, то проекция векторна ось ОХ будет изменяться по закону:

. (6.13)

Таким образом, достигается эквивалентность вращающегося вектора и гармонического закона (6.5).

В общем случае векторная диаграмма – это совокупность вращающихся против часовой стрелки векторов амплитудных (действующих) значений гармонических величин.

Лекция 7. Действующее значение переменного тока. Связь между током и напряжением в элементах электрической цепи тока

Действующее значение переменного тока равно такому значению постоянного тока, которое за время, равное периоду переменного тока, выделяет в том же сопротивлении такое же количество теплоты, что и данный переменный ток.

Для постоянного тока по закону Джоуля-Ленца

, (7.1)

где Q– количество теплоты, выделяемое в проводнике.

Если , тогда, (7.2)

где Т- период переменного тока.

По закону Ома

, тогда. (7.3)

Пусть ток меняется по закону , (7.4)

где – амплитудное значение переменного тока.

Рассмотрим очень малый промежуток времени dt, для которого переменный ток можно считать постоянным (рис. 7.1).

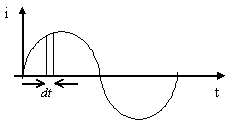
Рис. 7.1. Переменный ток

Тогда по аналогии с выражением (7.3)

, (7.5)

где - количество теплоты, которое выделяется в проводнике за промежуток времени.

Для нахождения количества теплоты, выделяющейся в проводнике за период, проинтегрируем выражение (7.5).

; (7.6)

(7.7)

А в

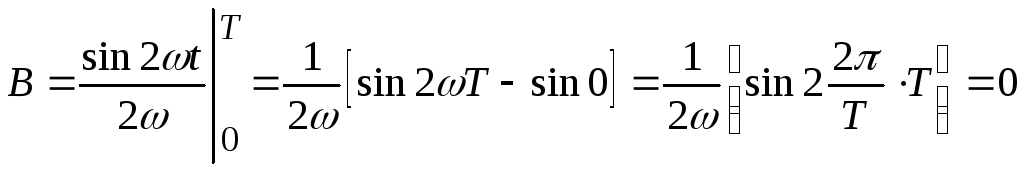. (7.8)

Вывод. Интеграл от периодической знакопеременной функции за 1 период равен 0.

Геометрически это можно трактовать как площадь под кривой периодической функции (рис 7.2).

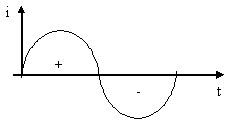
Рис. 7.2. Периодическая функция

Анализируя интеграл А получим:

, т.е.. (7.9)

Сравнивая выражения (7.3) и (7.9) получим:

(7.10)

или , (7.11)

где I– действующее значение переменного тока.

Связь между током и напряжением в элементах электрической цепи

Активное сопротивление

Пусть имеется цепь переменного тока (рис. 7.3).

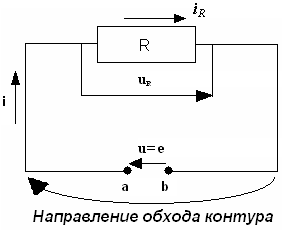
Р

ис. 7.3. Электрическая цепьcактивным сопротивлением

Условия:

1) φ_а > φ_в;

2) напряжение источника в цепи изменяется по закону

. (7.12)

Запишем второй закон Кирхгофа для электрической цепи (рис. 7.3):

u = u_R. (7.13)

По закону Ома , (7.14)

, (7.15)

где – амплитудное значение тока через активное сопротивление, т.е.

. (7.16)

Сравнивая выражения (7.12) и (7.16) заключаем, что на активном сопротивлении ток и напряжение совпадают по фазе (рис. 7.4).

Поделим выражение (7.15) на и получим:

, (7.17)

где и– соответственно действующие значения тока и напряжения на активном сопротивлении.

Закон Ома для действующих значений тока и напряжения на активном сопротивлении:

(7.18)

0 t

0 x

Рис. 7.4. Графики тока и напряжения на активном сопротивлении и векторная диаграмма