Лекция 18. Эдс обмотки якоря

Число полюсов индуктора равно четырем. Вводится р – число пар полюсов. Для этого статора р = 2, а 2р = 4;

Рис. 17.1. Статор двигателя постоянного тока

Рис. 17.2. Полюс

Индукция магнитного поля , (17.1)

где Ф – магнитный поток одного полюса; S – площадь поверхности одного полюса.

; (17.2)

. (17.3)

Найдем ЭДС якоря:

; (17.4)

, (17.5)

где – конструктивная постоянная электрической машины.

Электромагнитный момент, развиваемый в двигателе постоянного тока

Рис. 17.3. Якорь

Так как проводники якоря находятся в магнитном поле, и по ним течет ток, то по закону Ампера на них действует сила. Таким образом, на каждый проводник якоря будет действовать вращающий момент:

; (17.6)

; (17.7)

, (17.8)

где ­– магнитная индукция.

–электромагнитный момент якоря. (17.9)

Назначение пускового сопротивления в схеме двигателе постоянного тока независимого возбуждения

Схема двигателя постоянного тока независимого возбуждения (ДПТ НВ) изображена на рис. 17.4.

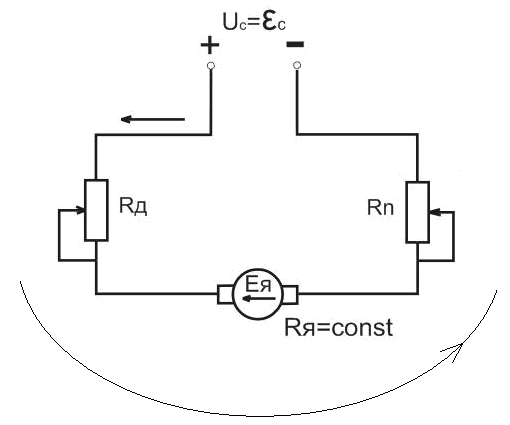
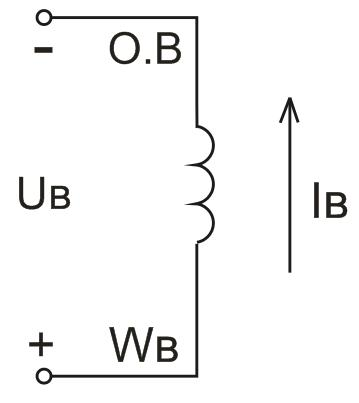
Рис. 17.4. Схема двигателя постоянного тока независимого возбуждения:

W_в – число витков обмотки возбуждения.

По второму закону Кирхгофа для цепи якоря можем записать:

U_с – E_я = R_Д·I_я + R_я·I_Д + R_п·I_я. (17.12)

Предположим, что , тогда

, (17.13)

В момент пуска ω = 0, т.е. Е_я = 0;

–пусковой ток. (17.14)

Пусть ;;

А) ,;

В) ,– приемлемый для эксплуатации ток.

Вывод. Если не принять специальных мер (введение пускового сопротивления в момент пуска), обмотка якоря сгорит, то есть R_П используется для ограничения тока в момент пуска.

При увеличении скорости якоря от ω = 0 до ω = ω_ном ЭДС якоря Е_я увеличивается от 0 до Е_я=U_с и необходимость в R_п пропадает, поэтому R_п рассчитано на кратковременный режим работы – на период пуска. При достижении ω = ω_ном R_п выводится из работы.

Лекция 19. Основные уравнения дпт независимого возбуждения Регулирование скорости двигателя постоянного тока

1. Уравнение баланса напряжений в цепи якоря (см. (17.10) имеет вид

Е_я = U_с – I_я(R_д + R_п + R_я), (18.1)

При работе (R_п= 0) уравнение баланса напряжений в цепи якоря будет иметь вид

Е_я = U_с– I_я(R_д+ R_я). (18.2)

2. Уравнение электромагнитного момента имеет вид М_я= сФI_я. (18.3)

3. Уравнение ЭДС в обмотке якоря имеет вид Е=сФω. (18.4)

4. Закон Ома для магнитной цепи выражается формулой 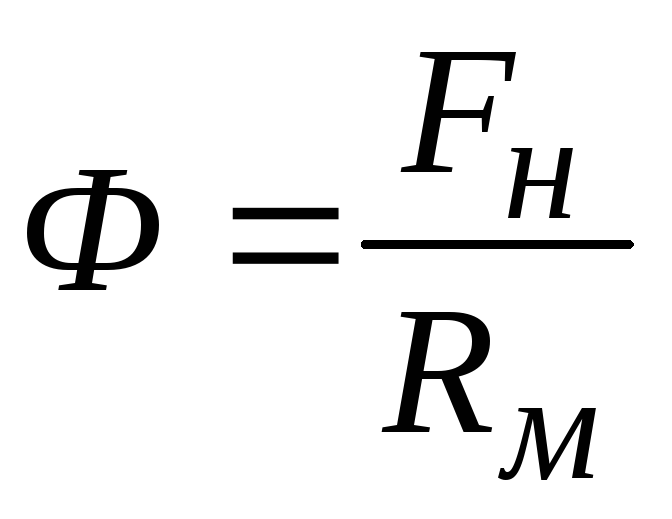, (18.5)

где F_н= W_вI_в (намагничивающая сила обмотки возбуждения); R_м – магнитное сопротивление участка магнитной цепи, по которому замыкается магнитный поток Ф.

. (18.6)

Из выражения (18.4) получим

. (18.7)

Обозначим ;; (18.8–18.9)

; (18.10)

, (18.11)

где иI_я – являются переменными; А и В – коэффициенты.

Следовательно, уравнение , то есть зависимостьявляется прямой линией (рис. 18.1).

Рис.18.1. График функции

В точке В скорость = 0, .

В точке А ток I_я= 0, .

Зависимость (18.11) и рис. (18.1) представляют собой электромеханическую характеристику двигателя постоянного тока независимого возбуждения, т.к. – механическая величина, аI_Я – электрическая величина.

Из уравнения (18.10) видно, что скорость ДПТ можно изменять:

1) путем изменения U_С, такое регулирование скорости называется якорным регулированием.

2) путем изменения магнитного потока Ф, такое регулирование скорости называется полюсное регулирование.

3) путем изменения добавочного сопротивления R_Д – реостатное регулирование.

Рассмотрим подробнее эти способы.