12. Плоские укладки графов, планарные графы, критерий Понтрягина-Куратовского.

Определение. Графом G называется пара (V, E), где – непустое множество вершин графа, а– множество ребер графа, причем каждое ребро – это неупорядоченная пара различных вершин.

Всякий граф можно изобразить на плоскости в виде точек и непрерывных линий, соединяющих эти точки. При этом один и тот же граф может иметь бесконечно много различных изображений (укладок графа на плоскости).

Определение. Изображение графа на плоскости без внутренних точек пересечения ребер называется плоской укладкой графа.

Определение. Граф называется планарным, если существует его плоская укладка.

Утверждение 1 (необходимое условие планарности). Для любого связного планарного графа с n вершинами и m ребрами, где n ≥ 3, выполняется неравенство .

Утверждение 2 (необходимое условие планарности). В любом планарном графе есть вершина, степень которой не превосходит пяти.

Определение. Два графа называются гомеоморфными, если их можно получить из одного графа с помощью однократного или многократного применения операции подразбиения ребра. Критерий планарности (критерий Понрягина-Куратовского). Граф планарен тогда и только тогда, когда в нем нет подграфов, гомеоморфных графу К5 или К3,3.

K3,3 K5

13. Необходимые условия планарности, формула Эйлера для планарных графов.

Определение. Графом G называется пара (V, E), где 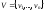– непустое множество вершин графа, а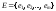– множество ребер графа, причем каждое ребро – это неупорядоченная пара различных вершин.

Всякий граф можно изобразить на плоскости в виде точек и непрерывных линий, соединяющих эти точки. При этом один и тот же граф может иметь бесконечно много различных изображений (укладок графа на плоскости).

Определение. Изображение графа на плоскости без внутренних точек пересечения ребер называется плоской укладкой графа.

Определение. Граф называется планарным, если существует его плоская укладка.

Утверждение 1 (необходимое условие планарности). Для любого связного планарного графа с n вершинами и m ребрами, где n ≥ 3, выполняется неравенство .

Утверждение 2 (необходимое условие планарности). В любом планарном графе есть вершина, степень которой не превосходит пяти.

Определение. Говорят, что граф состоит изkкомпонент связности, если его можно представить как объединениеkсвязных графов, не имеющих общих вершин.

Формула Эйлера. Для всякого планарного графа справедлива формула Эйлера: 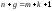, гдеn– количество вершин,g– граней,m– ребер,k– компонент связности в исходном графе. Под гранями здесь понимаются связные области, на которые распадается плоскость, если провести «разрезы» по всем ребрам плоской укладки графа. Для связного планарного графа формулу Эйлера можно записать иначе:.

14. Правильные вершинные раскраски графов, хроматическое число, неравенства для хроматического числа.

Определение. Графом G называется пара (V, E), где – непустое множество вершин графа, а– множество ребер графа, причем каждое ребро – это неупорядоченная пара различных вершин.

Определение. Говорят, что вершины графа G правильно раскрашены с помощью цветов {c₁, c₂,…, c_r}, если каждой вершине поставлен в соответствие некоторый цвет, причем любым двум смежным вершинам соответствуют разные цвета.

Утверждение 1. Для правильной раскраски вершин любого двудольного графа достаточно двух цветов.

Определение. Хроматическим числом графа называется минимальное число красок, достаточное для правильной раскраски его вершин.

Хроматическое число графа G далее будем обозначать через χ(G). Выполняются следующие свойства хроматического числа:

1. ;

2. если G – двудольный граф, то ;

3. если Т – дерево, то (так как всякое дерево – двудольный граф);

4. если G – планарный граф, то .

Утверждение 2. Для любого графа G справедлива верхняя оценка , гдеd = max deg(v).

Определение. Хроматическим многочленом графа G называется многочлен P(G,x), который при каждом целом неотрицательном значении х равен количеству различных способов правильной раскраски вершин графа G с использованием не более х фиксированных цветов.