3. Основные операции над графами, неравенства для числа вершин, ребер и компонент связности графа.

Графом Gназывается пара (V,E), где– непустое множество вершин графа, а– множество ребер графа, причем каждое ребро – это неупорядоченная пара различных вершин.

Утверждение. Если в графе количество вершинn≥ 2, то в нем найдутся хотя бы две вершины с одинаковой степенью.

Утверждение. Для любого графаG= (V,E) сnвершинами иmребрами справедливо равенство т.е. сумма степеней всех вершин графа равна удвоенному количеству ребер.

К графам или отдельным его элементам могут применяться следующие операции:

• добавление ребра, соединяющего две несмежные вершины;

• удаление ребра (концы ребра сохраняются);

• добавление вершины;

• удаление вершины (вместе с инцидентными ей ребрами);

• отождествление двух несмежных вершин (все ребра, инцидентные отождествляемым вершинам, сохраняются и становятся инцидентными полученной вершине; если при этом возникают кратные ребра, они заменяются одним ребром);

• подразбиение ребра [u,v] (сначала добавляются новая вершина w и новые ребра [u,w], [w,v], затем удаляется ребро [u,v]);

• стягивание ребра [u,v] (сначала удаляется ребро [u,v], а затем вершины u и v отождествляются);

• объединение графов и(в результате получается графU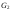, вершинами и ребрами которого являются вершины и ребра графови).

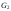Определение. Граф называется связным, если в нем любые две вершины соединены цепью.

Определение. Говорят, что граф состоит изkкомпонент связности, если его можно представить как объединениеkсвязных графов, не имеющих общих вершин.

Определение. Мостом в графе называется ребро, при удалении которого увеличивается количество компонент связности этого графа.

Утверждение 1. Количество реберmв любом связномn-вершинном графе удовлетворяет неравенствам.

Утверждение 2. Еслиn-вершинный граф состоит изkкомпонент связности, то количество его реберmудовлетворяет неравенствам.

4. Типы графов, дополнительные графы, двудольные графы, критерий двудольности.

Графом G называется пара (V, E), где – непустое множество вершин графа, а– множество ребер графа, причем каждое ребро – это неупорядоченная пара различных вершин.

Определение. Полный n-вершинный граф (клика) – это граф, в котором любые две вершины соединены ребром (обозначается );

Определение. Нулевой n-вершинный граф – это граф без ребер (обозначается );

Определение. Граф называется связным, если в нем любые две вершины соединены цепью.

Определение. Двудольный граф – это граф, множество вершин которого можно так разбить на два непересекающихся подмножества (доли) и, что никакие две вершины из одной доли не смежны;

Утверждение. Критерий двудольности графа - необходимо и достаточно, чтобы в этом графе все циклы имели четную длину.

Определение. Полный двудольный граф – это двудольный граф, в котором каждая вершина из доли смежна каждой вершине из доли(обозначается, гдеn, m – количество вершин в и).

Определение. Дополнительным графом к n-вершинному графу называется графс тем же множеством вершин, не имеющий с графомобщих ребер, и такой, чтоU.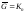

5. Обходы графов: эйлеровы цепи и циклы, необходимые и достаточные условия их существования, алгоритм Флери.

Графом G называется пара (V, E), где – непустое множество вершин графа, а– множество ребер графа, причем каждое ребро – это неупорядоченная пара различных вершин.

Определение. Эйлерова цепь – цепь, подразумевающая обход всех вершин через единичное прохождение каждого ребра, но не подразумевающая возврат в изначальную точку.

Определение. Эйлеров цикл – цикл, при котором происходит обход всех вершин через единичное прохождение каждого ребра.

Утверждение. Критерий существования эйлерова цикла - только тогда, когда в графе все вершины имеют четную степень; связность.

Утверждение. Критерии существования эйлеровой цепи - существует тогда и только тогда, когда в графе ровно две вершины имеют четную степень; связность.

Граф, в котором существует эйлеров цикл, называется эйлеровым графом. Существует алгоритм Флери для построения эйлерового цикла в эйлеровом графе. Этот алгоритм нумерует ребра графа в порядке их прохождения, а сам порядок определяется следующей схемой:

• Из произвольной начальной вершины по любому инцидентному ей ребру переходим в следующую вершину, нумеруем это ребро цифрой 1 и удаляем его.

• Если очередной вершине инцидентно только одно ребро, то переходим по нему в следующую вершину, нумеруем это ребро очередным числом и удаляем его. Если же очередной вершине инцидентны несколько ребер, то среди них обязательно найдется ребро, которое не является мостом в оставшемся графе. По этому ребру переходим в следующую вершину, нумеруем это ребро очередным числом и удаляем его. Этот этап повторяется до тех пор, пока не удалим все ребра графа.

Алгоритм заканчивает работу за конечное число шагов, равное количеству ребер в исходном графе. При этом номера ребер указывают, в каком порядке следуют ребра в эйлеровом цикле.