44. Слова и языки, операции над ними, их свойства.

Определение.Входное слово – произвольная строка конечной длины, составленная из символов входного алфавита А. У таких автоматов одно или несколько состоя­ний заранее объявляются заключительными. Считается, что автомат распознал слово, поданное ему на вход, тогда и только тогда, когда он завершил работу над этим словом в одном из своих заключительных состояний.

Определение.Язык – множество всех слов, распознаваемых автоматом. Сам язык может быть как конечным, так и бесконечным, но в любом случае он состоит только из слов, распознаваемых соответствующим автоматом.

Определение.Суммой языковLиL´называется язык, который обозначаетсяL+L´и получается объединением множествLиL´, т.е.L+L´ =.

Определение.Произведением языковLиL´называется язык, который обозначаетсяL·L´ и получается в результате конкатенации всех возможных словwиw´, гдеwпринадлежит языкуL, аw´– языкуL´, т.е.L·L´ =.

Заметим, что язык L·L´, как правило, отличается от языкаL´·L, хотя некоторые слова могут принадлежать обоим произведениям.

Определение.Итерацией языкаLназывается язык, который обозначаетсяL* и получается в результате сложения бесконечного числа языков {Λ} +L+L²+L³+ … +L^k+ …, т.е.L* =

Итерация выражается через операции сложения и умножения языков. Из всех введенных операций над языками она единственная, которая позволяет из конечного языка получить бесконечный.

Таким образом, с помощью введенных операций сложения, умножения и итерации некоторые языки можно выражать в виде формул через более простые языки. Причем результатом сложения или умножения двух конечных языков всегда будет конечный язык, и лишь итерация позволяет из конечного языка получить бесконечный. Некоторые важные свойства операций над языками:

1. L1· (L2+L3) =L1·L2+L1·L3;	5. L·Λ=L;
2. (L1+L2) ·L3=L1·L3+L2·L3;	6. L·L* =L*·L;
3. L+L=L;	7. Λ+L·L* =L*;
4. L+L* =L*;	8. ((L1)*· (L2)*)* = (L1+L2)*.

Пустое подмножество множества А*, как и всякое другое его подмножество, тоже считается языком. Этот язык мы будем называть пустым языком и обозначать символом пустого множества . Очевидно, что для любого языкаLверны равенстваL+=LиL·=. Значит, при всех натуральных значенияхnвыполняетсяⁿ=. Тогда из определения операции итерации получаем* =Λ++²+³+ … +ⁿ+ … =Λ.

Заметим также, что Λ* = Λ, поскольку Λⁿ = Λ и Λ + Λ = Λ.

Определение.Пусть имеется алфавит А = {а₁, а₂, …, а_s}. Одноэлементные языки а₁, а₂, …, а_s, а также язык, содержащий только пустое словоΛ- элементарные языки.

45. Регулярные выражения и регулярные языки, теорема Клини.

Определение.Регулярным языком называется такой язык, который можно получить из элементарных языков с помощью конечного числа операций сложения, умножения и итерации.

Чтобы доказать регулярность какого-либо языка, надо записать его в виде так называемого регулярного выражения, т.е. формулы, в которой конечное число раз используются элементарные языки и знаки операций сложения, умножения и итерации. Поскольку количество регулярных выражений счетно, то число различных регулярных языков не более, чем счетно. Всего же имеется континуум языков над фиксированным конечным алфавитом А, т.к. язык – это любое подмножество счетного множества А*. Следовательно, существуют и нерегулярные языки.

Пример.Рассмотрим несколько языков.

1. Конечный язык L₁ = {a, ab, abc} является регулярным языком, т.к. его можно задать равенством L₁ = a + ab + abc = a + a·b + a·b·c = a·(Λ + b·(Λ + c)). Последнее полученное выражение является регулярным, поскольку оно содержит только простейшие языки a, b, c и Λ и конечное число знаков операций сложения и умножения. Этот пример показывает, что любое конечное множество слов образует регулярный язык.

2. Бесконечный язык L₂ = {с, cabc, cabcabc, cabcabcabc, …}, порождаемый автоматом из примера 4 §3, является регулярным, т.к. его можно задать разными регулярными выражениями: с·(a·b·с)*, либо (с·a·b)*·с. Этот пример свидетельствует о том, что один и тот же язык можно представить через различные регулярные выражения.

3. Бесконечный язык L₃, состоящий из всех слов конечной длины в алфавите А = {a, b, c}, включая и пустое слово, является регулярным языком, поскольку выполняется равенство L₃ = (a + b + с)*.

4. Бесконечный язык L₄ над алфавитом А = {a, b, c}, образованный словами, которые содержат хотя бы одну букву с, регулярен, т.к. он может быть задан равенством L₄ = (a + b + с)*· с· (a + b + с)*.

5. Бесконечный язык L₅ над алфавитом А = {0,1}, образованный всеми словами, кроме слов 0 и 11, регулярен, т.к. его можно задать регулярным выражением Λ + 1 + 00 + 01 + 10 + (0 + 1)³ · (0 + 1)*.

6. Бесконечный язык L₆ = {1, 10, 101, 1010, 10100, …}, состоящий из всех начальных отрезков {а₁, а₁а₂, а₁а₂а₃, …} бесконечной последовательности (10100100010…), не является регулярным.

Определение.Пересечением языковLиL´называется язык, который обозначаетсяL∩L´ и состоит из всех слов, принадлежащих одновременно обоим языкамLиL´. Поскольку всякий язык является подмножеством множества А* всех слов конечной длины в некотором фиксированном алфавите А, то пересечение языков – это обычная операция пересечения множеств слов.

Определение.Дополнением языкаLв алфавите А называется язык, который обозначаетсяи состоит из слов множества А*, не принадлежащих языкуL. ЯзыкLи его дополнениене имеют общих слов, а их сумма совпадает с множеством А*. Операция пересечения языков не относится к числу основных, поскольку она может быть выражена через операции сложения и дополнения. Действительно, из закона де Моргана следует, что.

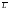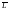Пример.Пусть исходный языкLсостоит из всех таких слов в алфавите А = {0,1}, которые начинаются с нуля, а оканчиваются двумя единицами. Нетрудно проверить, что этот язык можно задать регулярным выражением 0· (0 + 1)*· 11. Тогда дополнительный к нему языксостоит из всех таких слов в алфавите А, которые начинаются с единицы или оканчиваются любой из трех комбинаций – 00, 01 или 10. Языкможно задать регулярным выражением 1· (0 + 1)* + (0 + 1)*· (0· 0+ 0· 1 + 1· 0).

При фиксированном алфавите А класс регулярных языков над А замкнут относительно всех перечисленных выше операций – сложения, умножения, итерации, пересечения и дополнения. Это означает, что язык, получаемый в результате применения данных операций к регулярным языкам, тоже является регулярным.

Существует тесная связь между регулярными языками и конечными автоматами. Дело в том, что, с одной стороны, любой регулярный язык обязательно распознается некоторым конечным детерминированным автоматом (автоматом Мили). А с другой стороны, автоматы Мили способны распознавать только регулярные языки. Оба эти утверждения сформулированы в основной теореме теории автоматов (теореме Клини).

Теорема Клини.ЯзыкLраспознается конечным детерминированным автоматом тогда и только тогда, когдаL– регулярный язык.