- •1. Основные понятия теории графов, удаленность вершины, центр, радиус и диаметр графа.
- •2. Способы задания графов, свойства матриц смежности и инциденций, теорема о рукопожатиях.
- •3. Основные операции над графами, неравенства для числа вершин, ребер и компонент связности графа.
- •4. Типы графов, дополнительные графы, двудольные графы, критерий двудольности.
- •5. Обходы графов: эйлеровы цепи и циклы, необходимые и достаточные условия их существования, алгоритм Флери.
- •6. Обходы графов: гамильтоновы цепи и циклы, достаточные условия их существования.
- •7. Деревья, их свойства, кодирование деревьев, остовные деревья.
- •8. Экстремальные задачи теории графов: минимальное остовное дерево, алгоритмы Прима и Краскала.
- •9. Экстремальные задачи теории графов: задача коммивояжера, «жадный» алгоритм
- •10. Экстремальные задачи теории графов: задача о кратчайшем пути, алгоритм Дейкстры.
- •11. Изоморфизм и гомеоморфизм графов, методы доказательства изоморфности и неизоморфности графов.
- •12. Плоские укладки графов, планарные графы, критерий Понтрягина-Куратовского.
- •13. Необходимые условия планарности, формула Эйлера для планарных графов.
- •14. Правильные вершинные раскраски графов, хроматическое число, неравенства для хроматического числа.
- •15. Теорема о пяти красках, гипотеза четырех красок, «жадный» алгоритм.
- •16. Хроматический многочлен, его нахождение и свойства.
- •17. Задача о поиске выхода из лабиринта, реберная раскраска графа.
- •18. Ориентированные графы, источники и стоки, топологическая сортировка, алгоритм Демукрона.
- •19. Составление расписания выполнения комплекса работ в кратчайшие сроки методами теории графов.
- •20. Элементарные булевы функции и способы их задания (табличный, векторный, формульный, графический, карта Карно).
- •21. Существенные и фиктивные переменные булевых функций, основные тождества, эквивалентные преобразования формул.
- •22. Линейные и нелинейные полиномы Жегалкина, разложение булевых функций в полином Жегалкина методом неопределенных коэффициентов.
- •23. Линейные и нелинейные полиномы Жегалкина, разложение булевых функций в полином Жегалкина методом эквивалентных преобразований.
- •24. Разложение булевых функций в сднф и скнф.
- •25. Минимизация днф и кнф методом эквивалентных преобразований.
- •26. Минимизация днф и кнф с помощью карт Карно.
- •27. Замкнутые классы булевых функций т0, т1, l, лемма о нелинейной функции.
- •28. Замкнутые классы булевых функций s и м, леммы о несамодвойственной и немонотонной функции.
- •29. Полная система функций, теорема о двух системах булевых функций.
- •30. Теорема Поста о полноте системы булевых функций, алгоритм проверки системы на полноту, базис.
- •31. Схемы из функциональных элементов, правила построения и функционирования, метод синтеза сфэ, основанный на сднф и скнф.
- •32. Метод синтеза сфэ, основанный на компактной реализации всех конъюнкций с помощью универсального многополюсника, сложность получаемых схем.
- •33. Основные комбинаторные операции, сочетания и размещения (с возвращением и без возвращения элементов).
- •34. Комбинаторные принципы сложения, умножения, дополнения, включения-исключения.
- •35. Биномиальные коэффициенты, их свойства, бином Ньютона.
- •36. Треугольник Паскаля, полиномиальная формула.
- •37. Алфавитное кодирование: необходимое и достаточные условия однозначности декодирования.
- •38. Алфавитное кодирование: теорема Маркова, алгоритм Маркова.
- •39. Коды с минимальной избыточностью (коды Хаффмана), метод построения.
- •40. Линейные коды, порождающая матрица, двойственный код.
- •41. Самокорректирующиеся коды (коды Хэмминга), метод построения.
- •42. Определение, схема и функционирование абстрактного автомата, способы задания автоматов.
- •43. Типы конечных автоматов, автоматы Мили и Мура, автоматы-генераторы.
- •44. Слова и языки, операции над ними, их свойства.
- •45. Регулярные выражения и регулярные языки, теорема Клини.
- •46. Задача анализа автоматов-распознавателей.
- •47. Задача синтеза автоматов-распознавателей.
- •48. Эквивалентные состояния автомата-распознавателя, эквивалентные автоматы-распознаватели, минимизация автоматов-распознавателей, алгоритм Мили.
- •49. Эквивалентные состояния автомата-преобразователя, эквивалентные автоматы- преобразователи, минимизация автоматов- преобразователей, алгоритм Мили.
- •50. Детерминированные и недетерминированные функции, примеры, способы задания.
- •51. Ограниченно-детерминированные (автоматные) функции, способы их задания.
- •52. Логические автоматы, способы их задания, синтез двоичного сумматора.
- •53. Операции над логическими автоматами: суперпозиция и введение обратной связи.
Дискретная математика
Оглавлени
Дискретная математика 1
Теория графов 3
1. Основные понятия теории графов, удаленность вершины, центр, радиус и диаметр графа. 3
2. Способы задания графов, свойства матриц смежности и инциденций, теорема о рукопожатиях. 3
3. Основные операции над графами, неравенства для числа вершин, ребер и компонент связности графа. 4
4. Типы графов, дополнительные графы, двудольные графы, критерий двудольности. 5
5. Обходы графов: эйлеровы цепи и циклы, необходимые и достаточные условия их существования, алгоритм Флери. 5
6. Обходы графов: гамильтоновы цепи и циклы, достаточные условия их существования. 5
7. Деревья, их свойства, кодирование деревьев, остовные деревья. 6
8. Экстремальные задачи теории графов: минимальное остовное дерево, алгоритмы Прима и Краскала. 6
9. Экстремальные задачи теории графов: задача коммивояжера, «жадный» алгоритм 7
10. Экстремальные задачи теории графов: задача о кратчайшем пути, алгоритм Дейкстры. 7
11. Изоморфизм и гомеоморфизм графов, методы доказательства изоморфности и неизоморфности графов. 7
12. Плоские укладки графов, планарные графы, критерий Понтрягина-Куратовского. 8
13. Необходимые условия планарности, формула Эйлера для планарных графов. 8
14. Правильные вершинные раскраски графов, хроматическое число, неравенства для хроматического числа. 8
15. Теорема о пяти красках, гипотеза четырех красок, «жадный» алгоритм. 9
16. Хроматический многочлен, его нахождение и свойства. 9
17. Задача о поиске выхода из лабиринта, реберная раскраска графа. 10
18. Ориентированные графы, источники и стоки, топологическая сортировка, алгоритм Демукрона. 10
19. Составление расписания выполнения комплекса работ в кратчайшие сроки методами теории графов. 10
Теория булевой алгебры 11
20. Элементарные булевы функции и способы их задания (табличный, векторный, формульный, графический, карта Карно). 11
21. Существенные и фиктивные переменные булевых функций, основные тождества, эквивалентные преобразования формул. 12
22. Линейные и нелинейные полиномы Жегалкина, разложение булевых функций в полином Жегалкина методом неопределенных коэффициентов. 13
23. Линейные и нелинейные полиномы Жегалкина, разложение булевых функций в полином Жегалкина методом эквивалентных преобразований. 13
24. Разложение булевых функций в СДНФ и СКНФ. 14
25. Минимизация ДНФ и КНФ методом эквивалентных преобразований. 14
26. Минимизация ДНФ и КНФ с помощью карт Карно. 15
27. Замкнутые классы булевых функций Т0, Т1, L, лемма о нелинейной функции. 15
28. Замкнутые классы булевых функций S и М, леммы о несамодвойственной и немонотонной функции. 16
29. Полная система функций, теорема о двух системах булевых функций. 16
30. Теорема Поста о полноте системы булевых функций, алгоритм проверки системы на полноту, базис. 17
31. Схемы из функциональных элементов, правила построения и функционирования, метод синтеза СФЭ, основанный на СДНФ и СКНФ. 17
32. Метод синтеза СФЭ, основанный на компактной реализации всех конъюнкций с помощью универсального многополюсника, сложность получаемых схем. 17
Элементы комбинаторики 18
33. Основные комбинаторные операции, сочетания и размещения (с возвращением и без возвращения элементов). 18
34. Комбинаторные принципы сложения, умножения, дополнения, включения-исключения. 19
35. Биномиальные коэффициенты, их свойства, бином Ньютона. 19
36. Треугольник Паскаля, полиномиальная формула. 19
Теория кодирования 20
37. Алфавитное кодирование: необходимое и достаточные условия однозначности декодирования. 20
38. Алфавитное кодирование: теорема Маркова, алгоритм Маркова. 21
39. Коды с минимальной избыточностью (коды Хаффмана), метод построения. 22
40. Линейные коды, порождающая матрица, двойственный код. 23
41. Самокорректирующиеся коды (коды Хэмминга), метод построения. 23
Теория автоматов 24
42. Определение, схема и функционирование абстрактного автомата, способы задания автоматов. 24
43. Типы конечных автоматов, автоматы Мили и Мура, автоматы-генераторы. 26
44. Слова и языки, операции над ними, их свойства. 26
45. Регулярные выражения и регулярные языки, теорема Клини. 27
46. Задача анализа автоматов-распознавателей. 28
47. Задача синтеза автоматов-распознавателей. 29
48. Эквивалентные состояния автомата-распознавателя, эквивалентные автоматы-распознаватели, минимизация автоматов-распознавателей, алгоритм Мили. 31
49. Эквивалентные состояния автомата-преобразователя, эквивалентные автоматы- преобразователи, минимизация автоматов- преобразователей, алгоритм Мили. 33
50. Детерминированные и недетерминированные функции, примеры, способы задания. 33
51. Ограниченно-детерминированные (автоматные) функции, способы их задания. 34
52. Логические автоматы, способы их задания, синтез двоичного сумматора. 35
53. Операции над логическими автоматами: суперпозиция и введение обратной связи. 36
Теория графов
1. Основные понятия теории графов, удаленность вершины, центр, радиус и диаметр графа.
Графом
Gназывается пара (V,E),
где – непустое множество вершин графа, а
– непустое множество вершин графа, а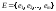 – множество ребер графа, причем каждое
ребро – это неупорядоченная пара
различных вершин.
– множество ребер графа, причем каждое
ребро – это неупорядоченная пара
различных вершин.
|
Пусть ребро е соединяет вершины uиv. В этом случае пишутe= [u,v] и говорят, что
Определение. Степенью вершины называется количество инцидентных ей ребер. Определение. Вершина называется изолированной, если она не инцидентна ни одному ребру; вершина называется концевой, если ей инцидентно только одно ребро. |
Рис.1 |
Утверждение. Если в графе количество вершинn≥ 2, то в нем найдутся хотя бы две вершины с одинаковой степенью.
Утверждение. Для любого графаG= (V,E) сnвершинами иmребрами справедливо равенство т.е. сумма степеней всех вершин графа равна удвоенному количеству ребер.
Определение.
Последовательность ребер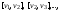
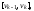
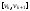 ,
в которой все ребра различны, называется
цепью длиныk, соединяющей
вершины
,
в которой все ребра различны, называется
цепью длиныk, соединяющей
вершины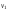 и
и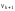 .
При этом вершины
.
При этом вершины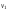 и
и называются концами цепи.
называются концами цепи.
Определение.
Расстоянием между вершинамиuиvназывается число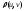 ,
равное длине кратчайшей цепи, соединяющей
вершиныuиv.
,
равное длине кратчайшей цепи, соединяющей
вершиныuиv.
Определение.
Эксцентриситетом вершиныuназывается число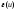 ,
равное максимальному расстоянию от
вершиныuдо остальных
вершин графа, т.е.
,
равное максимальному расстоянию от
вершиныuдо остальных
вершин графа, т.е.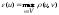 .
.
Определение.
Радиусом графаGназывается
числоr(G),
равное минимальному эксцентриситету
его вершин, т.е. .
.
Определение.
Диаметром графаGназывается
числоd(G),
равное максимальному эксцентриситету
его вершин, т.е. .
.
Известно,
что для любого графа Gвыполняется соотношение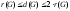 .
.
Определение. Центром графаGназывается множество его вершин, имеющих минимальный эксцентриситет.
|
Пример 2. Рассмотрим графG, изображенный на рис.2. Эксцентриситеты его вершин:
Следовательно,
его радиус и диаметр r(G) = 2,d(G) = 4,
а центр – вершина |
Рис.2 |
2. Способы задания графов, свойства матриц смежности и инциденций, теорема о рукопожатиях.
Графом
Gназывается пара (V,E),
где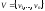 – непустое множество вершин графа, а
– непустое множество вершин графа, а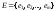 – множество ребер графа, причем каждое
ребро – это неупорядоченная пара
различных вершин.
– множество ребер графа, причем каждое
ребро – это неупорядоченная пара
различных вершин.
Способы представления графов:
Текстовый
Графический
Матрицами
Определение.
Матрицей смежностиn-вершинного
графа называется квадратная матрица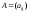 размераn, такая что
размераn, такая что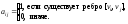
Матрица смежности любого графа обладает следующими свойствами:
она симметрична относительно главной диагонали;
на её главной диагонали стоят нули;
сумма элементов i-й строки (i-го столбца) равнаdeg(vi), т.е. количеству ребер, инцидентных вершинеvi.
В матрице инциденций всегда выполнены следующие условия:
сумма элементов любого её столбца равна двум;
сумма элементов i-й строки равнаdeg(vi).
Определение.
Матрицей инциденцийn-вершинного
графа сmребрами называется
матрица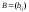 размераn
размераn т,
такая что
т,
такая что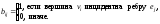
|
Для графа на рис.1 с указанной там нумерацией вершин матрица смежности имеет вид
Если
его ребра пронумеровать
|
Рис.1 |
Утверждение. Для любого графаG= (V,E) сnвершинами иmребрами справедливо равенство т.е. сумма степеней всех вершин графа равна удвоенному количеству ребер.
Теорема о рукопожатиях – в любом графе число вершин нечетной степени четно (если кто-то с кем-то обменялся рукопожатием, число «пожатых рук» четно).









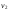

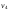
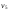
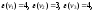
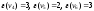 .
. .
.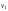
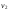
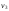



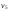
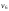

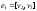 ,
,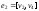 ,
,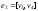 ,
,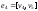 ,
то матрица инциденций этого графа
будет иметь вид
,
то матрица инциденций этого графа
будет иметь вид