
discrete_math
.pdf
Дискретная математика
Оглавление |
|
|
Дискретная математика ....................................................................................................................................... |
1 |
|
Теория графов ....................................................................................................................................................... |
3 |
|
1. Основные понятия теории графов, удаленность вершины, центр, радиус и диаметр графа. .................................................. |
3 |
|
2. Способы задания графов, свойства матриц смежности и инциденций, теорема о рукопожатиях. ......................................... |
3 |
|
3. Основные операции над графами, неравенства для числа вершин, ребер и компонент связности графа. ............................ |
4 |
|
4. Типы графов, дополнительные графы, двудольные графы, критерий двудольности. ............................................................. |
5 |
|
5. Обходы графов: эйлеровы цепи и циклы, необходимые и достаточные условия их существования, алгоритм Флери. ...... |
5 |
|
6. Обходы графов: гамильтоновы цепи и циклы, достаточные условия их существования........................................................ |
5 |
|
7. Деревья, их свойства, кодирование деревьев, остовные деревья. .............................................................................................. |
6 |
|
8. Экстремальные задачи теории графов: минимальное остовное дерево, алгоритмы Прима и Краскала. ............................... |
6 |
|
9. Экстремальные задачи теории графов: задача коммивояжера, «жадный» алгоритм ............................................................... |
7 |
|
10. |
Экстремальные задачи теории графов: задача о кратчайшем пути, алгоритм Дейкстры. ..................................................... |
7 |
11. |
Изоморфизм и гомеоморфизм графов, методы доказательства изоморфности и неизоморфности графов. ....................... |
7 |
12. |
Плоские укладки графов, планарные графы, критерий Понтрягина-Куратовского............................................................... |
8 |
13. |
Необходимые условия планарности, формула Эйлера для планарных графов. ..................................................................... |
8 |
14. |
Правильные вершинные раскраски графов, хроматическое число, неравенства для хроматического числа...................... |
8 |
15. |
Теорема о пяти красках, гипотеза четырех красок, «жадный» алгоритм. ............................................................................... |
9 |
16. |
Хроматический многочлен, его нахождение и свойства........................................................................................................... |
9 |
17. |
Задача о поиске выхода из лабиринта, реберная раскраска графа. ........................................................................................ |
10 |
18. |
Ориентированные графы, источники и стоки, топологическая сортировка, алгоритм Демукрона. ................................... |
10 |
19. |
Составление расписания выполнения комплекса работ в кратчайшие сроки методами теории графов............................ |
10 |
Теория булевой алгебры .................................................................................................................................... |
11 |
|
20. |
Элементарные булевы функции и способы их задания (табличный, векторный, формульный, графический, карта |
|
Карно). ............................................................................................................................................................................................... |
11 |
|
21. |
Существенные и фиктивные переменные булевых функций, основные тождества, эквивалентные преобразования |
|
формул. .............................................................................................................................................................................................. |
12 |
|
22. |
Линейные и нелинейные полиномы Жегалкина, разложение булевых функций в полином Жегалкина методом |
|
неопределенных коэффициентов. ................................................................................................................................................... |
13 |
|
23. |
Линейные и нелинейные полиномы Жегалкина, разложение булевых функций в полином Жегалкина методом |
|
эквивалентных преобразований. ..................................................................................................................................................... |
13 |
|
24. |
Разложение булевых функций в СДНФ и СКНФ. ................................................................................................................... |
14 |
25. |
Минимизация ДНФ и КНФ методом эквивалентных преобразований. ................................................................................ |
14 |
26. |
Минимизация ДНФ и КНФ с помощью карт Карно................................................................................................................ |
15 |
27. |
Замкнутые классы булевых функций Т0, Т1, L, лемма о нелинейной функции. ................................................................... |
15 |
28. |
Замкнутые классы булевых функций S и М, леммы о несамодвойственной и немонотонной функции. .......................... |
16 |
29. |
Полная система функций, теорема о двух системах булевых функций. ............................................................................... |
16 |
30. |
Теорема Поста о полноте системы булевых функций, алгоритм проверки системы на полноту, базис. ........................... |
17 |
31. |
Схемы из функциональных элементов, правила построения и функционирования, метод синтеза СФЭ, основанный на |
|
СДНФ и СКНФ. ................................................................................................................................................................................ |
17 |
|
32. |
Метод синтеза СФЭ, основанный на компактной реализации всех конъюнкций с помощью универсального |
|
многополюсника, сложность получаемых схем. ........................................................................................................................... |
17 |
|
Элементы комбинаторики ................................................................................................................................. |
18 |
|
33. |
Основные комбинаторные операции, сочетания и размещения (с возвращением и без возвращения элементов). .......... |
18 |
34. |
Комбинаторные принципы сложения, умножения, дополнения, включения-исключения. ................................................ |
19 |
|
|
1 |
35. |
Биномиальные коэффициенты, их свойства, бином Ньютона. .............................................................................................. |
19 |
36. |
Треугольник Паскаля, полиномиальная формула. .................................................................................................................. |
19 |
Теория кодирования ........................................................................................................................................... |
20 |
|
37. |
Алфавитное кодирование: необходимое и достаточные условия однозначности декодирования. .................................... |
20 |
38. |
Алфавитное кодирование: теорема Маркова, алгоритм Маркова.......................................................................................... |
21 |
39. |
Коды с минимальной избыточностью (коды Хаффмана), метод построения. ...................................................................... |
22 |
40. |
Линейные коды, порождающая матрица, двойственный код................................................................................................. |
23 |
41. |
Самокорректирующиеся коды (коды Хэмминга), метод построения. ................................................................................... |
23 |
Теория автоматов................................................................................................................................................ |
24 |
|
42. |
Определение, схема и функционирование абстрактного автомата, способы задания автоматов. ...................................... |
24 |
43. |
Типы конечных автоматов, автоматы Мили и Мура, автоматы-генераторы. ....................................................................... |
26 |
44. |
Слова и языки, операции над ними, их свойства. .................................................................................................................... |
26 |
45. |
Регулярные выражения и регулярные языки, теорема Клини. ............................................................................................... |
27 |
46. |
Задача анализа автоматов-распознавателей. ............................................................................................................................ |
28 |
47. |
Задача синтеза автоматов-распознавателей. ............................................................................................................................ |
29 |
48. |
Эквивалентные состояния автомата-распознавателя, эквивалентные автоматы-распознаватели, минимизация |
|
автоматов-распознавателей, алгоритм Мили. ................................................................................................................................ |
31 |
|
49. |
Эквивалентные состояния автомата-преобразователя, эквивалентные автоматыпреобразователи, минимизация |
|
автоматовпреобразователей, алгоритм Мили. ............................................................................................................................. |
33 |
|
50. |
Детерминированные и недетерминированные функции, примеры, способы задания. ........................................................ |
33 |
51. |
Ограниченно-детерминированные (автоматные) функции, способы их задания................................................................. |
34 |
52. |
Логические автоматы, способы их задания, синтез двоичного сумматора. .......................................................................... |
35 |
53. |
Операции над логическими автоматами: суперпозиция и введение обратной связи........................................................... |
36 |
2
Теория графов
1. Основные понятия теории графов, удаленность вершины, центр, радиус и диаметр графа.
Графом G называется пара (V, E), где V v1,...,vn – непустое множество вершин графа, а |
E {e1, e2 ,...,em} |
– множество |
|||||
ребер графа, причем каждое ребро – это неупорядоченная пара различных вершин. |
|
|
|
|
|
|
|
Пусть ребро е соединяет вершины u и v. В этом случае пишут e = [u,v] и |
|
|
|
v |
|
||
говорят, что |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
u и v являются концами ребра е; |
v2 |
v3 |
|
||||
|
вершины u и v смежны; |
|
|||||
|
|
|
|
|
|
||
вершины u и v инцидентны ребру е, ребро е инцидентно вершинам u |
|
|
|
|
|
|
|
|
и v. |
|
|
|
v4 |
|
|
Определение. Степенью вершины называется количество инцидентных ей |
|
|
|
|
|||
|
|
|
|
||||
|
|
|
|
|
|
||
ребер. |
|
|
|
|
|
|
|
Определение. Вершина называется изолированной, если она не инцидентна |
|
|
|
v |
|
||
|
|
|
|
|
|
||
ни одному ребру; вершина называется концевой, если ей инцидентно только |
|
|
|
5 |
|
|
|
одно ребро. |
Рис.1 |
|
Утверждение. Если в графе количество вершин n ≥ 2, то в нем найдутся хотя бы две вершины с одинаковой степенью. Утверждение. Для любого графа G = (V,E) с n вершинами и m ребрами справедливо равенство т.е. сумма степеней всех вершин графа равна удвоенному количеству ребер.
Определение. Последовательность ребер [v1, v2 ], [v2 , v3 ],..., [vk 1, vk ], [vk , vk 1] , в которой все ребра различны, называется
цепью длины k, соединяющей вершины |
v1 |
и |
v |
Определение. Расстоянием между вершинами
k 1 |
. При этом вершины |
u и v называется число
v1
и vk (u, v)
1 |
называются концами цепи. |
, равное длине кратчайшей цепи, соединяющей
вершины u и v. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение. Эксцентриситетом вершины u называется число |
(u) , |
равное максимальному расстоянию от вершины u до |
|||||||||||
остальных вершин графа, т.е. |
(u) max (u, v) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v V |
|
|
|
|
|
|
|
|
|
|
|
Определение. Радиусом графа G |
называется |
число |
r(G), |
равное |
минимальному |
эксцентриситету |
его |
вершин, |
т.е. |
||||
r(G) min (v) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
v V |
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение. Диаметром графа G |
называется |
число |
d(G), |
равное |
максимальному |
эксцентриситету |
его |
вершин, |
т.е. |
||||
d (G) max (v) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
v V |
|
|
|
|
|
|
|
|
|
|
|
|
|
Известно, что для любого графа G выполняется соотношение r(G) d(G) 2 r(G) . |
|
|
|
|
|
|
|
||||||
Определение. Центром графа G называется множество его вершин, имеющих минимальный эксцентриситет. |
|
|
|||||||||||
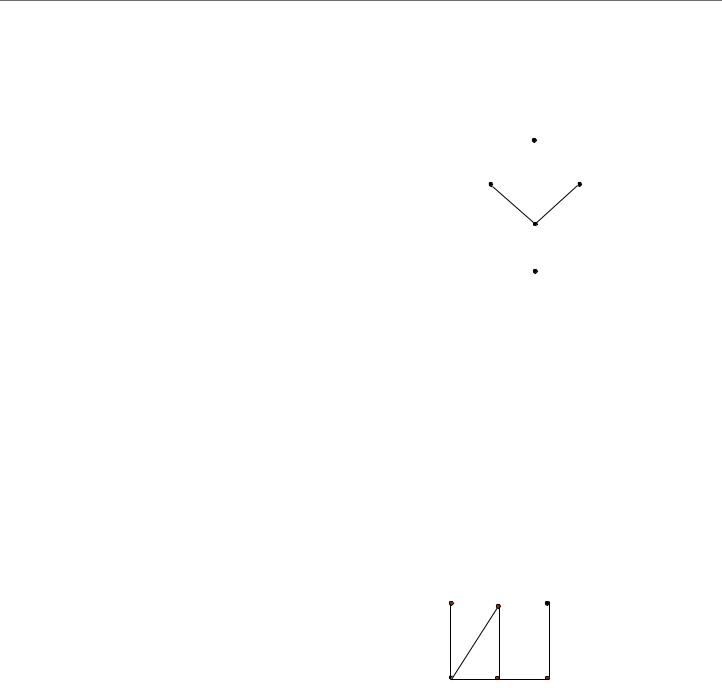
Пример 2. Рассмотрим |
граф |
G, изображенный |
на |
рис.2. |
v |
v |
2 |
v |
3 |
|
|
|
|
Эксцентриситеты его вершин: |
|
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
(v ) 4, (v ) 3, (v ) 4, |
|
|
|
|
|
|
|
|
|
|
|
||
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
(v4 ) 3, (v5 ) 2, (v6 ) 3 . |
|
|
|
|
|
|
|
|
|
|
|
||
Следовательно, |
его радиус и диаметр r(G) = 2, |
d(G) = 4, |
а центр – |
|
|
|
|
|
||
вершина v |
5 |
. |
|
|
v |
4 |
v |
5 |
v |
6 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||
Рис.2
2. Способы задания графов, свойства матриц смежности и инциденций, теорема о рукопожатиях.
Графом G называется пара (V, E), где V v1,...,vn – непустое множество вершин графа, а E {e1, e2 ,...,em} – множество
ребер графа, причем каждое ребро – это неупорядоченная пара различных вершин. Способы представления графов:
Текстовый
Графический
Матрицами
Определение. |
Матрицей смежности n-вершинного графа называется квадратная матрица A (aij ) размера n, такая что |
||
|
i |
j |
|
1, если существует ребро [v , v |
|
], |
|
aij |
|
|
|
0, иначе. |
|
|
|
Матрица смежности любого графа обладает следующими свойствами:
она симметрична относительно главной диагонали;
3

на её главной диагонали стоят нули;
сумма элементов i-й строки (i-го столбца) равна deg(vi), т.е. количеству ребер, инцидентных вершине vi.
Вматрице инциденций всегда выполнены следующие условия:
сумма элементов любого её столбца равна двум;
сумма элементов i-й строки равна deg(vi).
Определение. Матрицей инциденций n-вершинного графа с m ребрами называется матрица
B (b |
) |
ij |
|
размера n т, такая что
b |
|
1, если вершина |
v |
инцидентна |
ребру |
е |
|
, |
|
i |
|
|
|
j |
|
||
ij |
|
|
|
|
|
|
|
|
|
|
0, иначе. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для графа на рис.1 с указанной там нумерацией вершин матрица смежности имеет вид
 v1
v1
0 |
0 |
0 |
0 |
0 |
||
|
0 |
0 |
1 |
1 |
0 |
|
A |
0 |
1 |
0 |
1 |
0 |
|
|
0 |
1 |
1 |
0 |
1 |
|
|
0 |
0 |
0 |
1 |
0 |
|
|
|
|||||
Если его |
ребра пронумеровать |
|
e1 [v2 |
, v3 ] , |
e2 [v2 , v4 ] , |
e3 |
||
e4 [v4 , v5 |
] , то матрица инциденций этого графа будет иметь вид |
|||||||
|
0 |
0 |
0 |
0 |
|
|
||
|
|
1 |
1 |
0 |
0 |
|
|
|
|
B |
1 |
0 |
1 |
0 |
|
|
|
|
|
0 |
1 |
1 |
1 |
|
|
|
|
|
0 |
0 |
0 |
1 |
|
|
|
|
|
|
|
|
||||
[v |
, v |
4 |
] |
3 |
|
|
,
v |
2 |
v |
3 |
|
|
||
|
|
v |
|
|
|
4 |
|
|
|
v |
|
|
|
5 |
|
Рис.1
Утверждение. Для любого графа G = (V,E) с n вершинами и m ребрами справедливо равенство т.е. сумма степеней всех вершин графа равна удвоенному количеству ребер.
Теорема о рукопожатиях – в любом графе число вершин нечетной степени четно (если кто-то с кем-то обменялся рукопожатием, число «пожатых рук» четно).
3. Основные операции над графами, неравенства для числа вершин, ребер и компонент связности графа.
Графом G называется пара (V, E), где V v1,...,vn – непустое множество вершин графа, а
E {e |
, e |
,...,e |
} |
1 |
2 |
m |
|
– множество
ребер графа, причем каждое ребро – это неупорядоченная пара различных вершин.
Утверждение. Если в графе количество вершин n ≥ 2, то в нем найдутся хотя бы две вершины с одинаковой степенью. Утверждение. Для любого графа G = (V,E) с n вершинами и m ребрами справедливо равенство т.е. сумма степеней всех вершин графа равна удвоенному количеству ребер.
Кграфам или отдельным его элементам могут применяться следующие операции:
добавление ребра, соединяющего две несмежные вершины;
удаление ребра (концы ребра сохраняются);
добавление вершины;
удаление вершины (вместе с инцидентными ей ребрами);
отождествление двух несмежных вершин (все ребра, инцидентные отождествляемым вершинам, сохраняются и становятся инцидентными полученной вершине; если при этом возникают кратные ребра, они заменяются одним ребром);
подразбиение ребра [u,v] (сначала добавляются новая вершина w и новые ребра [u,w], [w,v], затем удаляется ребро
[u,v]);
стягивание ребра [u,v] (сначала удаляется ребро [u,v], а затем вершины u и v отождествляются);
объединение графов G1 вершины и ребра графов
и
G1
G2
и
(в результате получается граф
G2 ).
G1 U
G2
, вершинами и ребрами которого являются
Определение. Граф называется связным, если в нем любые две вершины соединены цепью.
Определение. Говорят, что граф состоит из k компонент связности, если его можно представить как объединение k связных графов, не имеющих общих вершин.
Определение. Мостом в графе называется ребро, при удалении которого увеличивается количество компонент связности этого графа.
Утверждение 1. Количество ребер m в любом связном n-вершинном графе удовлетворяет неравенствам |
n 1 m |
1 |
n(n 1) |
|
2 |
||||
|
|
|
||
. |
|
|
|
Утверждение 2. Если n-вершинный граф состоит из k компонент связности, то количество его ребер m удовлетворяет неравенствам n k m 12 (n k)(n k 1) .
4

4. Типы графов, дополнительные графы, двудольные графы, критерий двудольности.
Графом G называется пара (V, E), где
V
v |
,...,v |
1 |
n |
– непустое множество вершин графа, а
E {e |
, e |
,...,e |
} |
1 |
2 |
m |
|
– множество
ребер графа, причем каждое ребро – это неупорядоченная пара различных вершин.
Определение. Полный n-вершинный граф (клика) – это граф, в котором любые две вершины соединены ребром (обозначается Kn );
Определение. Нулевой n-вершинный граф – это граф без ребер (обозначается On );
Определение. Граф называется связным, если в нем любые две вершины соединены цепью.
Определение. Двудольный граф – это граф, множество вершин которого можно так разбить на два непересекающихся подмножества (доли) V1 и V2 , что никакие две вершины из одной доли не смежны;
Утверждение. Критерий двудольности графа - необходимо и достаточно, чтобы в этом графе все циклы имели четную длину.
Определение. Полный двудольный граф – это двудольный граф, в котором каждая вершина из доли V1 |
смежна каждой |
вершине из доли V2 (обозначается Kn,m , где n, m – количество вершин в V1 и V2 ).
Определение. Дополнительным графом к n-вершинному графу G называется граф
G
с тем же множеством вершин, не
имеющий с графом
G
общих ребер, и такой, что
G
U G
Kn
.
5. Обходы графов: эйлеровы цепи и циклы, необходимые и достаточные условия их существования, алгоритм Флери.
Графом G называется пара (V, E), где
V
v |
,...,v |
1 |
n |
– непустое множество вершин графа, а
E {e |
, e |
,...,e |
} |
1 |
2 |
m |
|
– множество
ребер графа, причем каждое ребро – это неупорядоченная пара различных вершин.
Определение. Эйлерова цепь – цепь, подразумевающая обход всех вершин через единичное прохождение каждого ребра, но не подразумевающая возврат в изначальную точку.
Определение. Эйлеров цикл – цикл, при котором происходит обход всех вершин через единичное прохождение каждого ребра.
Утверждение. Критерий существования эйлерова цикла - только тогда, когда в графе все вершины имеют четную степень; связность.
Утверждение. Критерии существования эйлеровой цепи - существует тогда и только тогда, когда в графе ровно две вершины имеют четную степень; связность.
Граф, в котором существует эйлеров цикл, называется эйлеровым графом. Существует алгоритм Флери для построения эйлерового цикла в эйлеровом графе. Этот алгоритм нумерует ребра графа в порядке их прохождения, а сам порядок определяется следующей схемой:
Из произвольной начальной вершины по любому инцидентному ей ребру переходим в следующую вершину, нумеруем это ребро цифрой 1 и удаляем его.
Если очередной вершине инцидентно только одно ребро, то переходим по нему в следующую вершину, нумеруем это ребро очередным числом и удаляем его. Если же очередной вершине инцидентны несколько ребер, то среди них
обязательно найдется ребро, которое не является мостом в оставшемся графе. По этому ребру переходим в следующую вершину, нумеруем это ребро очередным числом и удаляем его. Этот этап повторяется до тех пор, пока не удалим все ребра графа.
Алгоритм заканчивает работу за конечное число шагов, равное количеству ребер в исходном графе. При этом номера ребер указывают, в каком порядке следуют ребра в эйлеровом цикле.
6. Обходы графов: гамильтоновы цепи и циклы, достаточные условия их существования.
Графом G называется пара (V, E), где V v1,...,vn – непустое множество вершин графа, а E {e1, e2 ,...,em} – множество
ребер графа, причем каждое ребро – это неупорядоченная пара различных вершин.
Определение. Гамильтонова цепь – цепь, соединяющая разные вершины графа и проходящая через каждую вершину графа ровно по одному разу (связность графа – необходимое условие наличия).
Определение. Гамильтонов цикл - цикл, соединяющий разные вершины графа и проходящий через каждую вершину графа ровно по одному разу (связность графа – необходимое условие наличия).
Утверждение. Достаточное условие существования гамильтонова цикла - если в связном n-вершинном графе, где n ≥ 3, степень каждой вершины deg(v) ≥ n/2, то в этом графе имеется гамильтонов цикл.
Утверждение. Если в связном n-вершинном графе, где n ≥ 3, степень каждой вершины deg(v) ≥ n/2, то в этом графе имеется гамильтонов цикл.
Определение. Граф, в котором имеется гамильтонов цикл, называется гамильтоновым.
5
7. Деревья, их свойства, кодирование деревьев, остовные деревья.
Определение. Связный граф без циклов называется деревом. Графом G называется пара (V, E), где V v1,...,vn – непустое множество вершин графа, а E {e1, e2 ,...,em} – множество ребер графа, причем каждое ребро – это неупорядоченная пара
различных вершин.
Свойство 1. Если две произвольные несмежные вершины дерева соединить ребром, то в нем возникнет простой цикл. Свойство 2. В дереве любое ребро является мостом Свойство 3. В дереве количество ребер на единицу меньше числа вершин.
Определение. Ребро дерева называется концевым ребром, если оно инцидентно концевой вершине (т.е. вершине степени 1). Свойство 4. В любом n-вершинном дереве при n 2 существует не менее двух концевых вершин и не менее одного концевого ребра.
Свойство 5. В любом n-вершинном дереве при n 3 есть хотя бы одна неконцевая вершина.
Определение. Дерево с выделенной вершиной называется корневым деревом, а выделенная вершина – корнем дерева.
Построение кода основано на обходе дерева «в глубину», при котором |
v |
v |
2 |
v |
3 |
|
|
|
каждое ребро проходится дважды: первый раз – в направлении от корня, |
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
второй раз – к корню. Каждое ребро кодируется двумя символами – 0 и 1. |
|
|
|
v4 |
|
|
|
|
При этом ноль означает движение вдоль данного ребра от корня, а единица |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
– к корню. В получающемся коде ноль и единица, соответствующие одному |
|
|
|
|
|
|
|
|
и тому же ребру, не обязательно стоят рядом. |
|
|
|
|
v5 |
|
|
v6 |
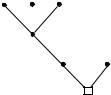
Пример 1. Корнем дерева на рисунке является вершина v7 . При его обходе |
|
|
|
|
|
|
v |
|
«в глубину» из корня получаем последовательность вершин: v7, v5, v4, v1, v4, |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
v2, v4, v3, v4, v5, v7, v6, v7. Такой обход порождает код (000101011101). |
|
|
|
|
|
|
рисунок |
|
Заметим, что иному обходу этого же дерева v7, v6, v7, v5, v4, v1, v4, v2, v4, v3, |
|
|
|
|
|
|
|
|
v4, v5, v7 соответствует другой код (010001010111).
Определение. Остовным деревом связного графа называется дерево, получающееся из этого графа путем удаления некоторых ребер (все вершины графа при этом сохраняются).
Определение. Минимальное остовное дерево - остовное дерево минимально возможной длины. Для его построения существует алгоритм Краскала. Идея этого алгоритма состоит в том, что искомое остовное дерево «вырастает» из леса, отдельные деревья которого постепенно объединяются и на последнем шаге алгоритма объединяются в одну компоненту связности – остовное дерево. Схема алгоритма такова:
Из исходного графа убрать кратчайшее ребро и перенести его в нулевой граф с тем же числом вершин. Получим лес, состоящий из одного ребра и множества изолированных вершин.
Из оставшихся ребер исходного графа убрать кратчайшее, которое после добавления его к полученному лесу не образует там циклов. Этот этап повторяется до тех пор, пока лес не превратится в остовное дерево исходного графа.
8.Экстремальные задачи теории графов: минимальное остовное дерево, алгоритмы Прима и Краскала.
Определение. Связный граф без циклов называется деревом. Графом G называется пара (V, E), где V v1,...,vn – непустое множество вершин графа, а E {e1, e2 ,...,em} – множество ребер графа, причем каждое ребро – это неупорядоченная пара
различных вершин.
Определение. Если задача состоит в том, чтобы найти экстремум (максимум или минимум) определенной функции от этих значений, то её принято называть экстремальной задачей.
Определение. Остовным деревом связного графа называется дерево, получающееся из этого графа путем удаления некоторых ребер (все вершины графа при этом сохраняются).
Определение. Минимальное остовное дерево - остовное дерево минимально возможной длины.
Алгоритм Прима. В графе G=(V, E) рассмотрим U - некоторое подмножество V, такое что U и V-U не пусты. Пусть (u, v) - ребро наименьшей стоимости, одна вершина которого - u принадлежит U, а другая - v принадлежит V-U. Тогда существует некоторое минимальное остовное дерево, содержащее ребро (u, v). Начинаем с пустого U=0. Добавляем к U вершины, каждый раз находя ребро наименьшей стоимости между U и V-U.
Положить в U любую вершину (изначально U – пусто).
До тех пор, пока ( V-U не пусто ): выбираем ребро (u, v) наименьшей стоимости, u из U, v из V-U; добавляем v к U
(и убираем из V-U)
Алгоритм Краскала. Идея алгоритма Краскала состоит в том, что искомое остовное дерево «вырастает» из леса, отдельные деревья которого постепенно объединяются и на последнем шаге алгоритма объединяются в одну компоненту связности – остовное дерево. Схема алгоритма такова:
Из исходного графа убрать кратчайшее ребро и перенести его в нулевой граф с тем же числом вершин. Получим лес, состоящий из одного ребра и множества изолированных вершин.
Из оставшихся ребер исходного графа убрать кратчайшее, которое после добавления его к полученному лесу не образует там циклов. Этот этап повторяется до тех пор, пока лес не превратится в остовное дерево исходного графа.
6
9. Экстремальные задачи теории графов: алгоритм
Определение. Графом G называется пара (V, E), где V v1,...,vn
задача коммивояжера, «жадный»
– непустое множество вершин графа, а |
E {e1, e2 ,...,em} |
– множество ребер графа, причем каждое ребро – это неупорядоченная пара различных вершин.
Определение. Если задача состоит в том, чтобы найти экстремум (максимум или минимум) определенной функции от этих значений, то её принято называть экстремальной задачей.
Определение. Гамильтонов цикл - цикл, соединяющий разные вершины графа и проходящий через каждую вершину графа ровно по одному разу (связность графа – необходимое условие наличия).
Задача коммивояжера связана с поиском гамильтонова цикла в графе. Для ее решения разработаны приближенные алгоритмы, которые при одних входных данных дают правильное решение, а при других – «приближенное» с заранее известной погрешностью. Иногда этого свойства алгоритма бывает вполне достаточно для его практического применения. Рассмотрим один из них, относящийся к классу так называемых «жадных» алгоритмов. Он состоит в следующем:
пометить кратчайшее ребро графа (оно обязательно войдет в гамильтонов цикл, который в итоге будет построен);
среди непомеченных ребер найти кратчайшее, причем такое, которое вместе с уже помеченными ребрами не образует вершин степени три и циклов, состоящих менее чем из n вершин; пометить найденное ребро (этот шаг повторяется до тех пор, пока в дополнительном графе не образуется гамильтонов цикл).
10.Экстремальные задачи теории графов: задача о кратчайшем пути, алгоритм Дейкстры.
Определение. Графом G называется пара (V, E), где
V
v |
,...,v |
1 |
n |
– непустое множество вершин графа, а
E {e |
, e |
,...,e |
} |
1 |
2 |
m |
|
– множество ребер графа, причем каждое ребро – это неупорядоченная пара различных вершин.
Определение. Если задача состоит в том, чтобы найти экстремум (максимум или минимум) определенной функции от этих значений, то её принято называть экстремальной задачей.
Задача о кратчайшем пути - поиск кратчайшего пути между двумя вершинами в предположении, что каждое ребро графа имеет определенную длину. Например, пусть имеется сеть дорог, соединяющих несколько населенных пунктов. Часто возникает задача найти такой путь для перевозки груза из пункта А в пункт В через другие промежуточные пункты, чтобы суммарная длина дорог, составляющих этот путь, была минимальна. Иногда требуется, чтобы такой путь обеспечивал минимальное время или минимальные затраты на перевозку груза из А в В. Всё это разные варианты задачи о кратчайшем пути. Схема алгоритма Дейкстры для решения задачи о кратчайшем пути такова:
1.найти вершину и1, ближайшую к вершине и0 (выбирается кратчайшее ребро, инцидентное вершине и0);
2.пусть уже найдены k самых близких к и0 вершин и1, и2,…, иk и известны величины d(и1), d(и2),…, d(иk) – их удаленности от вершины и0 (причем d(и1) ≤ d(и2) ≤ … ≤ d(иk)); тогда для каждой вершины и из множества V \{и0, и1, и2,…, иk} вычислить параметр D(и), задаваемый равенством D(и) = min{d(иi) + l (ui, u)},
3.где минимум берется по i = 0, 1, 2,…, k, а l (ui, u) – длина ребра [ui, u];
4.следующая вершина иk+1 – ближайшая к и0 среди всех вершин из множества V \{и0, и1, и2,…, иk} – находится из
условия D(иk+1) = min{D(и)}, где минимум ищется по всем вершинам и из множества V \{и0, и1, и2,…, иk};
5.положить d(иk+1) = D(иk+1).
Шаги 2 – 4 повторяются в цикле по k = 1, 2, 3,…, n – 1.
11. Изоморфизм и гомеоморфизм графов, методы доказательства изоморфности и неизоморфности графов.
Определение. Графом G называется пара (V, E), где V v1,...,vn – непустое множество вершин графа, а
– множество ребер графа, причем каждое ребро – это неупорядоченная пара различных вершин.
E {e |
, e |
,...,e |
} |
1 |
2 |
m |
|
Всякий граф можно изобразить на плоскости в виде точек и непрерывных линий, соединяющих эти точки. При этом один и
тот же граф может иметь бесконечно много различных изображений (укладок графа на плоскости).
Определение. Говорят, что взаимно однозначное соответствие между множествами вершин двух графов сохраняет смежность вершин, если любой паре смежных вершин первого графа соответствует пара смежных вершин второго.
|
|
|
Определение. Два графа G (V , E) и G |
(V , E ) |
|
соответствие между множествами вершин V и V
называются изоморфными, если существует взаимно однозначное , которое сохраняет смежность вершин.
Чтобы доказать, что два графа не изоморфны, надо найти какую-либо характеристику этих графов, по которой они различаются. Для графов сложной структуры с большим количеством вершин и ребер подобрать такую характеристику иногда бывает очень трудно. Поэтому проблема изоморфизма считается одной из самых сложных в теории графов.
Также установить изоморфизм двух графов можно и с помощью их матриц смежности. Для этого надо одну матрицу преобразовать в другую одновременной перестановкой некоторых её строк и столбцов. Однако если заранее не известно, изоморфны ли данные графы, такой способ проверки изоморфизма, так же как и перебор всех возможных вариантов взаимно однозначного соответствия между вершинами графов, требует большого объема вычислений.
7
Определение. Два графа называются гомеоморфными, если их можно получить из одного графа с помощью однократного или многократного применения операции подразбиения ребра.
12. Плоские укладки графов, планарные графы, критерий ПонтрягинаКуратовского.
Определение. Графом G называется пара (V, E), где V v1,...,vn – непустое множество вершин графа, а |
E {e1, e2 ,...,em} |
– множество ребер графа, причем каждое ребро – это неупорядоченная пара различных вершин. |
|
Всякий граф можно изобразить на плоскости в виде точек и непрерывных линий, соединяющих эти точки. При этом один и
тот же граф может иметь бесконечно много различных изображений (укладок графа на плоскости).
Определение. Изображение графа на плоскости без внутренних точек пересечения ребер называется плоской укладкой графа.
Определение. Граф называется планарным, если существует его плоская укладка.
Утверждение 1 (необходимое условие планарности). Для любого связного планарного графа с n вершинами и m ребрами, где n ≥ 3, выполняется неравенство m 3n 6 .
Утверждение 2 (необходимое условие планарности). В любом планарном графе есть вершина, степень которой не
превосходит пяти. |
|
|
|
|
|
|
|
|
|
|
|
|
Определение. |
Два графа называются гомеоморфными, если |
u |
|
u |
2 |
u |
3 |
|
|
|
||
их можно получить из одного графа с помощью однократного |
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
или многократного применения операции подразбиения |
|
|
|
|
|
|
|
|
|
|||
ребра. |
|
|
|
|
|
|
|
|
|
|
|
|
Критерий |
планарности |
(критерий |
Понрягина- |
|
|
|
|
|
|
|
|
|
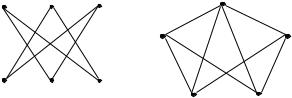
Куратовского). Граф планарен тогда и только тогда, когда в |
|
|
|
|
|
|
|
|
|
|||
нем нет подграфов, гомеоморфных графу К5 или К3,3. |
v |
|
v |
2 |
v |
3 |
|
|
|
|||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
|
|
|
|
|
|
||
|
|
|
|
|
K3,3 |
|
|
|
K5 |
|
||
13. Необходимые условия планарности, формула Эйлера для планарных графов.
Определение. Графом G называется пара (V, E), где V v1,...,vn – непустое множество вершин графа, а
– множество ребер графа, причем каждое ребро – это неупорядоченная пара различных вершин.
E {e |
, e |
,...,e |
} |
1 |
2 |
m |
|
Всякий граф можно изобразить на плоскости в виде точек и непрерывных линий, соединяющих эти точки. При этом один и
тот же граф может иметь бесконечно много различных изображений (укладок графа на плоскости).
Определение. Изображение графа на плоскости без внутренних точек пересечения ребер называется плоской укладкой графа.
Определение. Граф называется планарным, если существует его плоская укладка.
Утверждение 1 (необходимое условие планарности). Для любого связного планарного графа с n вершинами и m ребрами, где n ≥ 3, выполняется неравенство m 3n 6 .
Утверждение 2 (необходимое условие планарности). В любом планарном графе есть вершина, степень которой не превосходит пяти.
Определение. Говорят, что граф состоит из k компонент связности, если его можно представить как объединение k связных графов, не имеющих общих вершин.
Формула Эйлера. Для всякого планарного графа справедлива формула Эйлера: n g m k 1, где n – количество вершин,
g – граней, m – ребер, k – компонент связности в исходном графе. Под гранями здесь понимаются связные области, на которые распадается плоскость, если провести «разрезы» по всем ребрам плоской укладки графа. Для связного планарного графа формулу Эйлера можно записать иначе: n g m 2 .
14. Правильные вершинные раскраски графов, хроматическое число, неравенства для хроматического числа.
Определение. Графом G называется пара (V, E), где V v1,...,vn – непустое множество вершин графа, а E {e1, e2 ,...,em}
– множество ребер графа, причем каждое ребро – это неупорядоченная пара различных вершин.
Определение. Говорят, что вершины графа G правильно раскрашены с помощью цветов {c1, c2,…, cr}, если каждой вершине поставлен в соответствие некоторый цвет, причем любым двум смежным вершинам соответствуют разные цвета.
Утверждение 1. Для правильной раскраски вершин любого двудольного графа достаточно двух цветов.
8
Определение. Хроматическим числом графа называется минимальное число красок, достаточное для правильной раскраски его вершин.
Хроматическое число графа G далее будем обозначать через χ(G). Выполняются следующие свойства хроматического числа:
1) |
(Kn ) n ; |
|
|
2) |
если G – двудольный граф, то (G) 2 ; |
|
|
3) |
если Т – дерево, то (T ) 2 |
(так как всякое дерево – двудольный граф); |
|
4) |
если G – планарный граф, то |
(G) 4 . |
|
Утверждение 2. Для любого графа G справедлива верхняя оценка |
(G) d 1, где d = max deg(v). |
||
Определение. Хроматическим многочленом графа G называется многочлен P(G,x), который при каждом целом неотрицательном значении х равен количеству различных способов правильной раскраски вершин графа G с использованием не более х фиксированных цветов.
15. Теорема о пяти красках, гипотеза четырех красок, «жадный» алгоритм.
Определение. Графом G называется пара (V, E), где V v1,...,vn – непустое множество вершин графа, а |
E {e1, e2 ,...,em} |
– множество ребер графа, причем каждое ребро – это неупорядоченная пара различных вершин.
Определение. Говорят, что вершины графа G правильно раскрашены с помощью цветов {c1, c2,…, cr}, если каждой вершине поставлен в соответствие некоторый цвет, причем любым двум смежным вершинам соответствуют разные цвета.
Теорема о пяти красках. Для правильной раскраски вершин любого планарного графа достаточно пяти цветов.
Гипотеза четырех красок. Теорема о пяти красках была доказана в 1890 г. Но ещё раньше, в 1879 г., было высказано предположение о том, что для правильной раскраски вершин планарного графа достаточно четырех красок (так называемая «гипотеза четырех красок»). Долгое время оно так и оставалось гипотезой, и лишь в 1976 г., было получено его доказательство. В настоящее время не все математики считают это доказательство строгим, поскольку оно содержит перебор большого количества графов, который был осуществлен авторами доказательства с помощью компьютера. Снизить количество цветов в «гипотезе четырех красок» до трех цветов нельзя, так как существуют планарные графы, например К4, для правильной раскраски вершин которых уже недостаточно трёх цветов.
«Жадный» алгоритм. Все известные точные алгоритмы поиска минимального числа красок, достаточного для правильной раскраски его вершин, являются переборными, поэтому их сложность быстро возрастает одновременно с ростом числа вершин в графе. Однако есть «жадные» алгоритмы, которые достаточно эффективны, но иногда «завышают» ответ. Пример «жадного» алгоритма:
Нумеруем вершины графа числами 1, 2, 3… n.
В цикле просматриваем вершины в порядке возрастания их номеров, начиная с первой. Если очередная вершина не покрашена, то красим ее в текущий цвет. Если после этого остались непокрашенные вершины, то берем новый цвет и снова проходим по вершинам, крася их.
16.Хроматический многочлен, его нахождение и свойства.
Определение. Графом G называется пара (V, E), где V v1,...,vn – непустое множество вершин графа, а |
E {e1, e2 ,...,em} |
– множество ребер графа, причем каждое ребро – это неупорядоченная пара различных вершин.
Определение. Говорят, что вершины графа G правильно раскрашены с помощью цветов {c1, c2,…, cr}, если каждой вершине поставлен в соответствие некоторый цвет, причем любым двум смежным вершинам соответствуют разные цвета.
Определение. Хроматическим числом графа называется минимальное число красок, достаточное для правильной раскраски его вершин.
Определение. Хроматическим многочленом графа G называется многочлен P(G,x), который при каждом целом неотрицательном значении х равен количеству различных способов правильной раскраски вершин графа G с использованием не более х фиксированных цветов.
Хроматический многочлен легко получить для нулевого и для полного n-вершинного графа. Действительно, P(Оn,x) = хn, поскольку каждую вершину можно покрасить любым из х цветов, независимо от остальных вершин, и все эти раскраски будут правильными. Для полного графа P(Kn,x) = x(x – 1)(x – 2)…(x – n + 1), так как первую вершину можно покрасить любым их х цветов, вторую – любым из х – 1 цветов, третью – любым из х – 2 цветов и т.д.
Утверждение 1. Пусть Tn – произвольное n-вершинное дерево. Тогда P(Tn,x) = x(x – 1)n – 1.
Имеется алгоритм, позволяющий находить хроматический многочлен для графа с произвольной структурой. Он основан на следующем утверждении.
Утверждение 2. Пусть u и v - несмежные вершины графа G, граф G получен путем добавления ребра [u,v] в графе G, а граф G – отождествлением вершин u и v в графе G. Тогда выполняется тождество P(G, x) = P( G , x) + P( G , x).
9

G
G |
|
|
G |
|
|
Пример. Найдем хроматический многочлен графа, изображенного на рисунке. Согласно тождеству (1)
P(G, x) = P( G |
|
, x) + P( G |
|
, x), где G |
|
= K4, а G |
|
|
|
|
|
|
|
|
|
||||
= K3. Таким образом, P(G, x) = |
|
|
|
|
|
||||
x(x 1)( x 2)( x 3) x(x 1)( x 2) x(x 1)( x 2) |
2 |
|
|||||||
|
|||||||||
x |
4 |
5x |
3 |
8x |
2 |
4x . |
|
|
|
Хроматический многочлен графа содержит некоторую дополнительную информацию о самом графе. А именно:
степень хроматического многочлена равна числу вершин;
если степень хроматического многочлена равна n, то коэффициент при хn равен 1, а коэффициент при хn – 1 равен (– m), где m – количество ребер в графе G;
знаки коэффициентов хроматического многочлена чередуются;
хроматическое число графа на единицу больше максимального корня его хроматического многочлена;
хроматический многочлен обращается в нуль при всех целых неотрицательных значениях х, меньших хроматического числа графа.
17.Задача о поиске выхода из лабиринта, реберная раскраска графа.
Определение. Графом G называется пара (V, E), где V v1,...,vn – непустое множество вершин графа, а |
E {e1, e2 ,...,em} |
– множество ребер графа, причем каждое ребро – это неупорядоченная пара различных вершин.
Определение. Говорят, что вершины графа G правильно раскрашены с помощью цветов {c1, c2,…, cr}, если каждой вершине поставлен в соответствие некоторый цвет, причем любым двум смежным вершинам соответствуют разные цвета.
Определение. Реберная раскраска графа называется правильной, если все ребра, инцидентные одной вершине, покрашены в разные цвета.
Задача «поиска выхода из лабиринта».
Изобразим модель лабиринта в виде графа.
Если мы идем по коридору первый раз, то красим его в зеленый цвет.
Когда идем по коридору второй раз, красим его в красный цвет.
По покрашенным в красный цвет коридорам ходить нельзя.
Если из вершины идут несколько коридоров, то выбираем не покрашенный коридор.
Когда идем по коридору первый раз, «разматываем нить».
Когда идем по коридору второй раз, «наматываем нить».
18.Ориентированные графы, источники и стоки, топологическая сортировка, алгоритм Демукрона.
Определение. Графом G называется пара (V, E), где V v1,...,vn – непустое множество вершин графа, а
E {e |
, e |
,...,e |
} |
1 |
2 |
m |
|
– множество ребер графа, причем каждое ребро – это неупорядоченная пара различных вершин.
Определение. Ориентированные графы - графы с ориентированными (имеющими направление) ребрами. У таких графов каждое ребро выходит из его начальной в его конечную вершину и называется дугой. Всякая вершина, в которую не входит ни одна дуга, называется источником, а вершина, из которой нет выходящих дуг – стоком.
Топологической сортировкой ориентированного n-вершинного графа называется процесс, в результате которого каждой вершине приписывается номер из множества {1, 2, …, n} так, чтобы любая дуга была направлена от вершины с меньшим номером к вершине с бóльшим номером. Известно, что топологическая сортировка возможна лишь в том случае, если граф не содержит ориентированных циклов.
Алгоритм Демукрона для топологической сортировки графа. В этом алгоритме циклически повторяется одно и то же действие: в текущем графе находят источники, нумеруют их минимальными числами из текущего множества и затем удаляют их вместе с выходящими из них дугами. В начальный момент текущий граф – это исходный граф, а текущее множество – это множество {1, 2, …, n}. Алгоритм завершает работу, как только все вершины исходного графа окажутся пронумерованными.
19. Составление расписания выполнения комплекса работ в кратчайшие сроки методами теории графов.
Определение. Графом G называется пара (V, E), где V v1,...,vn – непустое множество вершин графа, а E {e1, e2 ,...,em}
– множество ребер графа, причем каждое ребро – это неупорядоченная пара различных вершин.
10
