
discrete_math
.pdf
Необходимое условие однозначности декодирования. Если схема алфавитного кодирования однозначно декодируема, то
для неё выполняется неравенство Макмиллана
r |
l |
|
q |
k |
|
|
|
|
k 1 |
|
|
1
, где r - количество букв в исходном алфавите, q – количество букв
в кодирующем алфавите, а l1, l2,…, lr – длины кодовых слов.
ТЕОРЕМА. Если при некотором q числа l1, l2,…, lr удовлетворяют неравенству Макмиллана, то найдется префиксная (суффиксная) схема алфавитного кодирования с длинами кодовых слов l1, l2,…, lr и кодирующим алфавитом мощности q.
38. Алфавитное кодирование: теорема Маркова, алгоритм Маркова.
Пусть А - исходный алфавит, содержащий буквы
a |
, a |
2 |
,...,a |
r |
1 |
|
|
. В нем записывается исходное сообщение – слово,
составленное из одной или нескольких букв. В кодирующем алфавите B {b1, b2 ,...,bq} записывается закодированное
сообщение. Правила, по которым осуществляется кодирование, могут быть разными. Алфавитное кодирование, как одно из возможных правил, задается схемой Σ вида
где
B |
, B |
2 |
,...,B |
r |
1 |
|
|
a |
B |
, |
|
|
1 |
1 |
|
|
B2 |
|
|
a |
2 |
, |
|
: |
|
|
|
... |
|
||
a |
r |
B |
, |
|
r |
|
|
- слова в кодирующем алфавите. Их называют кодовыми словами. Для того чтобы с помощью такой схемы
закодировать некоторое слово, состоящее из нескольких букв (разрядов), надо каждую букву этого слова закодировать соответствующим ей кодовым словом.
Алфавитное кодирование – кодирование, выполняющееся поразрядно.
Определение. Схема алфавитного кодирования называется однозначно декодируемой, если любое закодированное слово допускает только один способ декодирования.
Определение. Схема алфавитного кодирования называется равномерной, если все её кодовые слова попарно различны, но имеют одинаковую длину.
Теорема Маркова. Для любой схемы алфавитного кодирования Σ существует такое число NΣ, что ~ однозначно декодируемой тогда и только тогда, когда однозначно декодируемы все слова из множества W
схема
( A, N Σ
Σ является
) .
Число N0 можно вычислить через характеристики самой схемы Σ. Для этого нужно рассмотреть все возможные префиксы и
суффиксы кодовых слов |
B |
, B |
,...,B |
схемы Σ. Пусть кодовое слово В |
k |
имеет вид B |
pB |
|
B |
|
...B |
|
s , где р – префикс, s – |
||||
|
|
|
|
|
1 |
2 |
r |
|
k |
k |
k |
2 |
k |
t |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
суффикс, Bk |
, Bk |
2 |
,...,Bk |
t |
- кодовые слова, причем префикс (суффикс) может быть пустым словом Λ, но не должен совпадать |
||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ни с одним из кодовых слов. |
Т - максимальное число кодовых слов, |
которые могут содержаться в разложении другого |
|||||||||||||||
кодового слова. Тогда число NΣ из теоремы Маркова удовлетворяет неравенству
суммарная длина всех кодовых слов |
B1, B2 ,...,Br |
схемы Σ. |
N Σ
1 T
2
1 L r 2
,
где L –
Пример. Требуется оценить сверху число NΣ для схемы Σ с кодовыми словами В1 = ab, В2 = bc, В3 = acb, В4 = abac, В5 = babbc. Проверить, является ли схема однозначно декодируемой. В этой схеме L = 16, r = 5. Для нахождения параметра Т рассмотрим все возможные разложения кодовых слов:
В1 = ab = (a)(b), В2 = bc = (b)(c),
В3 = acb = (a)(cb) = (ac)(b),
В4 = abac = (a)(bac) = [ab](ac) = (aba)(c),
В5 = babbc = (b)[ab][bc] = (ba)(bbc) =(bab)[bc] = (babb)(c),
где для удобства префиксы и суффиксы заключены в круглые скобки, а кодовые слова – в квадратные. В некоторых разложениях префикс или суффикс – пустое слово Λ. Поскольку в разложении кодового слова В5 = (b)[ab][bc] = (b)В1В2 содержится два других кодовых слова, и это максимально возможное количество для данной схемы Σ, то параметр Т = 2.
|
|
|
|
1 |
|
|
||
Следовательно, |
N |
|
|
|
|
2 1 16 5 2 |
19 . |
|
Σ |
|
|||||||
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
||
Алгоритм проверки однозначности декодирования. Опираясь на разложения, построим множество S, включающее все такие префиксы, которые также являются и суффиксами кодовых слов. Также добавим в множество S пустое слово Λ. В данном случае получится множество S = {b, ac, Λ}.
Построим ориентированный граф GΣ с помеченными вершинами и ребрами. Каждая его вершина помечается некоторым элементом множества S. Две вершины соединяются ребром только тогда, когда их метки являются префиксом и суффиксом одного и того же кодового слова. Само ребро помечают частью этого слова, заключенной между префиксом и суффиксом, и ориентируют от вершины-префикса к вершине-суффиксу. В данном случае кодовое слово В5 разложимо в виде В5 = babbc = (b)[ab][bc] = (b)В1В2,
21
т.е. начинается с префикса b и заканчивается пустым суффиксом. Поэтому в графе |
|
GΣ имеется ребро, помеченное словами В1В2 и направленное от вершины b к вершине Λ. |
|
Другое ребро графа GΣ , помеченное словом В1, выходит из вершины Λ в вершину ac, |
|
поскольку кодовое слово В4 = abac = [ab](ac) = В1(ac). |
Λ |
Третье ребро помечено пустым словом Λ и направлено от вершины ac к вершине b, так |
|
как кодовое слово В3 = acb = (ac)(b). Таким образом, получаем граф GΣ, в нем есть |
b |
ориентированный цикл, проходящий через вершину Λ. Данная схема Σ не является |
|
однозначно декодируемой. |
|
Утверждение . Схема алфавитного кодирования Σ является однозначно декодируемой |
|
тогда и только тогда, когда в её графе GΣ нет ориентированного цикла, проходящего через вершину Λ.
ac
В1
В1В2
39. Коды с минимальной избыточностью (коды Хаффмана), метод построения.
Пусть р1, р2,…, рr – частоты (вероятности), с которыми буквы |
|
алфавита |
A {a1, a2 ,...,ar } |
встречаются в исходных |
|||||||||||||||||||||
сообщениях. Частоты неотрицательны и удовлетворяют равенству |
p1 |
p2 |
... pr |
1. |
|
|
|
|
|||||||||||||||||
Определение. Избыточностью схемы алфавитного кодирования Σ с длинами кодовых слов |
l1, |
l2,…, lr при заданных |
|||||||||||||||||||||||
частотах р |
, р |
,…, р |
r |
называется число l ( ) l |
p |
|
l |
p ... l |
p . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
2 |
|
|
1 |
1 |
|
|
2 |
2 |
r r |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Избыточность схемы согласно определению равна l ( ) l1 / r l2 / r ... lr / r (l1 l2 |
... lr ) / r . |
|
|
||||||||||||||||||||||
Пример 1. При заданных частотах р1 = 0.4, р2 = 0.25, р3 = 0.2, р4 = 0.15 сравнить избыточность двух схем Σ1 и Σ2, где |
|
||||||||||||||||||||||||
|
|
|
|
|
|
a |
|
00, |
|
|
|
a |
|
1, |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
: |
a |
2 |
01, |
|
|
: |
a |
2 |
01, |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
1 |
|
a |
3 |
10, |
|
|
a |
3 |
000, |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
a |
11, |
|
|
|
a |
001. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
4 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Заметим, что Σ1 – равномерная схема, а Σ2 – префиксная, поэтому обе эти схемы однозначно декодируемы. В схеме Σ1 |
длины |
||||||||||||||||||||||||
кодовых слов l1 = l2 = l3 = l4 = 2, следовательно, её избыточность равна |
l ( 1) 2 0.4 2 0.25 2 0.2 2 0.15 2 . |
|
|||||||||||||||||||||||
В схеме |
Σ2 |
длины кодовых слов l1 |
|
= |
|
|
|
1, |
l2 = |
2, |
l3 |
|
= |
|
l4 |
= |
3, |
поэтому |
её |
избыточность |
равна |
||||
l ( 2 ) 1 0.4 2 0.25 3 0.2 3 0.15 1.95 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 2. Для набора частот р1 = 0.4, р2 = 0.25, р3 = 0.2, р4 = 0.1, р5 = 0.05 требуется построить суффиксный код Хафмана с исходным алфавитом A {a1, a2 ,...,a5} и кодирующим алфавитом B {0,1} .
Прежде всего, по данному набору частот найдем длины кодовых слов кода Хафмана. Для этого запишем в столбец исходные частоты в порядке их убывания сверху вниз и будем преобразовывать этот столбец, на каждом шаге заменяя две самых маленьких частоты их суммой и располагая в новом столбце полученные частоты в порядке убывания. Процесс преобразования частот завершится, как только мы придем к столбцу с двумя частотами (их сумма равна единице). В таблице показаны столбцы, которые получаются в данном примере. Клетки, выделенные темным цветом, содержат сумму двух самых маленьких
частот из предыдущего столбца.
0.4 |
0.4 |
|
|
0.4 |
|
|
0.6 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
0.25 |
0.25 |
|
|
0.35 |
|
0.4 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
0.2 |
0.2 |
|
|
0.25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.1 |
|
0.15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
0.05 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.6 |
|
|
0.4 |
||||||
|
(0) |
|
|
|||||||
|
|
|
(1) |
|||||||
0.35 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
(00) |
|
|
|
|
|
0.25 |
|
|
||
|
|
|
|
|
|
|
|
|||
0.2 |
0.15 |
|
(01) |
|
|
|||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
(000)(001)
0.1 |
0.05 |
(0010) |
(0011) |
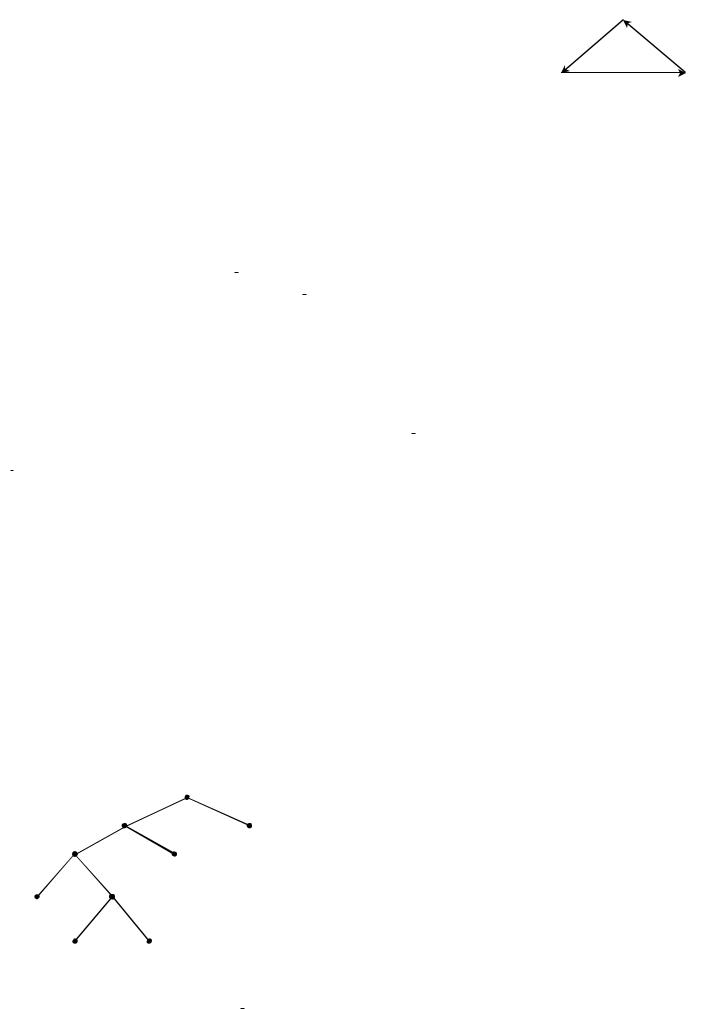
Теперь построим бинарное дерево, корень которого располагается в самом верхнем ярусе. Каждая вершина, кроме корня, помечается числом из таблицы. Построение дерева и расстановка пометок его вершин выполняется рекурсивно. Сначала к единственной вершине – корню дерева – добавляются две смежные с ней вершины, которые помечаются числами из последнего столбца таблицы..
Около каждой концевой вершины дерева указана частота, а в скобках - соответствующее ей кодовое слово кода Хафмана. В итоге получаем
префиксную схему Σп кода Хафмана
a |
1, |
1 |
01, |
a |
: a 000,
п3
a4 0010,a 0011.
52
Однако по условию задачи требовалось построить суффиксную схему кодирования. Она легко получается «зеркальным отражением»
префиксной схемы Σп. Следовательно, искомый суффиксный код
Хафмана |
задается |
схемой |
Σс, |
где |
c :{a1 1, a2 |
10, a3 000, a4 |
0100, a5 1100}. |
|
|
Избыточность построенного кода равна l ( c ) 1 0.4 2 0.25 3 0.2 4 0.1 4 0.05 2.1
22

40. Линейные коды, порождающая матрица, двойственный код.
Определение. Коды с кодирующим алфавитом В = {0,1} называются двоичными кодами.
Определение. Булева функция f (x1,x2,…,xn) называется характеристической функцией двоичного кода, если она обращается в единицу на тех и только тех наборах, которые являются кодовыми словами этого кода.
Утверждение.Пусть |
~ |
~ |
2 |
... n ) |
− два кодовых слова двоичного кода Σ. Через |
~ |
~ |
обозначается |
( 1 2 |
... n ), ( 1 |
( |
, ) |
расстояние Хэмминга между двумя кодовыми словами
~
и |
~ |
|
, которое вычисляется по формуле
~~ n
( , ) i
i1
i 
.
Формула означает, что расстояние Хэмминга между двумя кодовыми словами равно числу позиций, в которых эти слова различаются.
Определение. Кодовым расстоянием двоичного кода называется минимальное расстояние Хэмминга между двумя его кодовыми словами. Кодовое расстояние схемы Σ – это минимальное число позиций, в которых могут отличаться два её
кодовых слова. Геометрическая интерпретация кодового расстояния − это длина кратчайшей цепи, которая соединяет две |
|
вершины n-мерного единичного куба, отвечающие кодовым словам данной схемы. |
|
~ ~ |
~ |
Утверждение. Говорят, что кодовые слова 1, 2 |
,..., s линейно зависимы, если хотя бы одно из них является линейной |
комбинацией остальных слов из этого набора. Если же ни одно из них не является линейной комбинацией остальных слов, то они считаются линейно независимыми.
Определение. Двоичный код называется линейным кодом, если любая линейная комбинация его кодовых слов также является кодовым словом этого кода.
Из определения линейного кода можно получить следующие его свойства:
Любой линейный код содержит нулевое кодовое слово, т.е. слово, состоящее только из нулей.
Кодовые слова линейного кода обязательно линейно зависимы, так как линейный код всегда содержит нулевое
~ ~
слово, а оно выражается через другие кодовые слова с помощью линейной комбинации вида .
Если линейный код не состоит из одного только нулевого слова, то можно так выбрать несколько его линейно независимых кодовых слов, чтобы все кодовые слова являлись линейными комбинациями выбранных слов.
Линейный код размерности r имеет мощность 2r, т.е. содержит ровно 2r кодовых слов.
Кодовое расстояние линейного кода равно минимальному числу единиц в ненулевом кодовом слове этого кода. Определение. Порождающей матрицей линейного кода размерности r с длинами кодовых слов, равными n, называется
матрица размера
Определение.
r на n, в строках которой
Кодовые слова |
~ |
|
стоят базисные кодовые слова этого кода. |
|||||||||||
( |
... |
|
) |
и |
~ |
|
|
|
... |
|
) |
n |
( |
1 |
2 |
n |
|||||||
1 2 |
|
|
|
|
|
|
|
||||
называются
ортогональными, если
|
|
|
2 |
... |
|
n |
1 1 |
2 |
|
n |
|
0
. Каждое слово ортогонально нулевому слову. Кроме того, оно может быть ортогонально и
самому себе. Например, слово (0101) ортогонально словам (0000), (0010), (1000), (1010), (0101), (0111), (1101) и (1111).
Обратим внимание на то, что эти восемь слов образуют линейный код.
Определение. Двойственным кодом к линейному коду Σ называется двоичный код, каждое кодовое слово которого ортогонально любому кодовому слову кода Σ. Двойственный код обладает рядом свойств. Наиболее важное из них состоит в том, что двойственный код к линейному коду размерности r сам является линейным кодом размерности (n – r) , где n – длина кодового слова.
41. Самокорректирующиеся коды (коды Хэмминга), метод построения.
Кодом исходного сообщения может быть любое m-разрядное слово
~ |
|
... |
|
) |
( |
m |
|||
1 |
2 |
|
|
|
в алфавите {0,1}. Множество всех таких
слов образует m-разрядный линейный код мощности 2m. В реальных системах при передаче информации по каналам связи в силу разных причин может происходить искажение сигналов. В результате отдельные разряды передаваемых кодовых слов могут измениться, т.е. ноль может превратиться в единицу, а единица – в ноль. Если искажению подвергся только один разряд передаваемого слова (называется одиночной ошибкой).
В коде Хэмминга используется несколько контрольных разрядов, каждый из них заполняется таким образом, чтобы анализ
их содержимого в случае одиночной ошибки позволил точно определить, в каком именно разряде произошло искажение. |
||||
~ |
|
называются информационными, |
в отличие от контрольных разрядов, |
которые |
Разряды исходного слова ( 1 2... m ) |
|
|||
~ |
|
|
|
|
появляются в передаваемом слове ( 1 2... n ) . |
|
|
||
Также имеет место формула: (m k 1) 2 |
k |
, где m – длина кодового слова, k – число контрольных разрядов. |
|
|
|
|
|||
|
|
~ |
слева направо степенями двойки, т.е. |
числами |
Для удобства будем нумеровать контрольные разряды в кодовом слове |
||||
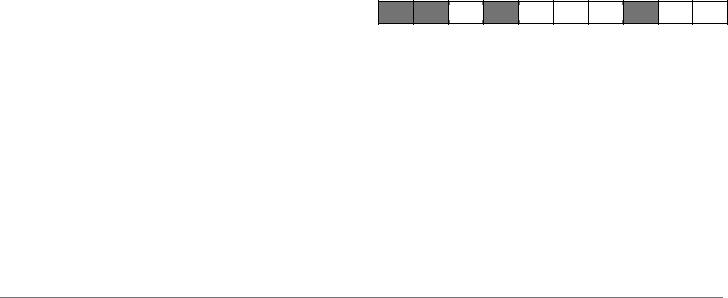
1,2,4,8,…, 2k−1. Остальные позиции содержат информационные разряды. На рисунке изображено кодовое слово с 6 информационными и 4 контрольными разрядами. Все разряды пронумерованы числами от 1 до 10, а контрольные разряды выделены темным цветом.
~
Информационные разряды кодового слова ( 1 2... n )
заполняются слева направо простым переносом символов из
~
исходного слова ( 1 2... m ) . Правило заполнения
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
контрольных разрядов сложнее. Чтобы его сформулировать, рассмотрим множества:
23
V |
|
1 |
|
V |
|
2 |
|
V |
|
4 |
|
V |
|
8 |
|
При
{1, 3, 5, 7, 9,11,...}, |
Эту последовательность множеств можно продолжать |
бесконечно, используя следующую |
|||||
{2, 3, 6, 7,10,11,...}, |
закономерность. Во-первых, номера множеств Vi – это степени двойки. Во-вторых, минимальное |
||||||
{4, 5, 6, 7,12,13,...}, |
число во множестве Vi равно i. В-третьих, множество Vi |
содержит те, и только те натуральные |
|||||
числа, в разложении которых по различным степеням двойки 1,2,4,8,…, i,…, 2k─1 слагаемое i |
|||||||
{8, 9,10,11,12,13,...}. |
|||||||
входит с коэффициентом 1. |
|
|
|
|
|||
|
|
|
~ |
|
|||
заполнении контрольных разрядов |
1, 2 , 4 , 8,..., |
|
|
используются следующие равенства: |
|||
2 |
k 1 |
кодового слова |
|||||
|
|
|
|
|
|
||
1 3 5 7 9 11 ..., 2 3 6 7 10 11 ... , 4 5 6 7 12 13 ... и т.д.
Код Хэмминга позволяет проверять правильность передачи кодовых слов по каналу связи и в случае возникновения одиночной ошибки точно определять её местоположение. Для этого используются так называемые контрольные суммы. У
кода Хэмминга с k контрольными разрядами имеется ровно k контрольных сумм. Обозначим их через Si, где номер i |
||||||
является степенью двойки, т.е. принимает |
значения 1, 2, 4, 8,…, 2k─1. При |
вычислении каждой контрольной |
суммы |
|||
складывается содержимое одного |
из |
контрольных |
и нескольких |
информационных |
разрядов, а |
именно: |
S1 1 3 5 7 9 11 ..., |
S2 2 |
3 6 7 |
10 11 ... , S4 4 5 6 |
7 12 13 ... и т.д. |
||
Указанное правило вычисления контрольных сумм гарантирует, что при передаче кодового слова без искажений все контрольные суммы будут равны нулю. Если же во время передачи кодового слова случится одиночная ошибка, то номер искаженного разряда можно будет легко определить с помощью контрольных сумм. Для этого достаточно вычислить все контрольные суммы (т.е. проверить их на четность) и сложить номера контрольных сумм, отличных от нуля.
Пример 1. Исходные слова |
~ |
имеют длину 5. Требуется выяснить, какую длину будут иметь кодовые слова кода Хэмминга. |
|||||||
|
|
||||||||
По условию |
задачи m = 5. |
Поэтому определим |
число контрольных |
разрядов |
k из |
неравенства (52), |
переписав его в |
||
следующем |
виде: (6 k) 2 |
k |
. Последовательно |
подставляя вместо |
k числа |
1,2,3 |
и т.д., выясняем, |
что наименьшее |
|
|
|||||||||
допустимое значение k равно 4. Значит, кодовые слова кода Хэмминга в данном случае имеют длину n = m + k = 9.
|
|
|
|
|
|
|
|
|
~ |
|
|
Пример 2. Требуется построить кодовое слово кода Хэмминга, соответствующее исходному слову (001011) . |
|
|
|||||||||
Прежде всего заметим, что при шести информационных разрядах количество контрольных разрядов k должно быть равно |
|||||||||||
четырем. Следовательно, кодовое слово будет состоять из |
|
|
|
|
|
|
|||||
десяти разрядов. Сначала заполним его информационные |
0 |
0 |
1 |
0 |
1 |
1 |
|||||
разряды. |
Получим |
слово, |
изображенное |
на |
рисунке |
|
|
|
|
|
|
(контрольные разряды выделены темным цветом). |
|
|
|
|
|
|
|
||||
Теперь в соответствии с указанным выше правилом заполним контрольные разряды:
1 0 0 0 1 1, 2 0 1 0 1 0 |
, |
4 0 1 0 1 |
, 8 9 10 1 1 0 |
В итоге получаем искомое кодовое слово |
~ |
|
|
(1001010011) . |
|
||
.
Пример 3. На выходе канала связи получили кодовое слово кода Хэмминга
~
(1001011101)
. Требуется выяснить, какое
слово |
~ |
было отправлено. |
|
Найдем контрольные суммы. Их будет столько же,
S1 1 0 0 1 0 0 , S2 0 0 1 1 1 1 ,
сколько и контрольных разрядов,
S4 1 0 1 1 1 |
, S8 1 0 1 |
т.е. четыре. Получим
0 .
Отличными от нуля оказались контрольные суммы S2 и S4. Складывая их номера, узнаём, что одиночная ошибка произошла |
|||
~ |
|
~ |
|
. Исправив в этом разряде единицу на ноль, получим отправленное слово |
(1001001101) . |
||
в шестом разряде слова |
|||
Теория автоматов
42. Определение, схема и функционирование абстрактного автомата, способы задания автоматов.
Устройство, обрабатывающее информацию, обменивается ею с внешней средой через входной и выходной каналы, по которым поступает информация – входные сигналы – и выдается результат обработки этой информации – выходные сигналы. Кроме этого, устройство, как правило, имеет память, содержимое которой во время работы устройства может меняться. Эти изменения зависят, с одной стороны, от содержимого памяти в данный момент времени, а с другой стороны, от входного сигнала, поступившего в этот момент по входному каналу. Содержимое памяти реального устройства - состояние автомата. Выходной сигнал в каждый момент времени также зависит от входного сигнала и от состояния автомата в настоящий момент.
Определение. Поступление входного сигнала, переход автомата из одного состояния в другое и выдача выходного сигнала происходят дискретно и мгновенно в определенные моменты времени, эти моменты времени следуют один за другим через фиксированный промежуток времени – такт.
Определение. Входной алфавит A – это конечное множество А = {а1, а2, …, аs}, элементы которого называются входными сигналами (символами).
Определение. Выходной алфавит В = {b1, b2, …, bk} – это множество выходных сигналов (символов).
24

В каждый момент времени t = 1, 2, 3, … на вход автомату подается некоторый сигнал из множества А, а на выходе |
|||||||||||
появляется соответствующий сигнал из множества В. Тогда, учитывая описанный выше потактовый принцип работы |
|||||||||||
абстрактного автомата, входной сигнал в момент времени t будем обозначать через x(t), а в следующий момент – через |
|||||||||||
x(t + 1). Соответствующие выходные сигналы обозначим через у(t) и у(t + 1). |
|
|
|
||||||||
Множество состояний – это конечное множество V = {v1, v2, …, vr}. Состояние автомата в момент времени t будем |
|||||||||||
обозначать через q(t). Напомним, что состояние автомата – это состояние (содержимое) его памяти. Таким образом, |
|||||||||||
существенными составляющими любого автомата являются входной и выходной алфавиты А и В, а также множество |
|||||||||||
состояний V. |
|
|
|
|
|
|
|
|
|
|
|
Схема |
и |
функционирование |
абстрактного |
|
|
|
|
||||
автомата. На рисунке структура абстрактного |
Входной |
|
|
Выходной |
|||||||
автомата. |
За |
один |
такт |
его |
работы |
происходят |
Функциональный |
||||
следующие события. В момент времени t (начало t-го |
x(t) |
|
блок |
y(t) |
|||||||
канал |
|
канал |
|||||||||
такта) в функциональный блок синхронно поступают |
|
|
q(t) |
|
|||||||
два сигнала: x(t) – по входному каналу и q(t – 1) – из |
|
q(t-1) |
|
||||||||
памяти автомата. В функциональном блоке эти |
|
|
|
|
|||||||
сигналы мгновенно перерабатываются в два новых |
|
|
Память |
|
|||||||
сигнала у(t) и q(t). Сигнал у(t) направляется в |
|
|
|
|
|||||||
выходной канал, а сигнал q(t) – в память автомата. |
|
|
|
|
|||||||
После этого наступает момент времени t + 1, который служит одновременно окончанием t-го такта и началом следующего |
|||||||||||
(t + 1)-го такта. Поскольку первый такт начинается в момент времени t = 1, то сигнал q(0), поступающий в этот момент из |
|||||||||||
памяти автомата в функциональный блок, характеризует начальное состояние автомата, которое обычно считается |
|||||||||||
известным заранее (например, можно считать, что автомат стартует с «чистой» памятью). Пару сигналов (x(t), q(t – 1)) |
|||||||||||
можно сравнить со «стимулом» в момент времени t, а пару (у(t), q(t)) – с мгновенной «реакцией» автомата на этот «стимул». |
|||||||||||
Определение. Автомат называется детерминированным, если для любых t |
и t´ |
из равенств x(t) = x(t´) и q(t – 1) = q(t´– 1) |
|||||||||
следуют |
равенства |
y(t) = y(t´), q(t) = q(t´). Свойство |
детерминированности |
автомата означает, |
что принципы его |
||||||
функционирования с течением времени не меняются. |
|
|
|
|
|||||||
Определение. Функцией выходов автомата называется функция f, которая каждой паре (ai, vj), где ai А, vj V, ставит в |
|||||||||||
соответствие выходной сигнал f(ai, vj) |
|
В. Функция выходов указывает, какой сигнал будет направлен на выход автомата, |
|||||||||
если он находился в состоянии vj, и на вход ему поступил сигнал ai. |
|
|
|
||||||||
Определение. Функцией переходов автомата называется функция g, которая каждой паре (ai, vj), где ai А, vj V, ставит в |
|||||||||||
соответствие состояние g(ai, vj) V.Функция переходов указывает, в каком состоянии окажется автомат, если он находился в |
|||||||||||
состоянии vj, и на вход ему поступил сигнал ai. |
|
|
|
|
|||||||
С помощью набора правил функционирования. |
|
|
|
|
|||||||
(а1, v1) → (b1, v1), (а1, v2) → (b1, v2), (а2, v1) → (b2, v1), (а2, v2) → (b1, v1),
(а3, v1) → (b3, v2), (а3, v2) → (b3, v2).
С помощью таблицы. Чтобы задать автомат табличным способом,
надо заполнить его таблицу выходов и переходов, исходя из функции выходов f и функции переходов g. В крайнем левом столбце таблицы перечислены символы входного алфавита А = {а1, а2, …, аs}, а в верхней строке – элементы множества состояний V = {v1, v2, …, vr}. В клетке, стоящей на пересечении строки ai и столбца vj, стоит пара f(ai, vj), g(ai,
|
v1 |
… |
vr |
a1 |
f(a1,v1), g(a1,v1) |
… |
f(a1,vr), g(a1,vr) |
… |
|
… |
|
|
|
|
|
as |
f(as,v1), g(as,v1) |
… |
f(as,vr), g(as,vr) |
vj), которая согласно определению функций f и g указывает, что если автомат находился в состоянии vj и на вход ему подали сигнал ai, то на выходе автомата получим сигнал f(ai, vj), и автомат перейдет в состояние g(ai, vj). Используя такую таблицу, можно для любой последовательности входных сигналов определить, как будет выглядеть соответствующая последовательность выходных сигналов или состояний автомата.
Спомощью диаграммы Мура. При таком способе автомат
изображается в виде ориентированного графа, в котором допускаются |
(a, a) |
|
(a, a) |
|
кратные дуги и петли. Число вершин равно r − числу состояний автомата. |
(c, c) |
|||
|
|
|||
Каждая вершина помечена символом из множества состояний V = {v1, v2, |
|
|
v2 |
|
…, vr}. Дуга выходит из вершины vk в вершину vn тогда и только тогда, |
v1 |
|
||
|
|
|
когда в данном автомате возможен переход из состояния vk в состояние vn по некоторому входному сигналу. Все дуги, выходящие из вершины
vk, помечены парой символов вида (ai, bj), где ai А, bj = f(ai, vk). Иными
словами, начало дуги определяет состояние автомата в предшествующий, а её конец – в последующий моменты времени. При этом на самой дуге указывается входной и соответствующий ему выходной сигналы. Граф диаграммы Мура должен удовлетворять условию детерминированности. Оно заключается в том, что для любого входного символа ai из каждой вершины должна выходить только одна дуга, помеченная этим символом. Поэтому в диаграмме Мура из каждой вершины выходит ровно s дуг, где s – это мощность алфавита А.
25
43. Типы конечных автоматов, автоматы Мили и Мура, автоматы-генераторы.
Определение. Конечным автоматом (или автоматом Мили) называется система из пяти компонент (А, В, V, f, g), где А и В
– это входной и выходной алфавиты автомата, V – множество его состояний, f – функция выходов, а g – функция переходов автомата, причем все множества А, В и V конечны.
Определение. Любую конечную последовательность символов из входного или выходного алфавитов называются соответственно входным и выходным словом. Множество всех входных слов обозначим через А*.
Определение. Любое подмножество множества А* называется языком.
Автоматы-распознаватели, автоматы-преобразователи и автоматы-генераторы – конечные детерминированные автоматы. Автоматы-распознаватели. Основной особенностью этих автоматов является то, что множество их состояний V всегда разбивается на два непересекающихся класса: F и V \ F. Все состояния из класса F считаются особыми и называются заключительными состояниями. Если на вход такому автомату подать слово w, составленное из символов алфавита А, то может оказаться, что автомат завершит работу в одном из заключительных состояний. В этом случае будем говорить, что автомат распознает данное слово w. Все слова, которые распознает автомат, образуют подмножество множества А*, т.е. составляют некоторый язык L. Тогда про язык L говорят, что он распознается этим автоматом, или что данный автомат распознает язык L. Поскольку считается, что такой автомат распознает слово w только тогда, когда он завершает работу над этим словом в одном из заключительных состояний, то о результате работы автомата мы судим лишь по его состоянию в момент завершения работы. При этом выходные символы, возникающие в процессе функционирования таких автоматов, особого значения не играют. Следовательно, можно игнорировать выходные сигналы или вообще убрать выходной канал. Поэтому автоматы-распознаватели иногда ещё называют автоматами без выходов. Их функционирование можно описать только одной функцией – функцией переходов. Из этого следует, что автомат-распознаватель – это система из четырех компонент : (А, V, F, g), где А – входной алфавит, V – множество всех состояний, F – множество заключительных состояний, а g – функция переходов. В диаграмме Мура такого автомата уже не нужно указывать выходные сигналы, а его таблица выходов и переходов преобразуется в более простую таблицу переходов.
Автоматы-преобразователи. В отличие от автоматов-распознавателей у них всегда задана функция выходов f. Автоматыпреобразователи посимвольно прочитывают входную последовательность и перерабатывают её в выходную последовательность такой же длины. Например, с их помощью можно моделировать процессы алфавитного кодирования информации. Любой автомат-распознаватель нетрудно превратить в автомат-преобразователь. Для этого достаточно считать, что выходной сигнал в конце каждого такта совпадает с входным сигналом в начале этого же такта, т.е. y(t) = x(t). Полученный таким образом автомат-преобразователь можно использовать для генерации слов, принадлежащих тому языку, который распознавался исходным автоматом-распознавателем. Когда мы рассматриваем какой-либо конкретный автоматпреобразователь, нам в первую очередь важно знать, какая последовательность получается на выходе этого автомата при заданной входной последовательности. Когда же мы исследуем автомат-распознаватель, нам важно знать лишь состояние, в котором этот автомат закончил работу над заданным словом. Таким образом, автоматы-преобразователи лучше подходят для описания вычислительных устройств, а автоматы-распознаватели – для описания устройств управления.
Среди автоматов-преобразователей особо выделяют автоматы Мура. Это автоматы, у которых функция выходов f не зависит от входного сигнала, т.е. f(ai, vj) = f(ak, vj) = bj В для всех ai, ak А и vj V. У автомата Мура для каждого t выход y(t) может зависеть от состояния автомата в начале этого t–го такта, т.е. от q(t – 1), но не должен зависеть от входного сигнала x(t). Образно говоря, выходные сигналы автомата Мура зависят от входных сигналов лишь с «запаздыванием».
В отличие от автомата Мили, в диаграмме автомата Мура метка на дуге – это не пара символов ai и f(ai, vj), а только один входной символ ai. При этом символом f(ai, vj) помечается сама вершина vj. Это объясняется тем, что, согласно определению автомата Мура, выходной символ f(ai, vj) совпадает у всех дуг, выходящих из одной и той же вершины vj. В следующем примере рассматривается простейший автомат Мура, который часто используется в качестве строительного блока для более сложных автоматов.
Автоматы-генераторы. Автономный автомат (автомат-генератор) – это автомат без входа. Он полностью определяется системой из пяти компонент (В, V, F, f, g), где В – выходной алфавит, V – множество всех состояний, F – множество заключительных состояний, а f и g – функции выходов и переходов, причем f и g являются функциями только одного аргумента – состояния автомата. Генераторы используются, например, для порождения символьных строк в алфавите В. Слово, порожденное автономным автоматом, – это последовательность выходных сигналов, которая образуется при завершении работы автомата в любом из заключительных состояний. Далее мы увидим, что при фиксированном начальном состоянии выходное слово, порожденное генератором, зависит лишь от продолжительности его работы. Меняя начальное состояние и (или) число рабочих тактов, можно породить некоторый язык из В*, т.е. набор слов в алфавите В.
Логические автоматы. Автоматы, у которых входной и выходной алфавиты и множество состояний образованы наборами из нулей и единиц фиксированной длины. Благодаря этому функции переходов и выходов автомата f и g можно считать логическими (булевыми) функциями. Схема из функциональных элементов – дизъюнкторов, конъюнкторов и инверторов – это логический автомат без памяти и, следовательно, с одним состоянием. Функциональный блок любого логического автомата можно «синтезировать» из функциональных элементов, а его память – из рассмотренных выше единичных задержек.
44. Слова и языки, операции над ними, их свойства.
Определение. Входное слово – произвольная строка конечной длины, составленная из символов входного алфавита А. У таких автоматов одно или несколько состояний заранее объявляются заключительными. Считается, что автомат распознал слово, поданное ему на вход, тогда и только тогда, когда он завершил работу над этим словом в одном из своих заключительных состояний.
26

Определение. Язык – множество всех слов, распознаваемых автоматом. Сам язык может быть как конечным, так и бесконечным, но в любом случае он состоит только из слов, распознаваемых соответствующим автоматом.
Определение. Суммой языков L и L´ называется язык, который обозначается L + L´ и получается объединением множеств L
и L´, т.е. L + L´ = {w |
|
w L L } . |
Определение. Произведением языков L и L´ называется язык, который обозначается L·L´ и получается в результате
конкатенации всех возможных слов w и w´, где w принадлежит языку L, а w´ – языку L´, т.е. L·L´ =
{ww 
w L,
w
L }
.
Заметим, что язык L·L´, как правило, отличается от языка L´·L, хотя некоторые слова могут принадлежать обоим произведениям.
Определение. Итерацией языка L называется язык, который обозначается L* и получается в результате сложения
бесконечного числа языков {Λ} + L + L2 + L3 + … + Lk + …, т.е. L* =
Lk .
k 0
Итерация выражается через операции сложения и умножения языков. Из всех введенных операций над языками она единственная, которая позволяет из конечного языка получить бесконечный.
Таким образом, с помощью введенных операций сложения, умножения и итерации некоторые языки можно выражать в виде формул через более простые языки. Причем результатом сложения или умножения двух конечных языков всегда будет конечный язык, и лишь итерация позволяет из конечного языка получить бесконечный. Некоторые важные свойства операций над языками:
1. L1· (L2 + L3) = L1· L2 + L1· L3; |
5. L· Λ = L; |
||
2. (L1 + L2) · L3 = L1· L3 + L2· L3; |
6. L· L* = L*· L; |
||
3. |
L + L = L; |
7. |
Λ + L· L* = L*; |
4. |
L + L* = L*; |
8. |
((L1)*· (L2)*)* = (L1 + L2)*. |
Пустое подмножество множества А*, как и всякое другое его подмножество, тоже считается языком. Этот язык мы будем называть пустым языком и обозначать символом пустого множества . Очевидно, что для любого языка L верны равенства
L + = L и L· = . Значит, при всех натуральных значениях n выполняется n = . Тогда из определения операции итерации получаем * = Λ + + 2 + 3 + … + n + … = Λ.
Заметим также, что Λ* = Λ, поскольку Λn = Λ и Λ + Λ = Λ.
Определение. Пусть имеется алфавит А = {а1, а2, …, аs}. Одноэлементные языки а1, а2, …, аs, а также язык, содержащий только пустое слово Λ - элементарные языки.
45. Регулярные выражения и регулярные языки, теорема Клини.
Определение. Регулярным языком называется такой язык, который можно получить из элементарных языков с помощью конечного числа операций сложения, умножения и итерации.
Чтобы доказать регулярность какого-либо языка, надо записать его в виде так называемого регулярного выражения, т.е. формулы, в которой конечное число раз используются элементарные языки и знаки операций сложения, умножения и итерации. Поскольку количество регулярных выражений счетно, то число различных регулярных языков не более, чем счетно. Всего же имеется континуум языков над фиксированным конечным алфавитом А, т.к. язык – это любое подмножество счетного множества А*. Следовательно, существуют и нерегулярные языки.
Пример. Рассмотрим несколько языков.
1)Конечный язык L1 = {a, ab, abc} является регулярным языком, т.к. его можно задать равенством L1 = a + ab + abc = a + a·b + a·b·c = a·(Λ + b·(Λ + c)). Последнее полученное выражение является регулярным, поскольку оно содержит только простейшие языки a, b, c и Λ и конечное число знаков операций сложения и умножения. Этот пример показывает, что любое конечное множество слов образует регулярный язык.
2)Бесконечный язык L2 = {с, cabc, cabcabc, cabcabcabc, …}, порождаемый автоматом из примера 4 §3, является регулярным, т.к. его можно задать разными регулярными выражениями: с·(a·b·с)*, либо (с·a·b)*·с. Этот пример свидетельствует о том, что один и тот же язык можно представить через различные регулярные выражения.
3)Бесконечный язык L3, состоящий из всех слов конечной длины в алфавите А = {a, b, c}, включая и пустое слово, является регулярным языком, поскольку выполняется равенство L3 = (a + b + с)*.
4)Бесконечный язык L4 над алфавитом А = {a, b, c}, образованный словами, которые содержат хотя бы одну букву с, регулярен, т.к. он может быть задан равенством L4 = (a + b + с)*· с· (a + b + с)*.
5)Бесконечный язык L5 над алфавитом А = {0,1}, образованный всеми словами, кроме слов 0 и 11, регулярен, т.к. его можно задать регулярным выражением Λ + 1 + 00 + 01 + 10 + (0 + 1)3 · (0 + 1)*.
6)Бесконечный язык L6 = {1, 10, 101, 1010, 10100, …}, состоящий из всех начальных отрезков {а1, а1а2, а1а2а3, …}
бесконечной последовательности (10100100010…), не является регулярным.
Определение. Пересечением языков L и L´ называется язык, который обозначается L ∩ L´ и состоит из всех слов, принадлежащих одновременно обоим языкам L и L´. Поскольку всякий язык является подмножеством множества А* всех слов конечной длины в некотором фиксированном алфавите А, то пересечение языков – это обычная операция пересечения множеств слов.
Определение. Дополнением языка L в алфавите А называется язык, который обозначается L и состоит из слов множества А*, не принадлежащих языку L. Язык L и его дополнение L не имеют общих слов, а их сумма совпадает с множеством А*.
27

Операция пересечения языков не относится к числу основных, поскольку она
сложения и дополнения. Действительно, из закона де Моргана следует, что |
L1 L2 |
может
L |
L |
1 |
2 |
быть выражена через операции
.
Пример. Пусть исходный язык L состоит из всех таких слов в алфавите А = {0,1}, которые начинаются с нуля, а оканчиваются двумя единицами. Нетрудно проверить, что этот язык можно задать регулярным выражением 0· (0 + 1)*· 11. Тогда дополнительный к нему язык L состоит из всех таких слов в алфавите А, которые начинаются с единицы или оканчиваются любой из трех комбинаций – 00, 01 или 10. Язык L можно задать регулярным выражением 1· (0 + 1)* + (0 + 1)*· (0· 0+ 0· 1 + 1· 0).
При фиксированном алфавите А класс регулярных языков над А замкнут относительно всех перечисленных выше операций
– сложения, умножения, итерации, пересечения и дополнения. Это означает, что язык, получаемый в результате применения данных операций к регулярным языкам, тоже является регулярным.
Существует тесная связь между регулярными языками и конечными автоматами. Дело в том, что, с одной стороны, любой регулярный язык обязательно распознается некоторым конечным детерминированным автоматом (автоматом Мили). А с другой стороны, автоматы Мили способны распознавать только регулярные языки. Оба эти утверждения сформулированы в основной теореме теории автоматов (теореме Клини).
Теорема Клини. Язык L распознается конечным детерминированным автоматом тогда и только тогда, когда L – регулярный язык.
46. Задача анализа автоматов-распознавателей.
Задача анализа автомата состоит в том, чтобы для конкретного автомата найти язык, распознаваемый этим автоматом. Опишем алгоритм, использующий квадратные матрицы r-го порядка С0, С1, С2, …, Сr (где r – число состояний автомата),
элементами которых являются регулярные выражения. Элементы матрицы Сk обозначим через |
k |
cij . Для каждой пары (i, j), |
|
0 |
|
где i, j = 1, 2, …, r, элемент cij матрицы С0 – это множество тех символов входного алфавита А, каждый из которых за один |
|
0 |
можно задать регулярным |
такт переводит автомат из состояния vi в состояние vj. Поскольку это множество конечно, то cij |
|
выражением.
c |
k |
c |
k 1 |
c |
k 1 |
|
ij |
ij |
ik |
||||
|
|
|
Элементы
(c |
k 1 |
) * c |
|
kk |
|||
|
|
матриц С1, С2, …, Сr будем вычислять с помощью рекуррентного соотношения |
|
k 1 |
. |
kj |
|
Из этого соотношения следует, что если все элементы матрицы Сk–1 – регулярные выражения, то матрица Сk тоже будет
состоять из регулярных выражений. Можно строго доказать, что для любого k = 1, 2, …, r элемент |
k |
представляет собой |
cij |
множество всех входных слов, переводящих автомат из состояния vi в состояние vj за несколько тактов, но так, чтобы при
этом автомат не проходил через промежуточные состояния, номера которых превосходят k. Если считать, что v1 – начальное |
|||||
состояние автомата, а F – множество всех заключительных состояний, то язык L, распознаваемый этим автоматом, можно |
|||||
|
1 j |
|
|||
будет задать в виде суммы регулярных выражений L |
|
|
c |
r |
, где суммирование ведется по всем заключительным |
|
|
|
|||
|
v |
j |
F |
|
|
|
|
|
|
|
|
состояниям автомата.
Пример 1. Пусть автомат с начальным состоянием v1 и заключительным состоянием v3 задан диаграммой Мура. Дуга, помеченная выражением a + b, заменяет пару параллельных дуг из v3 в v3, одна из которых имеет метку a, а другая – метку b. Требуется получить регулярное выражение для языка L, распознаваемого этим автоматом. Матрица С0 легко
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
|
|
|
|
получается из диаграммы Мура. В данном случае она имеет вид |
|
|
b |
a |
|
. |
|
||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a b |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Равенство |
1 |
a b |
означает, что из состояния v3 в состояние v3 автомат может попасть за |
||||||||||||||
c33 |
|||||||||||||||||
один такт либо по слову а, либо по слову b. |
|
|
|
|
|
|
|
|
|
|
|
||||||
Элементы |
1 |
матрицы С1, где i, j = 1, 2, 3, находим через известные элементы матрицы С0, |
|||||||||||||||
cij |
|||||||||||||||||
используя |
рекуррентные |
1 |
0 |
0 |
0 |
0 |
|
|
Поскольку |
|
0 |
, то |
|||||
соотношения cij |
cij |
ci1 |
(c11) * c1 j . |
|
|
c11 |
|||||||||||
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
cij cij ci1 Λ c1 j cij |
ci1 |
c1 j . |
|
|
|
|
|
|
|
|
|
|
|
||||
|
v2 |
b |
a |
|
a |
|
|
v3 |
v1 |
b |
|
|
|
a+b |
0 |
Следовательно, |
|
(c11)* Λ . |
||
Например, |
c1 |
c0 |
c0 |
c0 |
a a a a. |
Вычислив остальные элементы матрицы С1, получаем, чтоС1 = |
|
12 |
12 |
11 |
12 |
|
|
|
|
a |
|
|
|
b |
|
|
|
|
|
|
|||
|
|
||
что |
c122 |
||
b |
|
|
|
|
|
|
a |
|
. Элементы матрицы С2 |
||||
|
|
|
|
|
|
|
a b |
|
|
|
|
|
|
b , |
получаем |
2 |
1 |
1 |
b * |
|
cij |
cij ci2 |
|||||
находим из рекуррентных соотношений
1 |
2 |
1 |
1 |
1 |
b |
c2 j . Например, |
c13 |
c13 |
c12 |
b* c23 |
cij2
a
c1ij c1i2 (c122 ) * c12 j ,откуда, учитывая,
b * a . Это равенство означает, что из
состояния v1 в состояние v3 автомат может попасть либо за один такт по слову b, либо за несколько тактов по слову, которое начинается и оканчивается символом а, а между ними возможно многократное повторение символа b. Это согласуется с диаграммой Мура данного автомата. Таким образом находим все элементы матрицы С2. В итоге получаем
|
|
a a b * b |
b a b * a |
||
|
|
|
|
|
|
С2 |
= |
|
b b b * b |
a b b * a . |
|
|
|
|
|
a b |
|
|
|
|
|||
|
|
|
|
||
28
Некоторые элементы матрицы С2 можно упростить, используя свойства операций над языками:
a + a·b*·b = a·(Λ + b*·b) = a·b*, |
|
||||
b + b·b*·b = b·(Λ + b*·b) = b·b*, |
|
||||
a + b·b*·a = (Λ + b·b*)·a = b*·a. |
|
||||
В итоге получим упрощенную матрицу С2 |
|
|
|
|
|
|
a b * |
b a b * a |
|
||
|
|
b b * |
b * a |
|
|
С2 = |
. |
|
|||
|
|
|
a b |
|
|
|
|
|
|||
|
|
|
|
||
Согласно алгоритму, регулярное выражение для языка L, распознаваемого данным автоматом, будет равно элементу |
3 |
||||
c13 |
|||||
матрицы С3. Поэтому нет необходимости искать всю эту матрицу, а достаточно лишь найти указанный элемент. Используя
рекуррентные соотношения |
3 |
2 |
2 |
2 |
2 |
3 |
2 |
2 |
2 |
2 |
|
cij |
cij |
ci3 |
(c33 ) * c3 j , получаем c13 |
c13 |
c13 |
(c33 ) * c33 |
|||||
(b a b * a) (b a b * a) (a b) * (a b) |
(b a b* a) (Λ (a b) * (a b)) (b a b* a) (a b)* . |
||||||||||
Таким образом, язык L можно задать регулярным выражением (b + a·b*·a)·(a + b)* = b·(a + b)* + a·b*·а·(a + b)*.
В итоге мы получили сумму двух регулярных выражений. Слагаемое b·(a + b)* задает все слова в алфавите {a, b}, начинающиеся с буквы b. Слагаемое a·b*·а·(a + b)* описывает слова, которые начинаются с буквы а, причем она должна встречаться в слове не менее двух раз. Только два указанных типа слов распознаются заданным автоматом. Такой окончательный вывод согласуется с диаграммой Мура.
Пусть автомат, распознающий некоторый язык L, задан диаграммой Мура. Решив задачу анализа для этого автомата, мы получим регулярное выражение, задающее язык L. Спрашивается, каким регулярным выражением можно задать
дополнительный язык
L
? Рассмотрим два автомата, один из которых распознает L, а другой –
L
. Поскольку всякое слово
из множества А* обязательно принадлежит одному из языков L или L (но не обоим сразу!), то каждое слово распознается каким-либо одним этих автоматов, но не распознается другим. Следовательно, оба автомата задаются одинаковыми диаграммами Мура и имеют одно и то же начальное состояние. Отличаются они лишь тем, что каждое заключительное состояние одного из автоматов считается незаключительным состоянием для другого автомата. Поэтому, изменив набор заключительных состояний в диаграмме Мура, задающей автомат для распознавания L, мы получим диаграмму автомата,
распознающего L . Например, если в автомате из примера 1, распознающем язык L, объявить v1 |
начальным состоянием, а v1 |
|||||
и v2 – заключительными, то полученный автомат будет распознавать дополнительный язык |
L . Затем, решив для него задачу |
|||||
|
|
|
|
|
|
|
анализа, найдем регулярное выражение для L . |
|
|
|
|
||
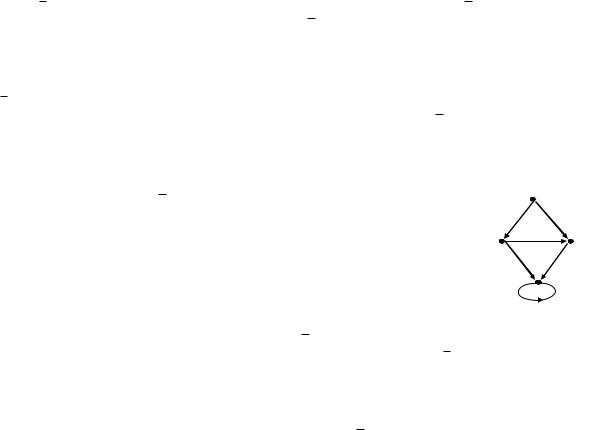
Пример 2. Пусть автомат с начальным состоянием v1 и заключительными состояниями v2 |
и v3 |
|
|
|||
задан диаграммой Мура. Найдем регулярное выражение для языка L, распознаваемого этим |
v1 |
|
||||
автоматом, а также дополнительного языка L . |
|
|
|
|||
|
|
|
|
|||
Поскольку в диаграмме Мура данного автомата ни один ориентированный путь из начальной |
0 |
1 |
||||
вершины в заключительную не содержит ориентированных циклов, |
то L –конечный язык. |
0 |
v3 |
|||
|
|
|
|
|
||
Заметим также, что единственный ориентированный путь из v1 в v2 |
состоит из одной дуги |
v2 |
||||
|
|
|||||
[v1, v2], помеченной символом 0. Поэтому слово 0 распознается данным автоматом. Кроме того, |
1 |
0+1 |
||||
имеется два ориентированных пути из v1 в v3. Один путь – это дуга [v1, v3], помеченная |
|
|
||||
символом 1, а другой – последовательность дуг [v1, v2], [v2, v3], каждая из которых содержит |
v4 |
0+1 |
||||
метку 0. Следовательно, автомат распознает ещё два слова: 1 и 00. Таким образом, язык L можно |
|
|
||||
задать регулярным выражением 0 + 1 + 0· 0.
Чтобы получить регулярное выражение для дополнительного языка
L
, заключительными состояниями автомата объявим v1
и v4. Поскольку v1 является одновременно и начальным, и заключительным состоянием, то L содержит пустое слово Λ. В диаграмме Мура найдем сначала все ориентированные пути конечной длины из начального состояния в заключительное. Один такой путь образован дугами [v1, v2] и [v2, v4], что соответствует слову 01. Второй путь состоит из дуг [v1, v3] и [v3, v4] и задает регулярное выражение 1·(0 + 1). Третий путь состоит из дуг [v1, v2], [v2, v3], [v3, v4]. Он распознает регулярное выражение 0·0·(0 + 1). Кроме того, есть ещё бесконечное множество путей, которые получаются из трех указанных путей добавлением к ним в конце произвольного числа петель [v4, v4]. Значит, язык L можно задать регулярным выражением Λ +
(0·1 + (1 + 0·0)·(0 + 1))·(0 + 1)*.
47. Задача синтеза автоматов-распознавателей.
Задача синтеза состоит в том, чтобы для заданного языка L построить (синтезировать) автомат, распознающий этот язык. Согласно основной теореме теории автоматов, такой автомат существует только тогда, когда L – регулярный язык. Поэтому далее будем решать задачу синтеза в предположении, что исходный язык L задан регулярным выражением.
Напомним, что диаграмма Мура детерминированного автомата удовлетворяет условию детерминированности, т.е. для любого символа входного алфавита А из каждой вершины должна выходить ровно одна дуга, помеченная этим символом. Далее нам потребуются ориентированные графы, напоминающие диаграмму Мура автомата-распознавателя, но не обязательно обладающие свойством детерминированности. Такие графы мы будем называть недетерминированными источниками. Недетерминированный источник отличается от диаграммы Мура тем, что из любой его вершины может выходить несколько дуг, помеченных одним и тем же входным символом, или не выходить ни одной дуги с этим символом.
29

Кроме того, некоторые дуги источника могут быть пустыми, т.е. помеченными символом Λ. Устройство, описываемое недетерминированным источником, является недетерминированным автоматом. Его также будем называть недетерминированным источником (или просто источником). Очевидно, любой детерминированный автомат является источником, но не любой источник можно считать детерминированным автоматом из-за того, что в источнике может быть нарушено условие детерминированности. Источник, как и автомат-распознаватель, имеет одну начальную и одну или несколько заключительных вершин. Поэтому он тоже распознает некоторый язык.
ТЕОРЕМА. Если недетерминированный источник имеет n состояний и распознает некоторый язык L, то найдется детерминированный автомат, который имеет не более 2n состояний и распознает тот же самый язык L.
Из этой теоремы следует, что недетерминированные источники способны распознавать только регулярные языки. Более того, теорема утверждает, что для любого источника найдется эквивалентный ему автомат, т.е. автомат, распознающий тот же самый язык. Иными словами, в области распознавания языков детерминированные автоматы умеют выполнять ту же самую работу, что и недетерминированные источники. Теорема об источнике дает нам метод для решения задачи синтеза автомата. Действительно, сначала по заданному языку можно построить недетерминированный источник (это сделать проще, чем сразу строить детерминированный автомат), а затем полученный источник надо преобразовать в эквивалентный ему детерминированный автомат.
s |
u1 |
v1 |
t |
|
|
G1 |
|
«детерминизировать», т.е.
Алгоритм построения источника по заданному языку опирается на тот факт, что для любого регулярного языка существует распознающий его двухполюсный источник, т.е. источник с одной начальной и одной заключительной вершинами. Это позволяет строить требуемый источник последовательным и (или) параллельным соединением более простых источников, распознающих отдельные множители и слагаемые, входящие в состав заданного регулярного выражения. А именно, пусть имеются два двухполюсных источника G1 и G2, распознающие языки L1 и L2. Через u1, u2 и v1, v2 обозначим соответственно их начальные и заключительные вершины. Параллельное соединение этих источников изображено на рисунке «а». Все добавленные дуги являются пустыми, т.е. помечены символом Λ. Добавленные вершины и и v являются начальной и заключительной вершинами полученного источника соответственно. Очевидно, этот источник распознает сумму языков L1 + L2.
u1 |
|
v1 |
|
|
|
|
Последовательное соединение двухполюсников G1 |
||||
G1 |
|
|
|
|
и G2 изображено на |
рисунке |
«б». При |
||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
последовательном соединении добавляется пустая |
|||||
|
|
|
|
u2 |
|
v2 |
|||||
u |
|
v |
G1 |
G2 |
дуга, идущая из заключительной вершины первого |
||||||
|
v1 |
|
|||||||||
|
|
|
u1 |
|
|
источника |
в |
начальную |
вершину второго |
||
|
G2 |
|
|
|
|
|
|||||
u2 |
v2 |
|
|
|
|
источника. |
В |
полученном источнике начальной |
|||
|
|
|
|
|
|||||||
|
|
|
|
|
вершиной является u1, |
а заключительной |
|||||
|
a) |
|
|
б) |
|
|
|||||
|
|
|
|
|
вершиной – v2. Этот |
источник |
распознает |
||||
|
|
|
|
|
|
|
произведение языков L1· L2. |
|
|
||
Чтобы из двухполюсника G1 |
получить источник, распознающий итерацию языка (L1)*, необходимо выполнить следующие |
||||||||||
действия: добавить новые начальную и заключительную вершины s и t; провести пустые дуги [s, t], [s, и1], [v1, u1], [v1, t]. В итоге получим двухполюсный источник с начальной вершиной s и заключительной вершиной t.
Пример 1. Имеется язык L, заданный регулярным выражением ab + с*. Требуется построить источник, распознающий язык
L.
Синтаксический анализ заданного регулярного выражения показывает, что оно состоит из двух слагаемых. Поэтому достаточно построить двухполюсные источники отдельно для каждого слагаемого, а затем подключить их параллельно. Поскольку первое слагаемое – это произведение двух множителей a и b, то распознающий его двухполюсный источник G1
v1 а |
b |
v3 |
получается последовательным соединением двух простейших двухполюсников, построенных |
|||
отдельно для каждого слагаемого. В источнике G1 |
вершина v1 |
является начальной вершиной, а v3 |
||||
|
v2 |
|
||||
|
|
– заключительной. Заметим, что согласно правилу последовательного соединения |
||||
|
|
|
||||
|
|
|
двухполюсников в источнике G1 следовало бы |
провести |
пустую дугу из заключительной |
|
вершины первого двухполюсника в начальную вершину второго двухполюсника. Однако вместо добавления пустой дуги мы просто отождествили эти две вершины. В данном случае это не повлияло на язык, распознаваемый источником G1, зато уменьшило число вершин и дуг.
Источник G2 для распознавания итерации с* получим из простейшего двухполюсника, |
|
|
|
|
распознающего слово с, т.е. дуги [и1, и2], помеченной символом с. Для этого согласно |
|
|
|
|
описанным выше правилам добавим две вершины s и t и четыре пустые дуги [s, и1], [и2, и1], |
s |
u1 |
u2 |
t |
[s, t] и [и2, t]. |
|
c |
||
|
|
|
||
Теперь осталось лишь параллельно соединить двухполюсники G1 и G2. В соответствии с |
|
|
|
|
|
|
|
|
правилами параллельного соединения источников для этого следовало бы добавить новую
начальную вершину u и новую заключительную вершину v, а также провести четыре дополнительные дуги, помеченные символом Λ. Однако с целью упрощения источника мы просто отождествим вершину v1 источника G1 с вершиной s
источника G2, а вершину v2 |
с вершиной t. В данном примере это не приведет к изменению распознаваемого языка. Таким |
|||||||
образом, окончательно получаем искомый двухполюсный источник G, распознающий заданное регулярное выражение. |
||||||||
|
|
v2 |
|
Поскольку всякое регулярное выражение представимо в виде суммы, произведения и |
||||
|
|
|
|
|||||
|
а |
b |
|
итерации элементарных языков, то для распознавания любого регулярного языка можно |
||||
|
u1 |
u2 |
|
построить источник |
с помощью |
последовательного и |
параллельного соединений более |
|
s |
t |
простых источников. |
После этого |
для решения задачи |
синтеза достаточно полученный |
|||
|
c |
|||||||
|
|
|
|
|
|
|
||
30
