З

А в

атруднения, возникающие при анализе отношений между этими понятиями, были уже предметом нашего обсуждения. Снять эти затруднения удается, если понимать противоположные понятия, как соподчиненные, а они именно таковы. При таком подходе они полностью укладываются по своим объемным характеристикам в 13-ю схему.

Пятнадцать модельных схем не отражают всей полноты отношений между понятиями. Если понятия являются сложными и их объемы одновременно находятся в различных отношениях, то выявить богатство отношений между ними требуют иного подхода. Различные части объемов сложных понятий могут находиться в самых разнообразных отношениях друг с другом и в этом смысле требуют построения не одной, а многих схем для выявления этих отношений. Более предпочтительным для таких понятий является способ построения диаграмм, знание о котором требует предварительного знакомства с алгеброй Буля.

Диаграммы Венна как прием анализа отношений между понятиями.

Способ представления объемов понятий на кругах Эйлера оказался малопригодным в тех случаях, когда не ясен объем понятия. В частности, если понятие является не простым, а сложным, то возникают неопределенности. Английский логик Джон Венн (1834 - 1923) {главный труд ”Символическая логика” (1991), заметим, что термин “символическая” был применен к логике здесь впервые} разработал графический аппарат диаграмм, с помощью которого выявляются отношения между объемами практически любых понятий. Алгебра Буля здесь получила дальнейшую оригинальную разработку, логика классов стала эквивалентом исчисления первопорядковой логики предикатов.

Например, имеется такое понятие: x ( P(x) & (ךQ(x) V R (x))). Пусть это понятие пробегает по универсумуU. Рассмотрим три способа разделения плоскости универсума на фигуры. Рисуем квадрат (круг), символизирующий этот универсум.

Далее разбиваем его плоскость на 2ⁿпрямоугольников, гдеn– число предикаторов, заданных в анализируемом понятии. В приведенном понятии есть три предикатораP,QиR. Разделим имеющийся универсум по каждому предикатору пополам в такой последовательности: вертикальной чертой для первого предикатора (справа рисуем известные нам круговые схемы и их графические аналоги из логики классов).

Одна его часть (P)означает принадлежность свойстваPпредметам“x”. Другая его часть(ךP) означает: “Неверно, что предметы “x” данного универсума обладают свойствомP”. Обратим внимание на то, что приемом разбиения плоскости надвое осуществляется дополнение одного класса до универсума.

Горизонтальной чертой выделим плоскости для второго предикатора.

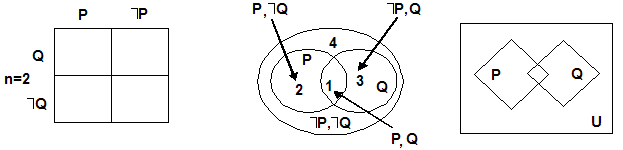
Для третьего предикатора вновь используем вертикальную черту дважды для разбиения плоскостей PиךP. Приn = 3универсум разбивается на 8 областей.

В круговой схеме плоскости означают: 1 – P Q R, 2 – P Q ךR, 3 – ךP Q R, 4 – P ךQ ךR, 5 – ךP Q R, 6 – ךP Q ךR, 7 – ךP ךQ R и 8 – ךP ךQ ךR. Графическая схема имеет соответствующие 8 областей.

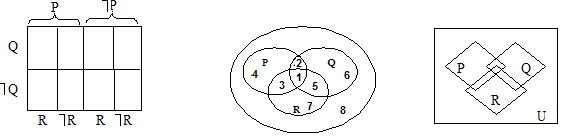
Если бы имелся четвертый предикатор, например S, то плоскостиQиךQделились бы еще горизонтальными чертами с тем, чтобы получить плоскости дляSиךS.

Для четырех предикаторов получили 16 малых квадратов, то есть перебор всех их возможных комбинаций. Черта, разбивающая квадрат, не принадлежит ни к одному из получившихся прямоугольников символизирующих объем какого-либо из предикаторов. Исходной позицией диаграммы в графическом изображении служит взаимное пересечение классов. Каждый прямоугольник диаграммы нумеруется. Приn = 4возможны такие варианты изображения в круговых схемах и графической схемы для логики классов:

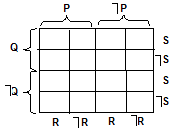
8	4	12	16
6	2	10	14
5	1	9	13
7	3	11	15

U

15 D

C 14 13

11 B

12

6. 9

A 5

1 10

8

7 2

3

4

16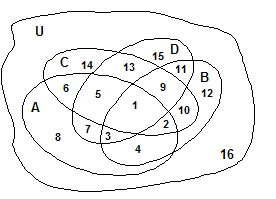

Операции осуществляются следующим образом. Отрицанию соответствует дополнение(‘ ), дизъюнкции соответствует объединение(U), а конъюнкции - пересечение(∩). КаждомуxA(x)будет соответствовать свой объем. Теперь на схеме слева штриховкой устанавливаем объем для первого предикатора(P). На средней схеме штрихуем объем для части понятия(ךQ(x) V R(x))и, наконец, на схеме справа по совместному списку предикаторов находим объем исходного понятияx(P(x) & (ךQ(x) V R(x))).

W_x P(x)

Приведем пример: “Город, такой, что он крупный и, если он имеет пристань, то стоит на реке”.

x(крупный (x) и (еслиxимеет пристань, тоxстоит на реке)). Заменим имеющиеся связи на логические союзы. Будем иметь:

x(крупный (x) & (имеет пристань(x)стоит на реке (x))):

Теперь запишем термины данного выражения символами языка логики предикатов и заменим импликацию на дизъюнкция. После такой процедуры получим знакомую формулу: