Министерство образования Российской Федерации

Новосибирский государственный технический университет

________________________________________________________

МЕХАНИКА

И ТЕРМОДИНАМИКА

Лабораторный практикум по физике для студентов

1, 2 Курсов всех факультетов и форм обучения

Новосибирск

2003

Составители: В.Г. Дубровский, А.А. Корнилович,

И.И. Суханов, А.А. Харьков

Рецензент В.Н. Холявко

Работа подготовлена на кафедре прикладной

и теоретической физики

Новосибирский государственный

технический университет, 2003

Вводное занятие

1. Основные понятия теории измерений

Целью измерений является получение количественной информации об измеряемой физической величине, ее истинном значении . Измеренное значение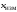из-за множества причин может не совпадать с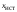. Следовательно, результаты измерений дают нам не точное значение, а лишь его оценку.

Меры погрешности. Абсолютная погрешность – это отклонение измеренного значения от истинного: . В единичном измерении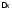может иметь произвольный знак.Относительная погрешность – это отношение абсолютной погрешности к измеряемой величине

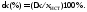или (1)

2. Лабораторная установка

В лабораторной работе измеряется время соударения двух металлических шаров, подвешенных на проводящих нитях (рис. 1). Измерительная установка состоит из электромагнита ЭМ, микросекундомера МС и источника напряжения. Установка включается тумблером «ВКЛ». Нажатием кнопки «СТОП» включается ток через обмотку ЭМ. Шар 1 отводится в сторону до соприкосновения с ЭМ. Необходимо нажать кнопку «СБРОС», чтобы индикатор МС показывал нулевое значение. При нажатии кнопки «ПУСК» прерывается ток через обмотку ЭМ, шар 1 ударяется о свободно висяший шар 2, замыкается электрическая цепь через шары. Время существования тока в этой цепи, считающееся временем соударения шаров, измеряется МС и показывается на его индикаторе.

Результаты многократных измерений и последующих расчетов удобно представить в виде табл. 1. Здесь k – порядковый номер измерения, x_k – измеренное время соударения.

Таблица 1

Таблица измерений

k	xk мкс		Интервалы	n	n / n	, мкс
1	x1		xmin + b	4	0,08	–
2	x2		xmin + 2b	10	0,2	s, мкс
.	.		…	…	…	…
.	.		…	…	…	ПШПВ, мкс
.	.		xmax	2	0,04	–
n		xn

Примечание. ПШПВ – полуширина на полувысоте.

3. Математическая обработка результатов измерений

Гистограмма. Предположим, произведено n измерений времени соударения шаров x. Среди измеренных значений есть x_min и x_mах. Пусть, например, x_min = 106 мкс, x_min = 118 мкс. Разобьем диапазон x_mах – x_min на r 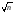интервалов. Приn = 50 возможные значения r = 6, 7 или 8. Выберем r = 6, тогда ширина одного интервала b = (x_max – x_min) / r = (118 – 106) / 6 = 2 мкс. В столбце «Интервалы» табл. 1 запишем правые границы интервалов: x_min + b, x_min + 2b, …, x_max . Подсчитаем число измерений n, попавших в каждый из интервалов. Результат измерения, попавший точно на границу между интервалами, следует относить всегда либо к левому, либо к правому интервалу. Пусть, например, в первый интервал, между x_min и x_min + b попали четыре измерения, во второй – 10 и т. д. Необходимо проверить, что сумма всех n равна полному числу измерений n. Подсчитаем относительную частоту n/n для каждого интервала и запишем ее в столбец таблицы. Очевидно, что сумма всех частот равна единице. Строим гистограмму в осях n/n и x (рис. 2). Над каждым интервалом строим прямоугольник высотой n/n и шириной b. Гистограмма – ступенчатый график относительной частоты – наглядно показывает распределение результатов измерений.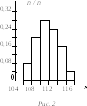

Теоретическая плотность вероятности. Если все ординаты на рис. 2 разделить на b, изменится только вертикальный масштаб гистограммы. Эта преобразованная гистограмма при n и b dx 0 перейдет в плавную кривую p(x), показанную на рис. 3. Функция p(x) = (dn/n) / dx называется дифференциальной функцией распределения или плотностью вероятности. Вероятность попадания результата измерения dP(x, x + dx) в интервал от x до x + dx, т. е. доля результатов измерений dn/n в этом интервале, при dx 0 равна площади прямоугольника p(x)dx. Естественно, полная вероятность получения любого результата измерения равна единице

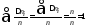или ,

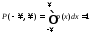т. е. площадь под кривой p(x) равна единице.

Если действуют много независимых причин, каждая из которых слабо влияет на общий результат, то по какому бы закону ни были распределены эти составляющие, суммарный результат распределен по нормальному закону Гаусса:

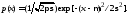(2)

Свойства нормального распределения (рис. 3):

1) существует наиболее вероятное значение x(p = max) = ;

2) отклонения x от в обе стороны встречаются одинаково часто: гауссово распределение симметрично относительно , поэтому среднее значение 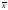, называемое также математическим ожиданием величиныx, равно ;

3) чем больше отклонение x от , тем реже оно встречается;

4) мерой случайной погрешности, т. е. мерой отклонения x от , является «сигма» – стандартное или среднеквадратичное отклонение (СКО), которое примерно равно полуширине на полувысоте гауссова распределения (ПШПВ 1,18 );

5) при 0 все распределение «стягивается» к одному значению x = , которое в отсутствие систематической погрешности и принимается за ;

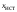6) в интервал вокруг попадает 68 % всех результатов измерений, в интервал 2 – 95 %, а в интервале 3 заключено 99,73 % всех результатов. На долю отклонений от , превышающих 3, приходится всего 0,27 %, что меньше 1/300 общего числа измерений. Таким образом, с вероятностью P интервал между и результатом любого измерения x_k равен:

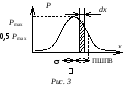
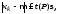, (3)

P 0,68, t = 1; P 0,95, t = 2; P 0,9973, t = 3

Прямые измерения. При прямых измерениях физическая величина считывается непосредственно со шкалы прибора. В данной работе с помощью микросекундомера осуществляется прямое измерение интервала времени, так как перед каждым измерением показание МС сбрасывается в нуль.

Прямое однократное измерение. Возможна оценка по результату однократного измерения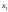, если предварительно на данной измерительной установке проведены многократные измерения (n > 30), в результате чего СКО определено с высокой точностью. Из (3) получаем варианты доверительного интервала для , т. е. интервала, в которомнаходится с заданной доверительной вероятностьюP:

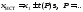(5)

С вероятностью 1 – Р истинное значение может оказаться и вне доверительного интервала (5), поэтому запись интервала обязательно следует сопровождать указанием доверительной вероятности Р .

Допустима форма записи

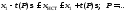(6)

Значения 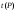, отличные от 1, 2, 3, и соответствующие значенияP могут быть выбраны по таблицам в [1, 2]. Рекомендуется результат записывать для P = 0,95, т.е. выбирать доверительный интервал 2 .

Однократными измерениями, как прямыми, так и косвенными, можно ограничиться во всех лабораторных работах данного практикума (за исключением вводного занятия). Сред-неквадратичные отклонения измеряемых величин указаны на пояснительных табличках к каждой лабораторной работе. Если характеристики погрешности не указаны, то оценка производится по цене деления шкалы 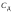. Принято считать, что для шкалы с интервалом между штрихами 1 мм, рассматриваемой с расстояния наилучшего зрения 250 мм, погрешность отсчета равна 0,3…0,5 деления, т. е. в едини­цах измеряемой величины (0,3…0,5).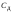

Прямые многократные измерения. Если СКО измеряемой величины неизвестно, то его можно определить многократными, т. е. повторяющимися, измерениями. Этот метод и используется во вводном лабораторном занятии. Расчетной оценкой математического ожидания является выборочное среднее 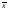, а оценкой – выборочное СКОs:

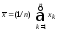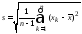, . (7)

Многие из инженерных калькуляторов имеют режим статистических вычислений (STAT), существенно упрощающий вычисления по формулам (7).

При 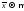, а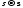. Поэтому, казалось бы, можно по аналогии с (5) записать доверительный интервал

; Р = …

Однако при любом конечном числе измерений выборочное СКО может оказаться как больше, так и меньше неизвестного . Второй случай – самый опасный: при подстановке s вместо преуменьшается ширина доверительного интервала. Заданную доверительную вероятность обеспечивают, расширяя интервал путем замены коэффициентов t(P) на коэффициенты Стьюдента (табл. 2) t(P, n) > t(P). Из таблицы видно, что, например, t(P =0,95; n) t(P) только при n 30, т. е. только при таком числе измерений s незначительно отличается от . С другой стороны, для сужения интервала, т. е. для уточнения оценки , используют то обстоятельство, что выборочное среднее 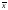в (7) зависит от суммы случайных нормально распределенных результатов измерений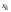и потому само является случайной нормально распределенной величиной со среднеквадратичным отклонением сред-него:

, ,.

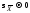Это означает, что, хотя от измерения к измерению единичные результаты «прыгают» в среднем на , разброс выборочных средних от выборки к выборке по n случайных измерений уменьшается с ростом n, что и позволяет сузить доверительный интервал, проводя многократные измерения. Уменьшение случайного разброса путем усреднения многократных измерений широко используется в цифровых приборах.

Таблица 2
n	Р
	0,9	0,95		0,99	0,997
	t(P, n)
2	6,3	12,7	63,6		212,3
3	2,9	4,3	9,9		182
4	2,4	3,2	5,8		9,0
5	2,1	2,8	4,6		6,4
б	2,0	2,6	4,0		5,4
7	1,9	2,4	3,7		4,8
8	1,9	2,4	3,5		4,4
9	1,9	2,3	3,4		4,2
10	1,8	2,3	3,2		4,0
15	1,8	2,1	3,0		3,6
20	1,7	2,1	2,9		3,4
30	1,7	2,0	2,8		3,2
50	1,7	2,0	2,7		3,1

Используя коэффициенты Стьюдента и переходя к выборочному СКО среднего значения, окончательно запишем доверительный интервал для результата многократных измерений

(8)

Косвенные измерения. При косвенных измерениях физическая величина вычисляется по формуле через величины, полученные в прямых измерениях. Даже простые линейные измерения являются, вообще говоря, косвенными, так как измеряемый размер L вычисляется из двух координат (начальной 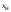и конечной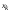) по формуле.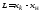

Если физическая величина y вычисляется по формуле через нормально распределенные величиныa, b, c, … , с СКО , полученные в прямых измерениях, тоy также распределена нормально с СКО:

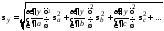(9)

Однократное косвенное измерение. Пусть измерены значения 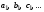величинa, b, c, … . Тогда доверительный интервал равен

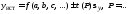(10)

Значения P и t(P) см. в (3), а 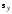вычисляется по (9).