5.5. Ток смещения

Как уже отмечалось в разд. 5.1, изменяющееся магнитное поле порождает вихревое электрическое поле.

Максвелл предположил, что должно существовать и обратное явление – изменение электрического поля должно порождать магнитное поле.

Поэтому он поставил перед собой задачу – доказать, что изменяющееся электрическое поле порождает магнитное поле и объяснить механизм этого явления.

Рассмотрим решение этой задачи (проведённый далее анализ существенно упрощен, но полученные выводы будут пра-вильными).

Пусть имеется конденсатор, который заряжается от источника эдс.

Пока происходит заряд, в проводниках, соединяющих обкладки конденсатора с источником эдс, идёт ток прово-димости. Кроме этого, в процессе зарядки изменяется заряд на обкладках конденсатора и растёт напряжённость электрического поля между обкладками.

В разд. 1.22 показано, что напряжённость Е электрического поля внутри конденсатора равна (здесь – поверхност-ная плотность заряда на обкладках конденсатора,  – диэлектри-ческая проницаемость вещества между обкладками конден-сатора).

Из последнего выражения следует, что

_оЕ = .

В разд. 1.17 показано, что

_оЕ = D,

т. е. произведение напряжённости электрического поля на электрическую постоянную и диэлектрическую проницаемость диэлектрика равно вектору электрического смещения. Это выражение можно переписать в скалярной форме: _оЕ = D.

Но это означает, что  = D, т. е. поверхностная плотность заряда на обкладках конденсатора равна модулю вектора электрического смещения.

Продифференцируем последнее выражение по времени

(использование частных производных обусловлено тем, что поверхностная плотность заряда может зависеть не только от времени, но и от координаты).

Производная от поверхностной плотности заряда по времени есть плотность тока проводимости j_пр =

Но тогда и правая часть равенства имеет размерность плотности тока.

Здесь следует обратить внимание на важную деталь.

В левой части равенства присутствует поверхностная плотность заряда , изменение которой обусловлено упорядоченным движением свободных носителей заряда в проводниках, соединяющих обкладки конденсатора с источником эдс. Поэтому можно сказать, что левая часть равенства относится к той части цепи, в которой может протекать ток проводимости.

В правой части равенства присутствует модуль вектора электрического смещения, который является характеристикой электрического поля в диэлектрике. Следовательно, правая часть равенства относится к той части цепи, где отсутствуют свободные носители заряда и где токи проводимости протекать не могут.

Тем не менее имеет размерность плотности тока.

Поэтому Максвелл предположил, что в диэлектрике может существовать особый ток, природа которого существенно отлич-на от природы тока проводимости. Он назвал этот ток током смещения.

По определению, плотность тока смещения

.

Как отмечено выше, , поэтому

j_пр = j_см,

т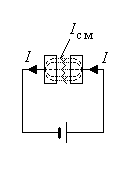. е. плотности тока проводимости и тока смещения в замкнутой цепи всегда равны. Таким образом, ток непрерывен не только в цепях, состоящих из проводников, но и в цепях, содержащих непроводящие элементы (например, конденсаторы).

Рассмотрим природу тока смещения.

Производная, расположенная в правой части равенства, может быть записана следующим образом:

(здесь использовано определение вектора электрического смещения, данное в разд. 1.17).

Следовательно, j_см = , или в векторной форме

.

Рассмотрим этот ток подробнее.

Слагаемое (производная от поляризованности по време-ни) связано с процессами, протекающими в ходе поляризации диэлектрика.

Как отмечено в разд. 1.15, в полярных диэлектриках происходит поворот атомов так, чтобы их дипольный момент стал параллелен силовым линиям электрического поля.

В неполярных диэлектриках происходит смещение* элект-ронных оболочек атомов в одну сторону, а ядер – в противо-положную.

_____________________________

* Отсюда и происходит название тока смещения.

Поэтому можно сказать, что является плотностью тока, возникающего из-за упорядоченного движения атомов диэлектрика в процессе его поляризации.

Слагаемое не равно нулю, если с течением времени изменяется напряжённость электрического поля.

Но электрическое поле может изменяться и там, где нет носителей заряда (например, в вакууме).

Следовательно, эта компонента тока смещения не связана с какими-либо зарядами. Она порождается изменяющимся электри-ческим полем.

Ток проводимости в проводниках создаёт магнитное поле.

Но тогда и ток смещения должен создавать такое же магнитное поле (так как j_пр = j_см).

Экспериментальная проверка показала, что это предполо-жение верно. Между обкладками конденсатора существует точнотакое же магнитное поле, как и вокруг проводников, соединённых с обкладками.

Так была подтверждена правильность гипотезы Максвелла о существовании тока смещения и доказано, что токи смещения наряду с токами проводимости являются источником магнит-ного поля.

Е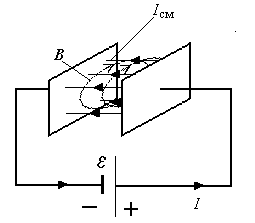щё раз обратите внимание на очень важную деталь:ток смеще-ния может существовать в среде, не содержащей заряженных час-тиц (в вакууме). Если в такой среде имеется изменяющееся во времени электрическое поле, то в ней суще-ствует и ток смещения.

Кроме тока смещения, Максвелл ввёл понятие полного тока. Полный ток – это ток, равный сумме тока проводимости и тока смещения.

Плотность полного тока

.

В свою очередь, сила полного тока равна

.