Смещение аргумента

. (1.9)

Сдвиг аргумента функции приводит к сдвигу фазы фурье-образа

Доказательство

Записываем левую сторону (1.9) в явном виде, используя (1.1):

.

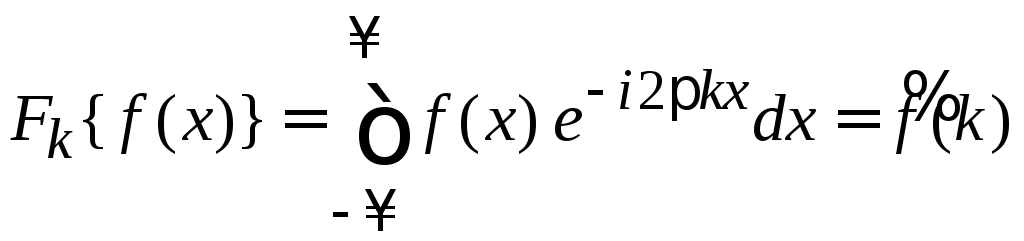Заменяем аргумент так, чтобы интеграл вернулся к стандартному виду (1.1). Результат сравниваем с (1.1):

.

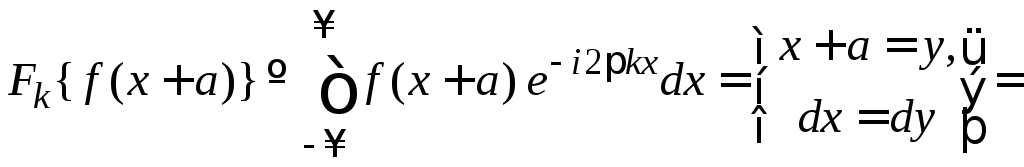
Фазовый сдвиг

. (1.10)

Сдвиг фазы функции приводит к сдвигу аргумента фурье-образа

Доказательство

Из (1.1) получаем

.

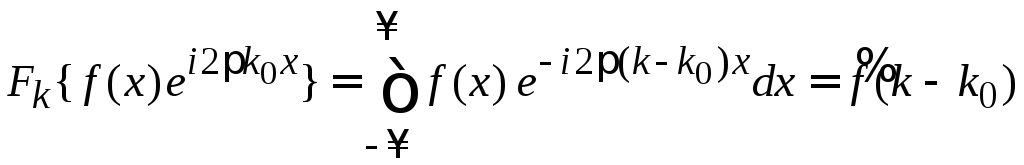Комплексное сопряжение

. (1.11)

Комплексное сопряжение функции приводит к комплексному сопряжению фурье-образа и инверсии его аргумента.

Доказательство

В (1.1)

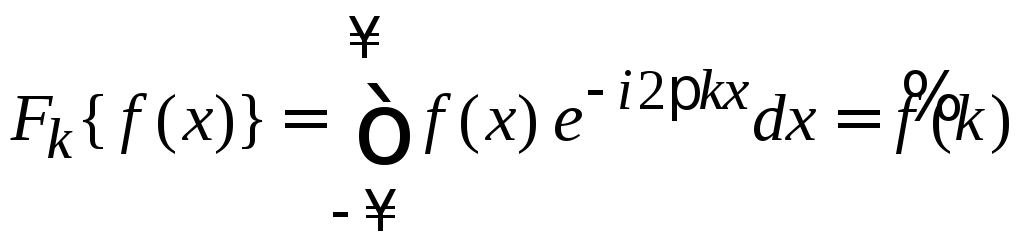
подставляем

.

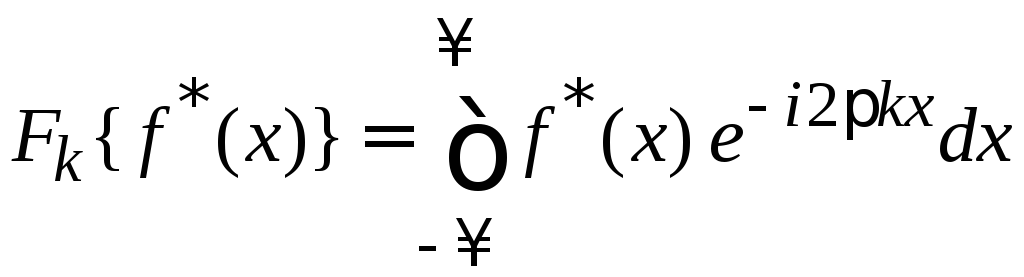Выполняем комплексное сопряжение (1.1)

.

Сравнение интегралов дает (1.11).

Следствия (1.7) и (1.11)

,

.

1) Если – вещественная и четная, то – вещественная и четная.

Доказательство

Используем

,

.

Левые стороны равны по условию задачи, следовательно:

и фурье-образ вещественный.

Доказать самостоятельно:

2) Если – вещественная и нечетная, то – мнимая и нечетная;

3) Если – мнимая и четная, то – мнимая и четная;

4) Если – мнимая и нечетная, то – вещественная и нечетная.

Теорема Парсеваля

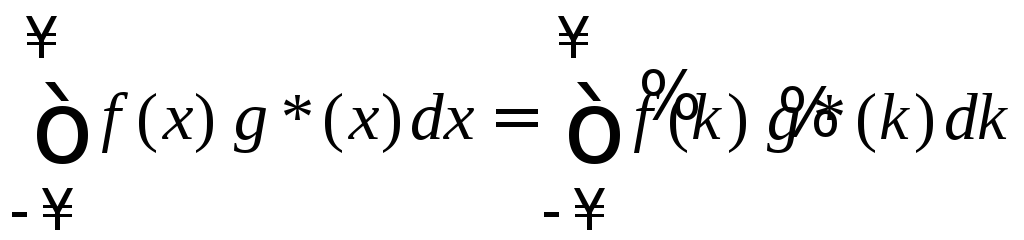. (1.14)

Левая сторона (1.14) соответствует определению (0.5) скалярного произведения функций и, тогда (1.14) означает сохранение скалярного произведения функций при преобразовании Фурье. Применительно к физике теорема выражает, в частности, закон сохранения энергии и вероятности при преобразовании Фурье.

Марк-Антуан Парсеваль (1755–1836) – французский математик. Исследовал дифференциальные уравнения и функции комплексного переменного. Теорему доказал в 1799 г.

Доказательство

Используем (1.1) и (1.2)

,

,

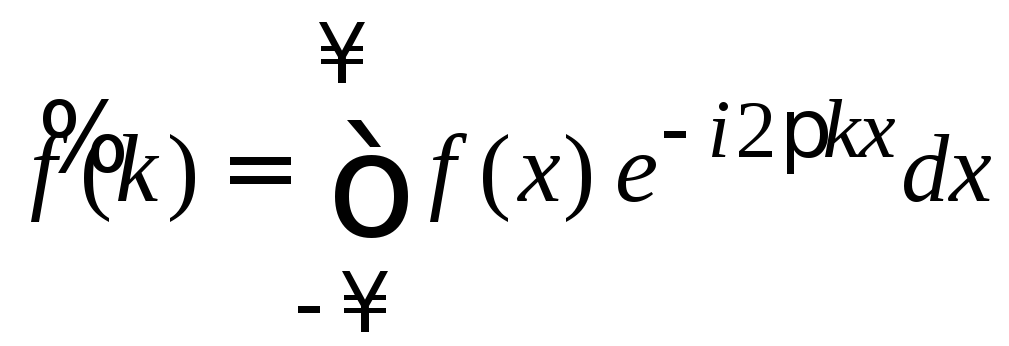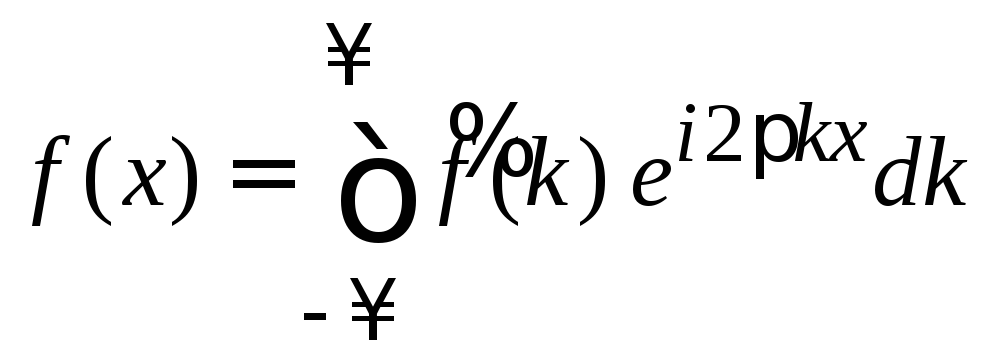тогда

.

Считаем интегралы существующими, и получаем

=,

где изменен порядок интегрирований.

Обобщенная теорема Парсеваля

. (1.15)

При иполучаем (1.14).

Ортонормированность базиса и его фурье-образа

Если функции и взаимно ортогональны

,

то их фурье-образы также ортогональны

.

Теорема доказывается подстановкой ив (1.14). Выполняется и более общее утверждение

Если функции и ортонормированные

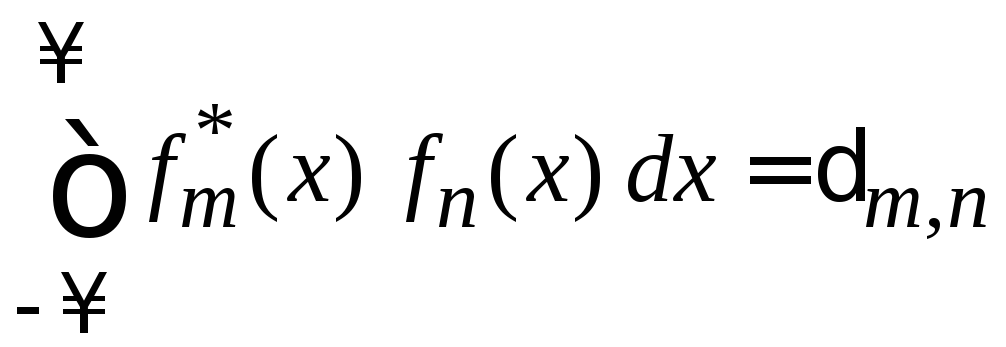, (1.16)

то их фурье-образы также ортонормированные

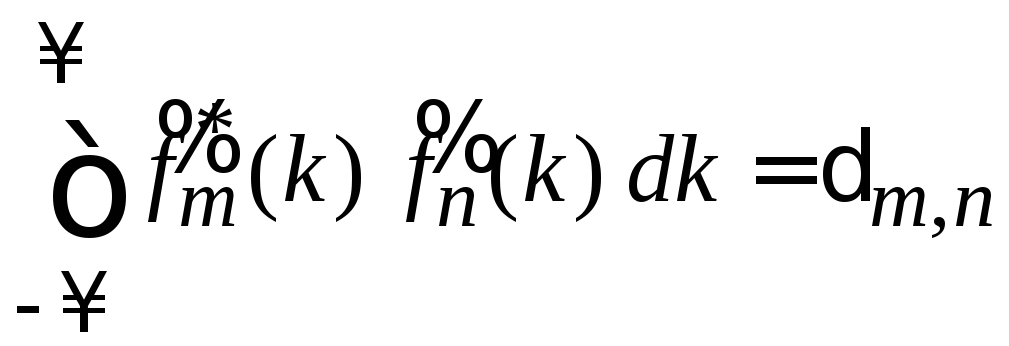. (1.17)

Доказательство

В (1.14)

полагаем и.

Интегральная теорема

Прямое и обратное преобразования Фурье восстанавливают непрерывную функцию

,

. (1.20)

Доказательство

Используем (1.1) и (1.2)

,

.

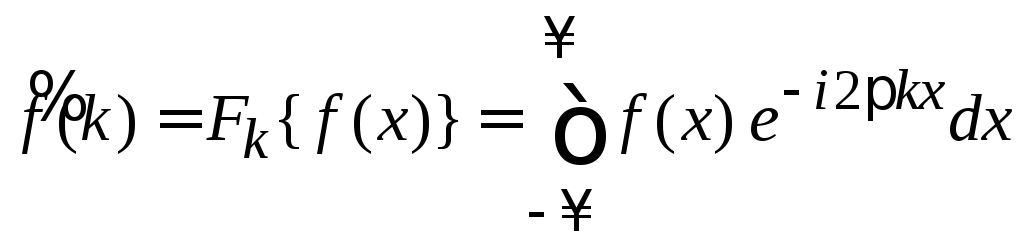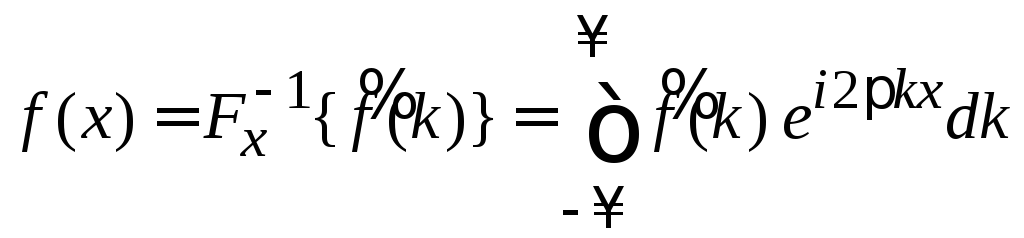Подставляем (1.2) в (1.1)

,

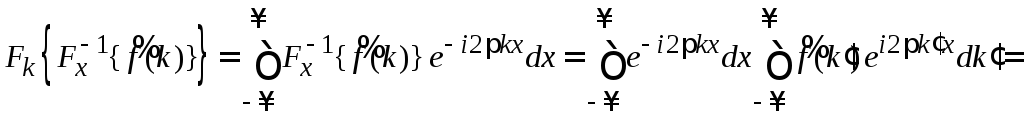
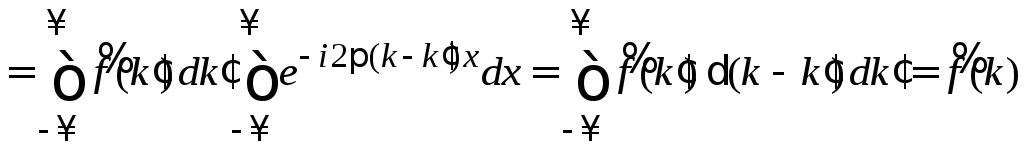где заменен порядок интегрирований и использованы свойства дельта-функции

,

.

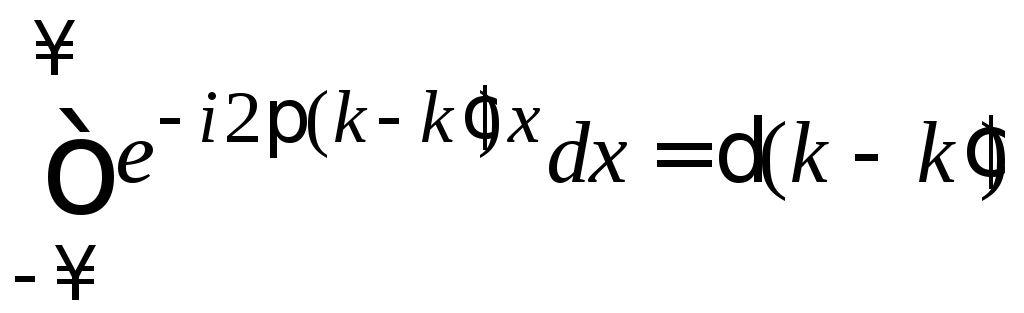Следовательно, для непрерывной функции операторами тождественного преобразования являются:

, . (1.20а)

Если функция в точкеимеет разрыв

,

тогда оператор в точкеусредняет функцию

.

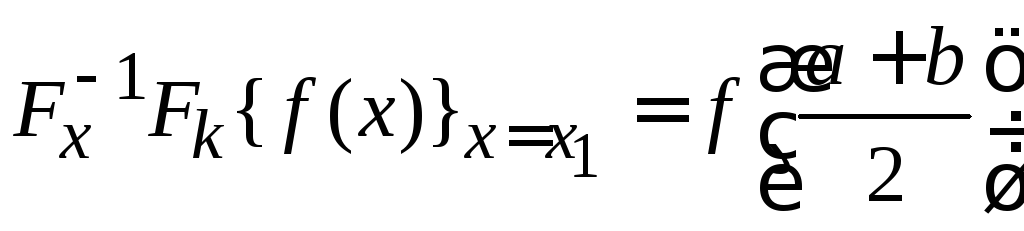Теорема о парах функций

Функция и ее фурье-образназываются «парой функций». Если

,

то выполняется

. (1.21)

Доказательство

Используем (1.1), заменяем аргумент , полученный интеграл сравниваем с интегралом в (1.2)

.

, (1.1)

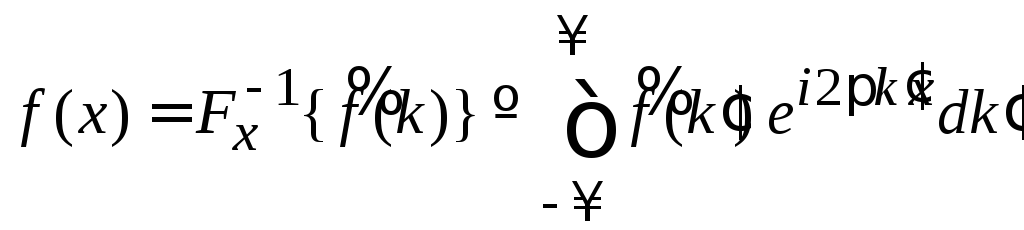. (1.2)