Необходимые базовые знания

Векторная алгебра.

Комплексные числа.

Основы математического анализа.

Основы общей физики.

Литература

1. Файлы лекций.

2. Учебное пособие для практических занятий и лекций:

Краснопевцев Е.А. Математические методы физики. 53

Ортонормированные базисы функций. Изд. НГТУ, 2008. К 782

Дополнительная литература

1. Приведена в конце учебного пособия.

2. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся ВУЗов.

ОРТОНОРМИРОВАННЫЕ БАЗИСЫ

В ВекторнОМ пространствЕ

Базис – система координат, образованная единичными взаимно перпендикулярными векторами – ортами. Ортогональные координаты применяются во всех разделах физики и техники. В результате:

упрощается решение задачи;

результаты выражаются через проекции – числа;

решение становится наглядным.

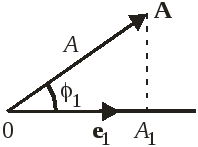
Вектор A – направленный отрезок, обозначается жирной, прямой буквой.

–модуль, или норма вектора, число, обозначается буквой курсивом;

–орт (от греч. ορθός – прямой), единичный вектор , перпендикулярный всем остальным ортам базиса;

–проекция вектора на направление орта , число,равное скалярному произведению вектора на орт

,

где –знак тождества, является определением величины, т. е. равенством, которое выполняется при любых условиях.

Если угол , тоивектора ортогональны, то есть перпендикулярны .

Норма вектора

.

Вектор нормирован, если .

Декартова система координат введена Декартом в 1637 г.

Рене Декарт (1596–1650)

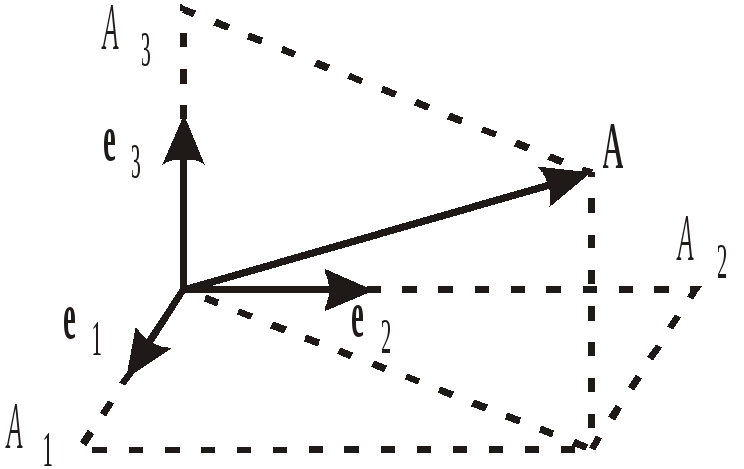
Базис в трехмерном пространстве – совокупность ортов ;

–проекции вектора на орты,;

–составляющая вектора ;

–вектор равен векторной сумме своих составляющих.

ВекторнОе пространствО

Векторное пространство – множество векторов, для которых определено скалярное произведение.

Размерность пространства равна числу независимых ортов, через сумму которых выражается произвольный вектор этого пространства.

3-мерное пространство

Базис ортов

Произвольный трехмерный вектор разлагается по трем ортам, образующим базис:

,

, .

Ортонормированность базиса – вектора базиса взаимно перпендикулярны и нормированы

.

Символ Крόнекера

(0.1)

ввел Крóнекер в 1866 г. Выполняется свойство симметрии

,

фильтрующее свойство

.

Леопольд Крóнекер (1823–1891)

N-мерное пространство

Базис

, ,

ортонормированность

. (0.2)

Разложение вектора на составляющие

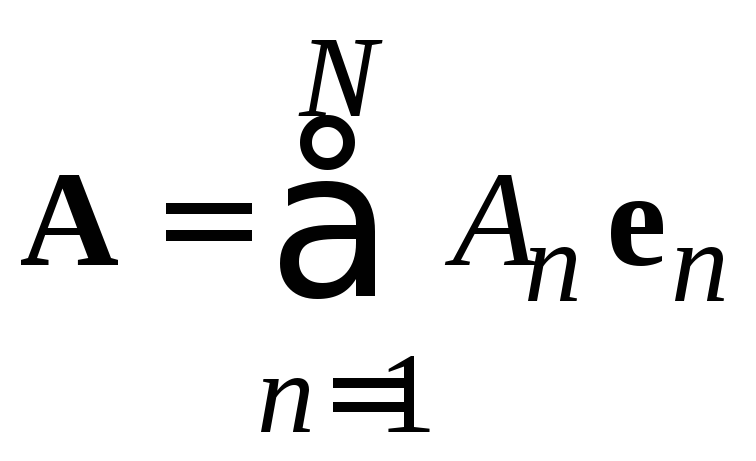. (0.3)

Проекция вектора на орт

. (0.4)

Теорема Пифагора выражает модуль вектора через его проекции

.

Доказывается подстановкой разложения вектора (0.3) в определение модуля и использованием ортонормированности базиса (0.2).

От пространства векторов переходим к пространству функций.

Гильбертово пространство с дискретным базисом

Гильбертово пространство образуется множеством комплексных, квадратично интегрируемых функций, для которых определено скалярное произведение. Введено Гильбертом в 1910 г. Строится аналогично векторному пространству.

Давид Гильберт (1862–1943)

Базис ортов – совокупность функций

, ,

N – размерность пространства – конечное или бесконечное число;

–комплексная, квадратично интегрируемая функция, определенная на интервале вещественного аргумента .

Скалярное произведение является интегралом по области определения функций

, (0.5)

где – вещественнаявесовая функция; – комплексно сопряженная функция.

Комплексное сопряжение является преобразованием, обозначаемым знаком *. Определяем:

вещественная единица ,

мнимая единица ,,

.

Комплексное число a складывается из вещественной части и мнимой части

,

тогда

,

где – модуль числа; φ – фаза числа.

Квадрат модуля числа

,

фаза числа

.

Представление комплексного числа a точкой на плоскости.

Формула Эйлера

Откуда получаем

, ,

,

.

Формулу получил Эйлер в 1740 г.

Леонард Эйлер (1707–1783)

Условие ортонормированности базиса функций

. (0.6)

Разложение функции по базису

, (0.7)

где – множество проекций, илиспектр функции f(x). Проекция функции на орт

. (0.8)

Подстановка (0.8)→(0.7) дает тождество

,

если базис полон.

Условие полноты базиса

, (0.9)

где –дельта-функция,

Фильтрующее свойство дельта-функции

,

где .

Теорема Парсеваля – является аналогом теоремы Пифагора в пространстве функций – квадрат модуля вектора равен сумме квадратов его проекций

, (0.10)

где

, .

Предполагается, что интеграл и сумма в (0.10) существуют. Теорему получил Мари-Антуан Парсеваль в 1799 г.

Доказательство

Подставляем (0.7)

в левую сторону (0.10)

.

Меняем порядок суммирований и интегрирования, считая суммы конечными. Вычисляем интеграл, используя ортонормированность базиса (06):

.

Фильтрующее свойство символа Кронекера снимает одну сумму

,

получаем теорему Парсеваля

.