Оптическое преобразование Фурье

Анализатор частот функции, Анализатор волновых чисел

зависящей от времени – функции, зависящей от координат

спектрометр

На призму с дисперсией падает Плоская волна падает

волна с зависимостью на транспарант с

от времени . коэффициентом пропускания.

Призма преобразует: Линза преобразует:

время → частота, координата → волновое число,

, ,

амплитуда распределена амплитудараспределена

по углам. вдоль линии в фокальной плоскости.

, ,

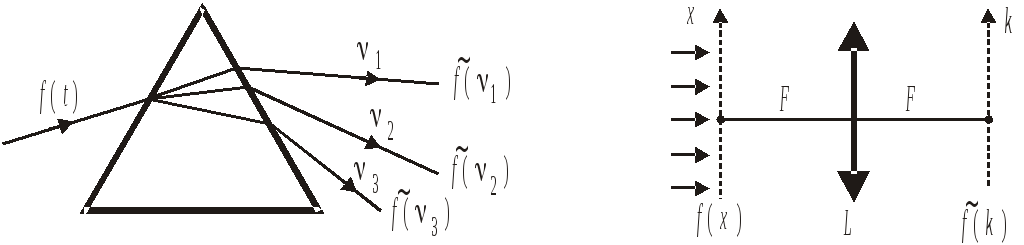
Теоремы Фурье Линейность преобразования

. (1.5)

Линейное преобразование функции приводит к аналогичному преобразованию Фурье-образа. Результат следует из линейности операции интегрирования в (1.1)

.

Масштабное преобразование аргумента функции. Если

,

то

. (1.6)

Сжатие функции приводит к расширению фурье-образа, и наоборот. При функция сжимается вдоль осиx, при этом ее фурье-образ расширяется вдоль оси k и уменьшается его величина в a раз.

Доказательство

Записываем левую сторону (1.6) в явном виде, используя (1.1):

.

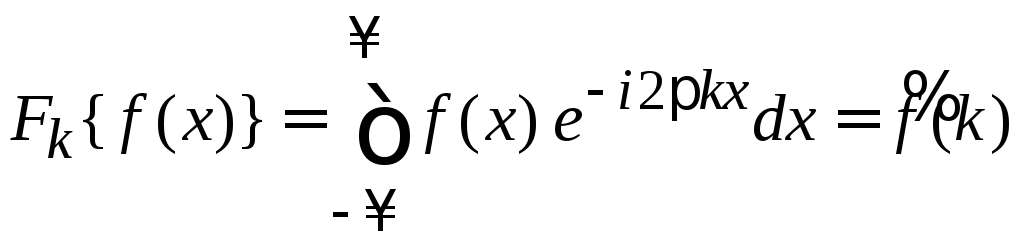Заменяем аргумент так, чтобы интеграл вернулся к стандартному виду (1.1). Результат сравниваем с (1.1)

.

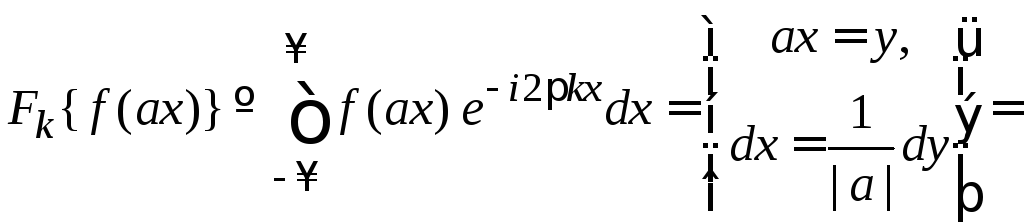
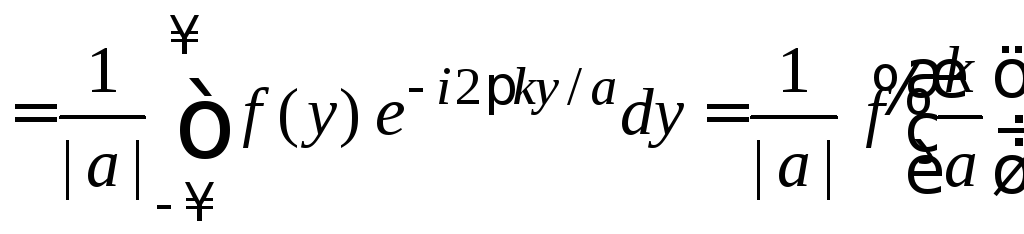Пример: Функция Гаусса

, .

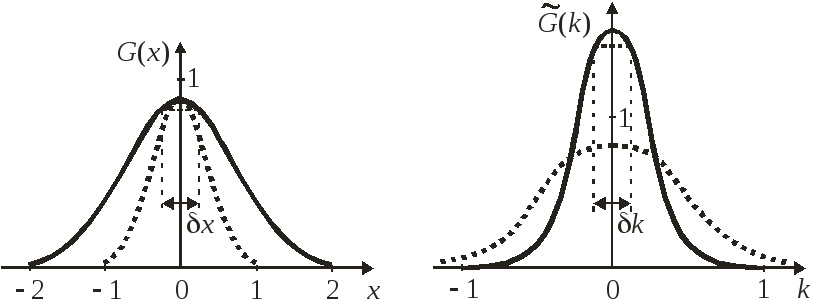
При масштабном преобразовании с происходит сжатие по x в 2 раза, что соответствует переходу от сплошной линии к пунктирной. Фурье-образ растягивается по k, амплитуда уменьшается в 2 раза.

Инверсия аргумента

Из (1.6)

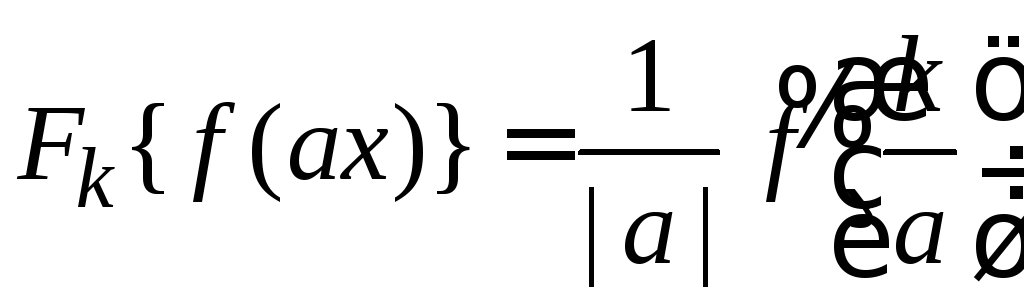
при получаем

. (1.7)

Четности функции и ее фурье-образа совпадают. Если – четная функция, то и– четная функция; если– нечетная функция, то и– нечетная функция.

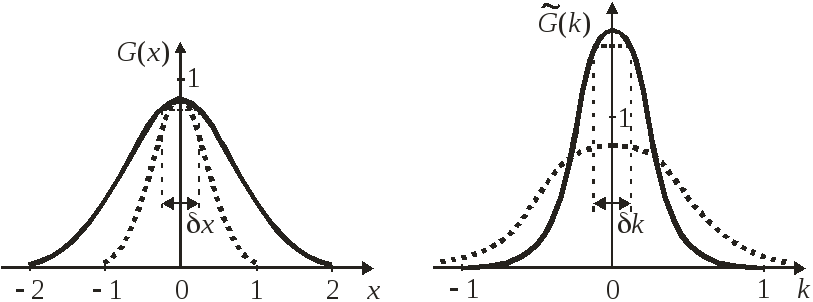
Теорема о частотной полосе

Флуктуации фурье-сопряженных величин связаны соотношением

, (1.8)

где дисперсия – среднее квадратичное отклонение определяется в виде

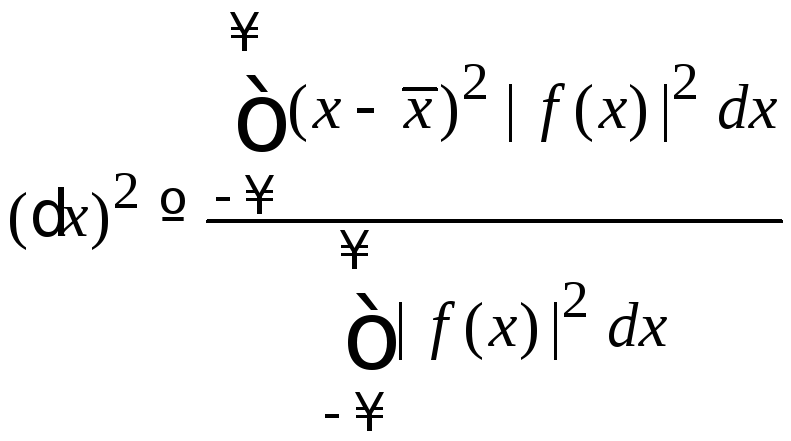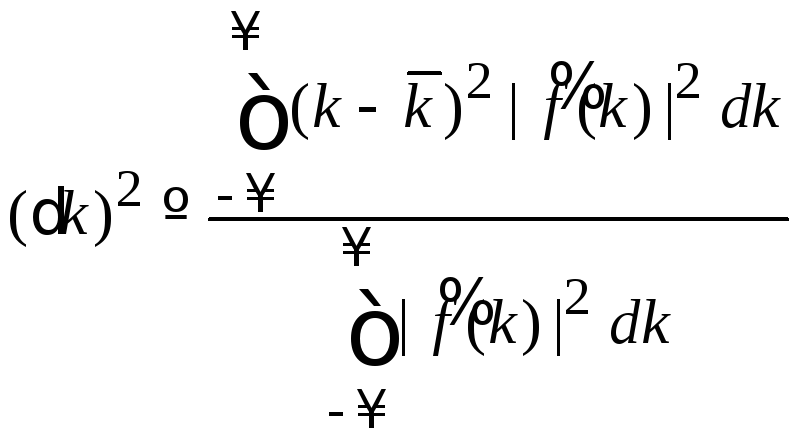; . (1.8,а)

Уменьшение пространственной протяженности функции приводит к увеличению частотной протяженности ее образа, и наоборот, как показано на рисунке.

Для функции Гаусса

,

,

из (1.8,а) следует

, ,

выполняется

.

Следствием теоремы (1.8) применительно к дифракции рентгеновского излучения на тонком образце, содержащем множество нанокристаллов, является формула Дебая – Шеррера

,

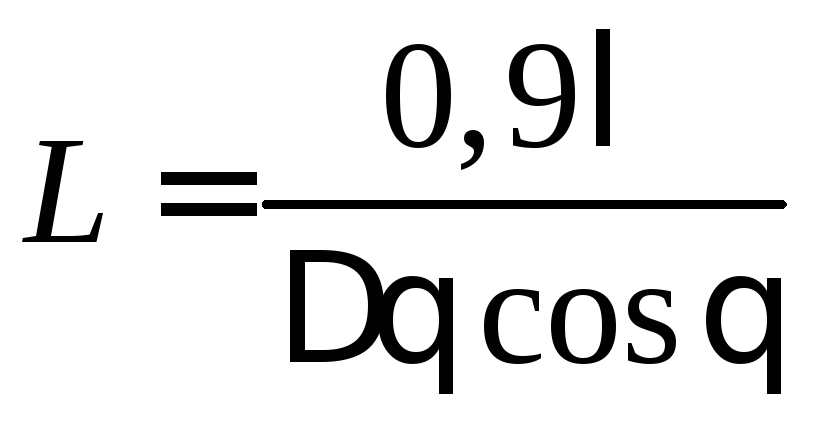используемая для измерения размера нанокристалла. Параллельный пучок излучение с длиной волны λ после дифракции на образце становится расходящимся в угловой интервал .Ширина дифракционной кривой обратно пропорциональна размеру нанокристалла. Чем меньше размер L нанокристалла, тем больше угловая расходимость дифрагированного пучка.