
- •Методы математической физики
- •Краснопевцев Евгений Александрович
- •Ортонормированные базисы функций
- •Рейтинговая аттестация по дисциплине с экзаменом
- •Рейтинговая аттестация по дисциплине с зачетом
- •Необходимые базовые знания
- •ВекторнОе пространствО
- •Гильбертово пространство с дискретным базисом
- •Гильбертово пространство с непрерывным базисом
- •Преобразование фурье
- •Оптическое преобразование Фурье
- •Теоремы Фурье Линейность преобразования
- •Инверсия аргумента
- •Теорема о частотной полосе
- •Смещение аргумента
- •Фазовый сдвиг
- •Комплексное сопряжение
- •Теорема Парсеваля
- •Обобщенная теорема Парсеваля
- •Ортонормированность базиса и его фурье-образа
- •Интегральная теорема
- •Теорема о парах функций
- •Свертка функций
- •Теорема о свертке
- •Разложение в ряд Фурье комплексной периодической функции
- •Фурье-образ периодической функции
- •Теорема о дифференцировании
- •Разложение в ряд Фурье вещественной периодической функции
Свертка функций
Операция свертки двух функций является интегральным преобразованием и обозначается звездочкой, которая ставится между функциями:
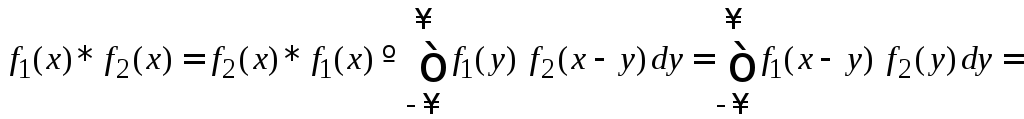
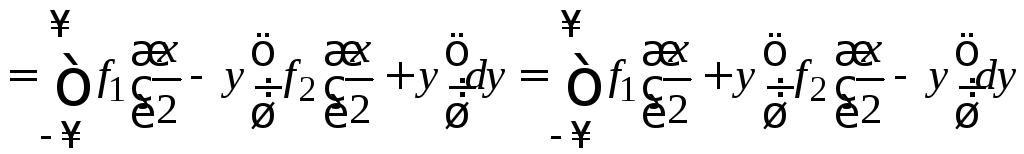 .
(1.22)
.
(1.22)
Равенства
в (1.22) получены заменами аргумента
![]() в виде
в виде
![]()
с параметрами
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
При
замене
![]() использовано
использовано
 .
.
Особенность форм в (1.22) – сумма аргументов у двух функций под интегралом равна x.
Свертка с постоянной
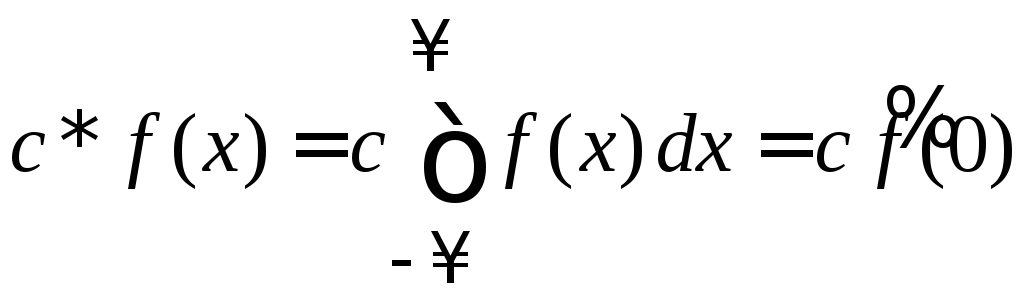 ,
,
![]() .
.
Физический смысл свертки. Рассмотрим преобразователь сигналов
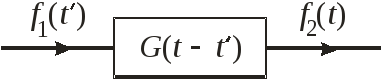
f1(t') – входящий сигнал (например, ЭДС) в момент t',
f2(t) – выходящий сигнал (например, ток) в момент t.
Для линейного и стационарного преобразователя сигналов выполняются:
1) принцип суперпозиции – входящие сигналы для разных моментов времени преобразуются независимо, не влияя друг на друга, поэтому преобразование линейное;
2) принцип причинности – если входящий сигнал включается в момент t', то выходящий сигнал отсутствует при более ранних временах t < t';
3) принцип однородности – реакция преобразователя в момент t на сигнал, поступивший в момент t', не изменяется при сдвиге начала отсчета времени, поэтому реакция зависит от (t – t'). Однородность по времени выполняется для стационарного преобразователя с постоянными параметрами.
Этим принципам удовлетворяет свертка
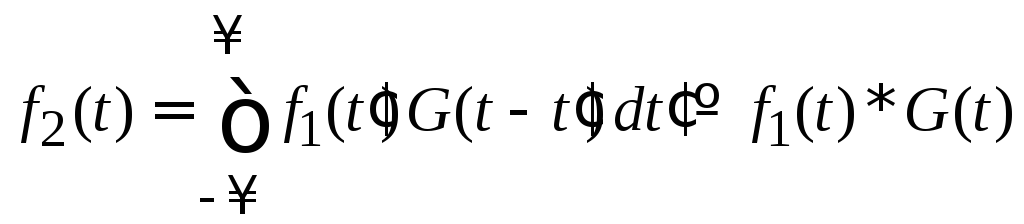 ,
,
где
![]() –функция Грина
– реакция преобразователя
на импульсный
входящий сигнал;
–функция Грина
– реакция преобразователя
на импульсный
входящий сигнал;
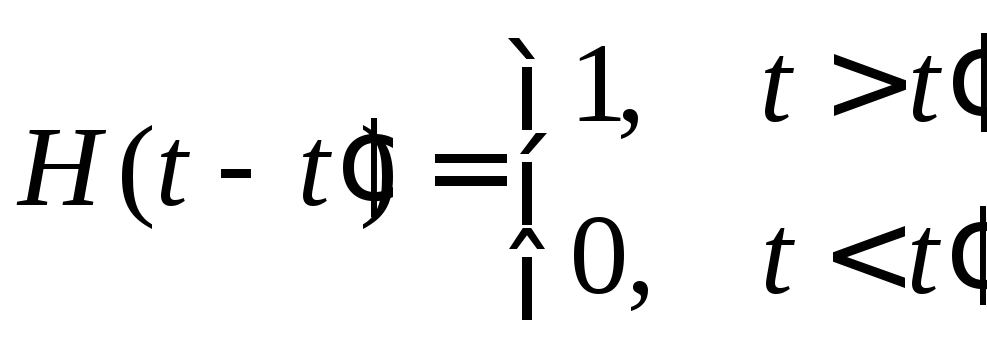 –функция
включения;
–функция
включения;
![]() –аппаратная
функция.
–аппаратная
функция.
Выходящий сигнал линейного стационарного преобразователя является сверткой входящего сигнала и функции Грина преобразователя.
Теорема о свертке
Фурье-образ свертки функций равен произведению их фурье-образов
![]() .
(1.24)
.
(1.24)
Доказательство
Используем (1.1) и (1.22)
![]() .
.
Интегралы
расцепляем заменой в первом интеграле
аргумента
![]() в виде
в виде![]() ,
,![]() .
Учитываем
.
Учитываем
![]() .
.
Получаем
![]() .
.
Для обратного преобразования Фурье выполняется
![]() .
(1.25)
.
(1.25)
Доказательство
Аналогично предыдущему доказательству получаем
![]()
![]() .
.
Под
интегралом сделана замена
![]() .
.
Теорема о произведении
Фурье-образ произведения непрерывных функций равен свертке их фурье-образов
![]()
![]() ,
,
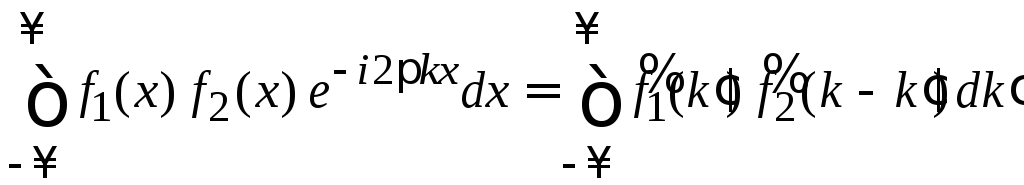 .
(1.26)
.
(1.26)
Доказательство
Выполняем фурье-преобразование (1.25), получаем
![]()
и используем интегральную теорему (1.20)
![]() .
.
Теорема о дифференцировании
При
каждом дифференцировании функции ее
Фурье-образ умножается на
![]()
![]() .
(1.35)
.
(1.35)
Доказательство
Формулу (1.2)
 ,
,
дифференцируем n раз
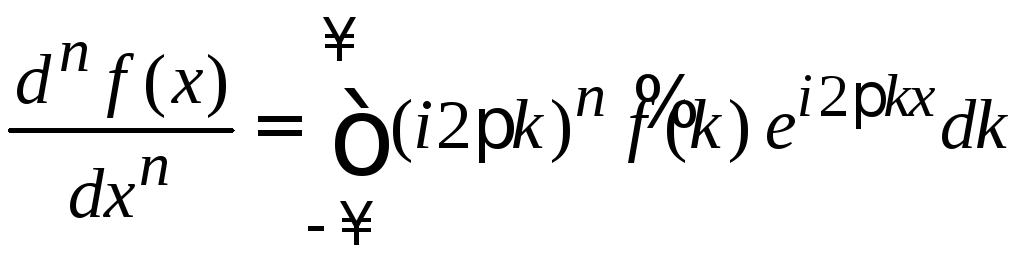 .
.
Сравниваем результат с (1.2)

для функции
 ,
получаем Фурье-образ
,
получаем Фурье-образ![]() .
.
Умножение
функции на
![]()
Умножение
функции на
![]() приводит к дифференцированию ее
фурье-образа
приводит к дифференцированию ее
фурье-образа
![]() ,
,
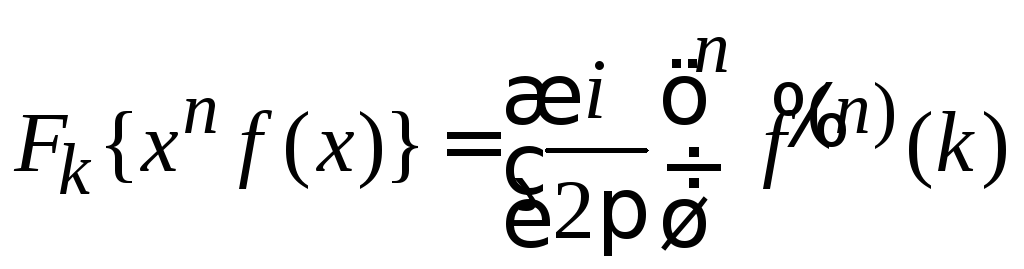 .
(1.37)
.
(1.37)
Доказательство
Дифференцируем (1.1)
 ,
,
получаем
 .
.
Сравниваем результат с формулой (1.1),
 ,
,
записанной
для функции
![]() ,
и получаем
,
и получаем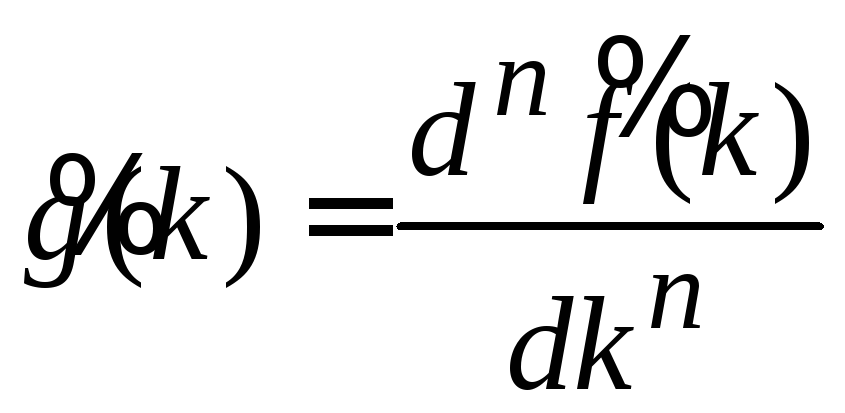 .
.
Преобразование периодическОЙ функциИ
Функция с периодом L удовлетворяет
![]() .
.
Пример показан на рисунке.
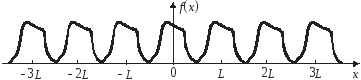
Спектр
периодической функции дискретный. Такая
функция разлагается по ортонормированному
базису гармонических функций с периодами
![]() ,
где
,
где![]() В акустике составляющая с
В акустике составляющая с
![]() называетсяосновным
тоном,
составляющие с
называетсяосновным
тоном,
составляющие с
![]() называютсяобертонами.
называютсяобертонами.
Базисы Фурье комплексных периодических функций
Условию периодичности
![]() ,
,
с
периодом
![]() удовлетворяют комплексные гармонические
функции
удовлетворяют комплексные гармонические
функции
![]() ,
,
![]()
Доказательство
Выполняется
![]() ,
,
где учтено
![]() ,
,
![]() ,
,![]()
Получаем базисы:
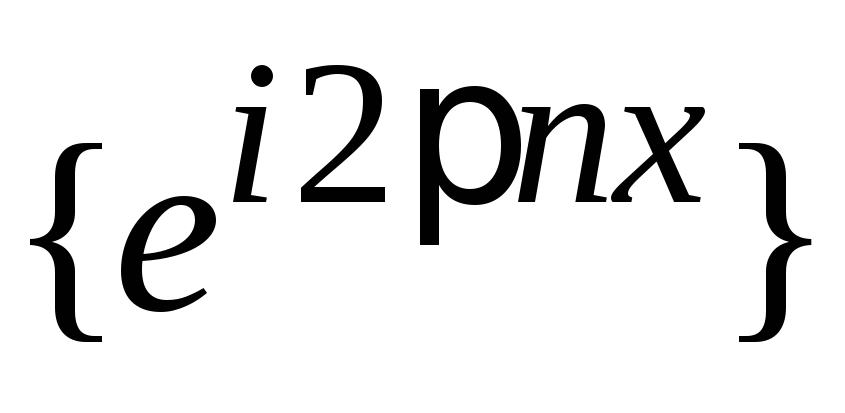 ,
,
 ,
с периодом
,
с периодом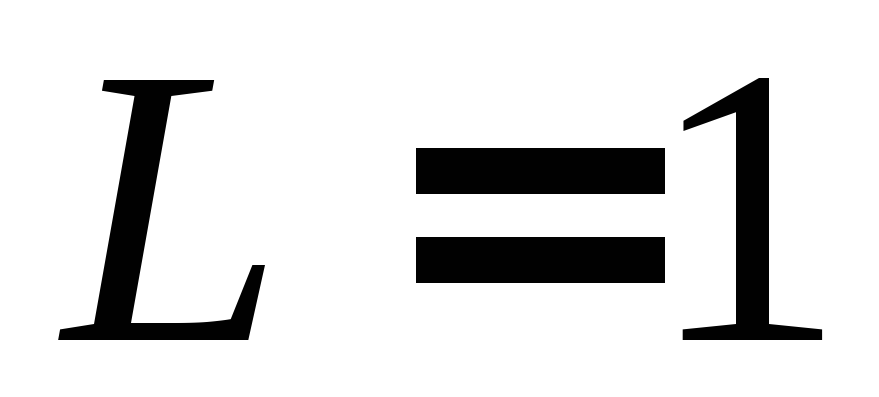 .
.
Замена аргумента дает базисы:
 :
:
 ,
, ,
с периодомL,
,
с периодомL,
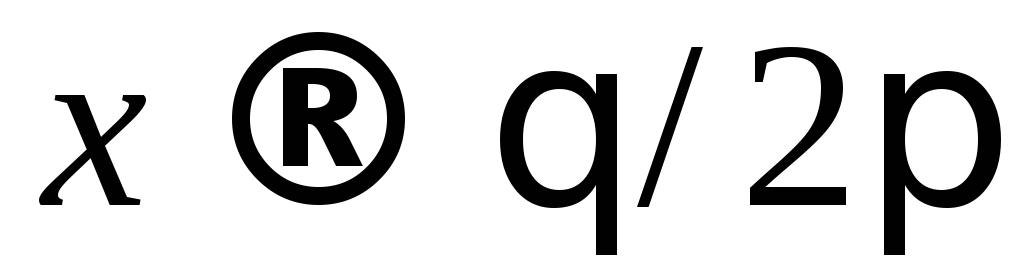 :
:
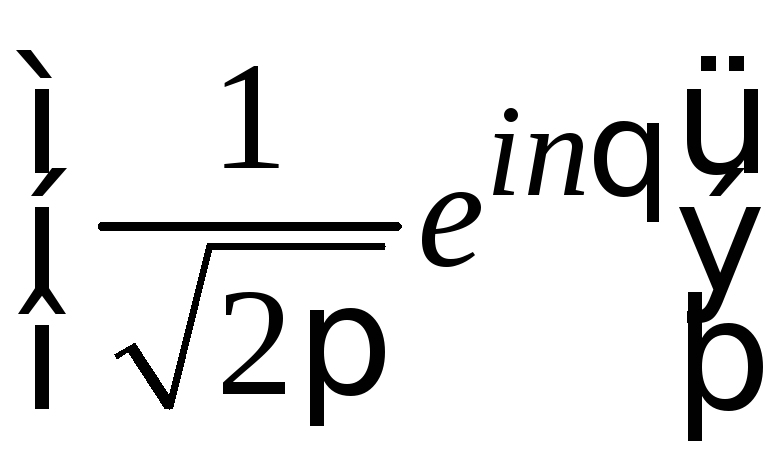 ,
, ,
с периодом
,
с периодом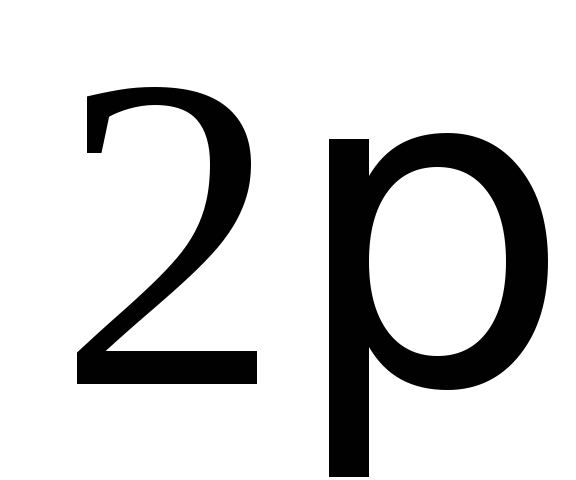 ,
,
где множитель перед экспонентой обеспечивает нормировку функции.
Базисы Фурье вещественных периодических функций
Для функций
с периодом ![]()
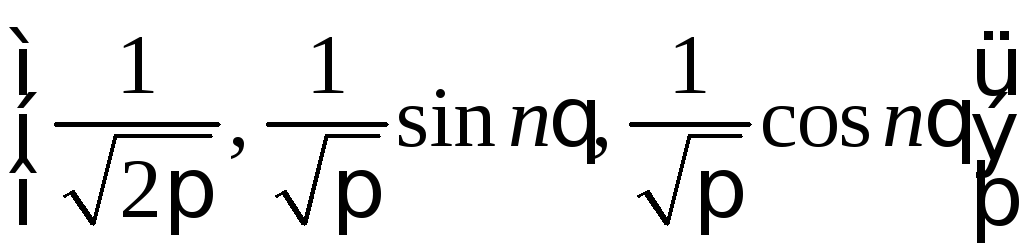 ,
,
![]()
Для
четных функций
с периодом ![]()
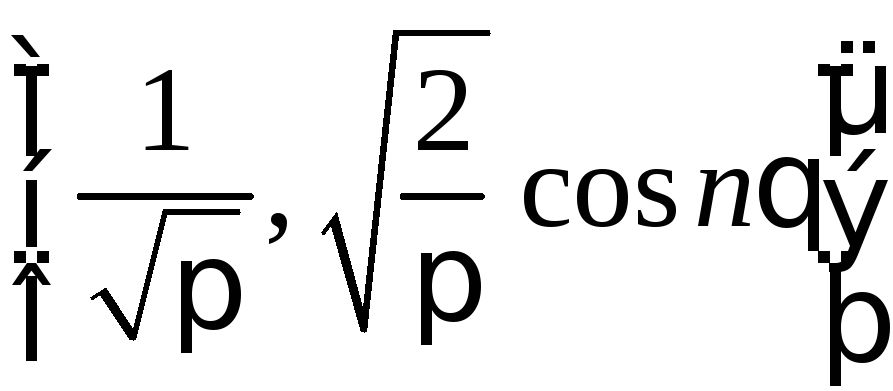 ,
,
![]()
Для
нечетных функций
с периодом ![]()
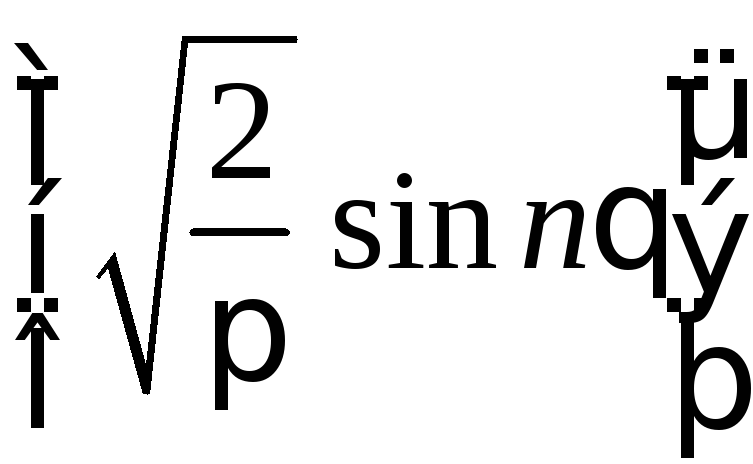 ,
,
![]()
Ортонормированность базисов
Дискретный
базис функций
![]() ,
где
,
где![]() ,
с периодомL
ортонормирован, если
,
с периодомL
ортонормирован, если
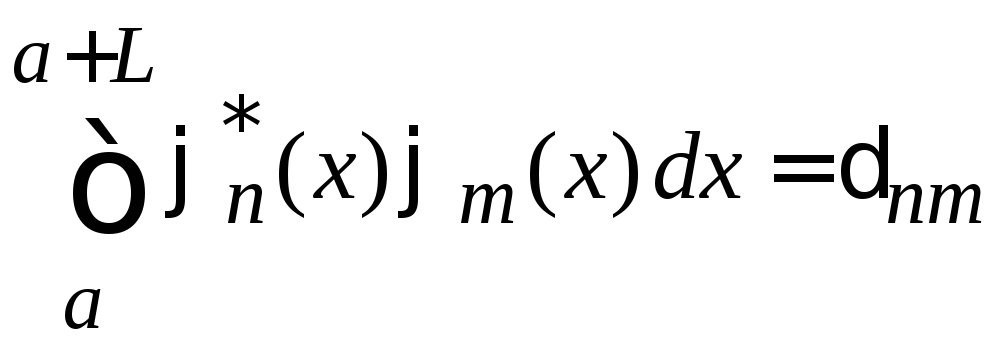 .
.
Докажем ортонормированность:
1)
Базис
![]() ,
,![]() .
Вычисляем
.
Вычисляем
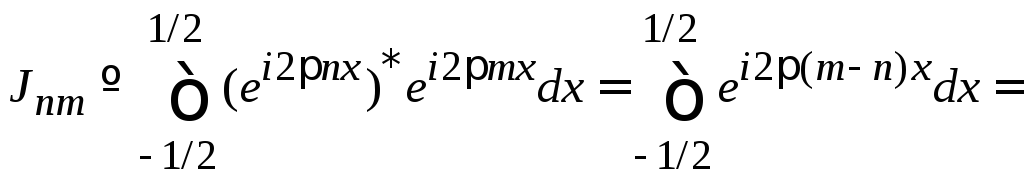
 ,
,
где использовано:
![]() ;
;
![]() ,
при
,
при
![]() ;
;
![]() .
.
2)
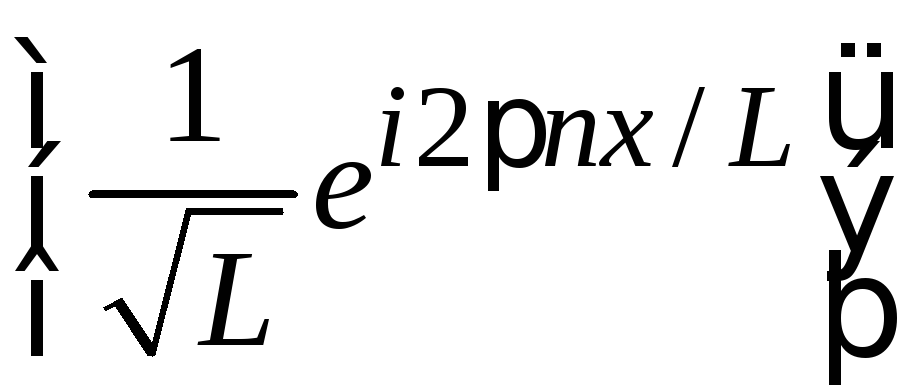 ,
,![]()
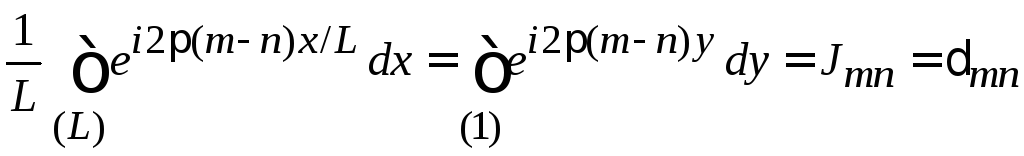 ,
(1.43)
,
(1.43)
где сделана замена
![]()
и учтено, что интеграл по периоду функции не зависит от выбора нижнего предела.
3)
 ,
,![]()
 ,
(1.44)
,
(1.44)
где сделана замена
![]() .
.
4) Доказать самостоятельно:
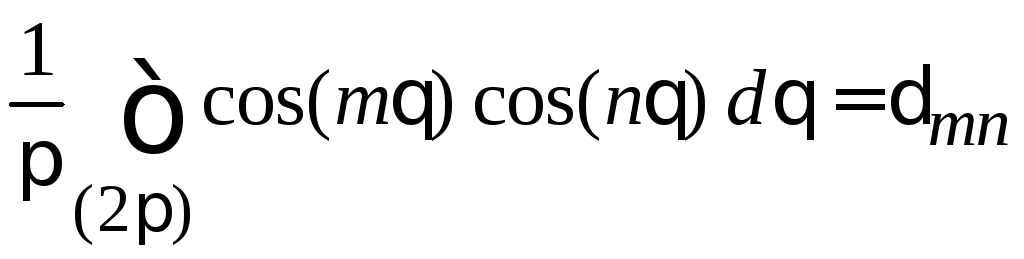 ,
,
 ,
,
 .
(1.45)
.
(1.45)
5.
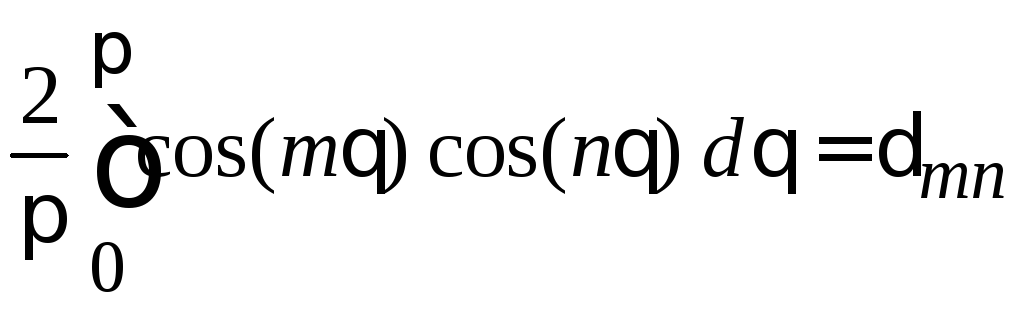 ,
,
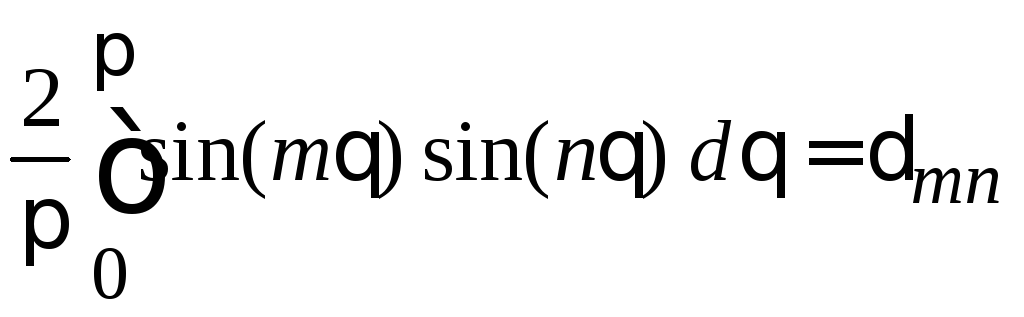 ,
,
 .
(1.46)
.
(1.46)
