Лекция 28. Свойства функций дифференцируемых на интервале

Будем рассматривать функции, непрерывные на отрезке [a; b] и дифференцируемые на интервале (a; b), т. е. во всех внутренних точках отрезка.

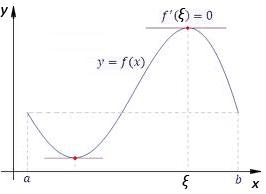
28.1.Теорема Ферма

Теорема 28.1.1. Пусть f(x) определена на интервале (a; b) и

1.в точке x0 2 (a; b) имеет наибольшее (наименьшее) значение;

2.в точке x0 существует производная функции f0(x0).

Тогда обязательно f0(x0) = 0.

Рис. 1: Иллюстрация к теореме Ферма.

Доказательство. Пусть для определенности f(x0) f(x) для всех x 2 (a; b), тогда

f(x0) = f(x) f(x0) 0

è

Так как существует f0(x0), то существуют односторонние пределы

lim f(x0) = f+0 (x0) 0;

x!+0 x

lim f(x0) = f0 (x0) 0;

x! 0 x

равные друг другу. Это возможно только когда

f+0 (x0) = f0 (x0) = 0 = f0(x0);

что и требовалось доказать.

1

28.2.Теорема Ролля

Теорема 28.2.1. Пусть функция f(x)

1.непрерывна на отрезке [a; b];

2.дифференцируема в интервале (a; b);

3.на концах отрезка [a; b] принимает равные значения f(a) = f(b). Тогда существует точка 2 (a; b), в которой f0( ) = 0.

Доказательство. Из непрерывности функции f на отрезке [a; b] согласно теореме Вейерштрасса следует, что f принимает в некоторых точках отрезка свои максимальное M и минимальное m значения. Если M = m, то f имеет это значение во всех точках отрезка [a; b] и производная f0(x) всюду на н¼м равна нулю.

Рис. 2: Геометрическая интерпретация теоремы Ролля.

А если M 6= m, то по крайней мере одно из этих значений f принимает во внутренней точке отрезка [a; b]. По теореме Ферма в этой точке производная f0 равна нулю и теорема

доказана.

Теорема Ролля показывает, что в некоторой точке интервала (a; b) касательная к графику функции f параллельна оси OX.

Замечание 28.1. Требования теоремы Ролля нельзя ослабить. Если хотя бы одно из трех не выполняется, то утверждение теоремы не выполняется.

Д/З: Приведите примеры, подтверждающие это замечание.

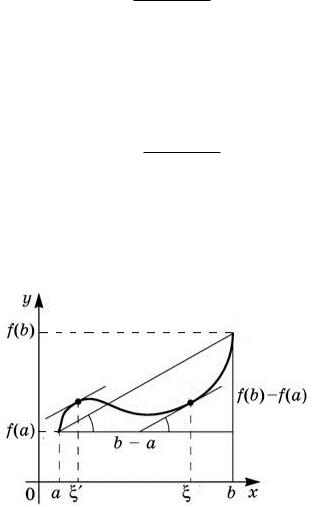
28.3.Теорема Лагранжа

Теорема 28.3.1. Пусть функция f(x)

1.непрерывна на отрезке [a; b],

2.дифференцируема в интервале (a; b),

тогда существует точка 2 (a; b) такая, что

2

Доказательство. Подбер¼м число так, чтобы для функции F (x) = f(x) x выполнялось равенство F (a) = F (b). Решив уравнение

f(a) a = f(b) b;

видим, что нужно взять

= f(b) f(a) b a

Функция F (x) непрерывна на [a; b] и дифференцируема на (a; b). Поэтому согласно теореме Ролля существует такая точка 2 (a; b), что

F 0( ) = 0:

Значит, f0( ) = 0 è

Отсюда следует равенство (28.1) и теорема доказана.

Равенство (28.1) называют ф о р м у л о й к о н е ч н ы х п р и р а щ е н и й Лагранжа. Она является одним из основных результатов дифференциального исчисления.

Используем равенство (28.2), чтобы выяснить геометрический смысл формулы конеч- ных приращений.

Рис. 3: Геометрическая интерпретация теоремы Лагранжа.

Левая часть в (28.2) равна тангенсу угла наклона касательной к графику функции f(x) в точке , а правая часть тангенсу угла наклона прямой, соединяющей точки

(a; f(a)) и (b; f(b)) графика функции. Таким образом, теорема Лагранжа показывает, что существует, по крайней мере, одна точка 2 (a; b), касательная в которой параллельна прямой, соединяющей точки (a; f(a)) и (b; f(b)). Для функции, график которой изображен на рисунке 3, утверждение теоремы выполняется в точках и 0.

Âформуле 28.1 не обязательно a < b, она имеет место и при a > b, так как вместе

ñ(28.1) выполняется равенство

f(a) f(b) = f0( )(a b):

3

28.4.Следствия из теоремы Лагранжа

Следствие 28.4.1. Формула 28.1 может быть записана в виде

наглядно поясняющем ее название формула к о н е ч н ы х п р и р а щ е н и й.

Доказательство. Пусть функция дифференцируема в окрестности точки x0, точка x0 + x принадлежит этой окрестности. Положив в формуле 28.1 значения a и b равными сответственно x0 è x0 + x, получим

f(x0 + x) f(x0) = f0( ) x;

где некоторое число из интервала (x0; x0 + x). Приращение x может быть и отрицательным, в этом случае точка x0 + x расположена левее x0 на действительной оси, лежит между ними. Следствие доказано.

Замечание 28.1. Заметим, что формула (28.3) отличается от известного приближенного равенства f(x0) f0(x0) x.

Следствие 28.4.2. Пусть функция f(x)

1.непрерывна на отрезке [a; b],

2.f0(x) = 0 äëÿ âñåõ x 2 (a; b);

тогда функция f постоянна на [a; b].

Доказательство. Для каждой пары точек x и x из [a; b] согласно формуле конечных приращений Лагранжа между x и x имеется точка такая, что

f(x ) f(x ) = f0( )(x x ):

Так как принадлежит интервалу (a; b), то f0( ) = 0 и, значит, f(x ) = f(x ):

Теорема доказана, так как x и x произвольные точки отрезка [a; b].

Следствие 28.4.3. Пусть функции f(x) и g(x)

1.непрерывны на отрезке [a; b],

2.дифференцируемы в интервале (a; b),

3.8x 2 (a; b) f0(x) = g0(x).

Тогда функции f и g отличаются на постоянную:

f(x) = g(x) + c; c const:

Доказательство. Функция F (x) = f(x) g(x) удовлетворяет всем требованиям леммы 28.4.2, следовательно, F (x) c на отрезке [a; b], где c некоторая постоянная. Тогда f(x) = g(x) + c, что и требовалось доказать.

Следствие 28.4.4. Пусть функция f(x)

4

1.непрерывна на промежутке [x0; b), содержащем точку x0 (b > x0);

2.дифференцируема в интервале (x0; b);

Доказательство. Дадим аргументу функции f приращение x в точке x0 так, чтобы выполнялось неравенство x = x0 + x < b. Согласно следствию 28.4.1 приращение функции f в точке a можно представить в виде (28.3). Поделив обе части равенства (28.3) наx и перейдя к пределу при x ! +0, получим

lim f(x0) = lim f0( ):

x!+0 x x!+0

Рассмотрим правую часть этого предельного равенства.

Òàê êàê x0 < < x0 + x è x ! +0, òî ! x0 + 0 при x ! +0. Тогда

В силу выполнения условия (3) имеем

lim f0( ) = A;

!x0+0

тогда существует конечный предел

lim f(x0) = A;

x!+0 x

что и требовалось доказать. Замечание 28.2. Если функция f(x)

1.непрерывна на промежутке (b; x0], содержащем точку x0 (b < x0);

2.дифференцируема в интервале (b; x0);

3. существует конечный предел lim f0(x) = A;

x!x0 0

то существует левая производная f0 (x0) = A.

Следствие 28.4.5. Производная функции, дифференцируемой на интервале, не может иметь точек разрыва первого рода.

Доказательство. Предположим, что производная функции f, дифференцируемой на интервале (a; b) имеет в точке x0 2 (a; b) разрыв первого рода, т. е.

В первом случае согласно следствию 28.4.4 получим f+0 (x0) 6= f0 (x0), что противоречит дифференцируемости f(x) в точке x0 2 (a; b). Во втором случае получим противоречие следствию 28.4.4.

5