Лекция 31. Формула Тейлора

31.1.Формула Тейлора

Известно, что наиболее простыми функциями в смысле вычисления являются много- члены. Возникает вопрос о возможности замены функции f в окрестности точки x мно-

гочленом некоторой степени.

Из определения дифференцируемости функции f в точке x0 следует, что если y = f(x) дифференцируема в точке x0, то ее приращение в некоторой достаточно малой окрестности U (x0) можно представить в виде

f(x0) = f0(x0) x + o ( x) ;

где o( x) бесконечно малая более высокого порядка малости, чем x при x ! 0, т. е. f(x) = f(x0) + f0(x0) (x x0) + o (x x0) 8x 2 U (x0):

Другими словами, существует многочлен первой степени

P1(x) = f(x0) + a1(x x0);

такой что при x ! x0

f(x) = P1(x) + o(x x0);

причем P1(x) удовлетворяет следующим условиям: P1(x0) = f(x0), P10(x0) = a1 = f0(x0). Обозначим, через r1(x) разность значений данной функции f(x) и построенного мно-

гочлена P1(x):

r1(x) = f(x) P1(x):

Рис. 1: Погрешность при замене функции f(x) многочленом P1(x).

r1 = o(x x0) есть погрешность, возникающая при замене функции y = f(x) многочленом P1(x). Для значений из окрестности U (x0), для которых погрешность r1(x) достаточно мала, многочлен P1(x) дает приближенное представление функции.

Таким образом, зная значение функции и производной в точке x0 можно приближенно вычислить значение функции в окрестности U (x0). Предположим, что в точке x0 извест- ны n производных функции f в точке x0. Какую информацию о характере поведения функции они несут?

1

Рассмотрим сначала в качестве функции f многочлен Q(x) степени n относительно переменной x. Запишем его как многочлен по степеням x x0:

n

X

Q(x) = ak(x x0)k = a0 + a1(x x0) + a2(x x0)2 + : : : + an(x x0)n:

k=0

и покажем, что коэффициенты ak можно выразить через значения производных много- члена Q(x) в точке x0. Так как производные функции Q(x) имеют вид:

Q0(x) = a1 + 2a2(x x0) + 3a3(x x0)2 + : : : + nan(x x0)n 1;

Q00(x) = 2!a2 + 3 2a3(x x0) + 4 3a4(x x0)2 + : : : + n(n 1)an(x x0)n 2;

: : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : :

Qk(x) = k!ak + (k + 1)!(x x0) + : : : + n(n 1) : : : (n k + 1)an(x x0)n k;

: : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : :

Qn(x) = n!an;

òî Q(k)(x0) = k!ak, k = 0; n, и все коэффициенты многочлена Q(x) выражаются через

Q(k)

значения производных функции Q(x) в точке x0: ak = k! , k = 0; n. Нулевая производная есть значение функции в точке: Q(0)(x0) = Q(x0). Многочлен n-го порядка полностью

определяется своими производными:

Для произвольной функции f(x), имеющей в точке x0 производные до порядка n вклю- чительно, построим многочлен

ð à ï î ð ÿ ä ê à n ô ó í ê ö è è f(x) â î ê ð å ñ ò í î ñ ò è ò î ÷ ê è x0.

Обозначим, через rn(x) разность значений функции f(x), имеющей в точке x0 произ- водные до порядка n включительно, и е¼ многочлена Тейлора порядка n:

rn(x) есть погрешность, возникающая при замене функции y = f(x) многочленом Pn(x). Для значений из окрестности U (x0), для которых погрешность rn(x) достаточно мала, многочлен Pn(x) дает приближенное представление функции (рис. 2).

Определение 31.1. Равенство

2

Рис. 2: Погрешность при замене функции f(x) многочленом Pn(x).

Формулу Тейлора при x0 = 0 нередко называют формулой Маклорена.

Пример 31.1. Представить функцию f(x), заданную параметрически уравнениями

Точка x0 = 0 соответствует значению параметра t = =2. Определяем значение

вого и первого порядка:

P0(x) = P1(x) = 1;

а также многочлены Тейлора второго и третьевого порядка:

P2(x) = P3(x) = 1 12x2:

Íà ðèñ. 3 изображены графики функции f(x) и ее многочленов Тейлора до третьего порядка включительно в окрестности точки x0 = 0.

3

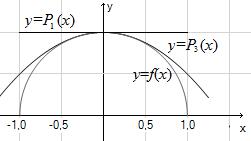
Рис. 3: Графики функции f(x) и ее многочленов Тейлора в окрестности точки x0 = 0.

4