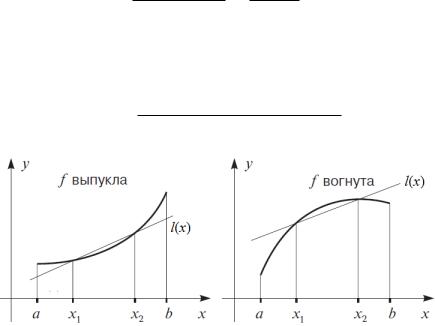
Лекция 35. Выпуклость функции

35.1.Определения

Пусть функция f(x) определена на интервале (a; b) и x1; x2 2 (a; b). Проведем прямую через точки с координатами (x1; f(x1)) è (x2; f(x2)), лежащие на графике функции f(x). Уравнение прямой, проходящей че- рез две точки:

Обозначим l(x) соответствие y(x), задаваемое уравнением (35.1), тогда

èç (35.1) получаем, что прямую, проходящую через точки с координатами (x1; f(x1)) è (x2; f(x2)), задает функция

l(x) = f(x2)(x x1) + f(x1)(x2 x): x2 x1

Рис. 1: Выпуклая и вогнутая функции.

Определение 35.1. Функция f(x) называется в ы п у к л о й или в ы - п у к л о й в н и з на интервале (a; b), если для любых точек x1; x2 2(a; b) и любой точки x 2 (x1; x2) выполняется неравенство f(x) l(x); то есть все точки графика f, соответствующие x 2 (x1; x2), расположены ниже отрезка с концами в точках (x1; f(x1)) è (x2; f(x2)), или на этом отрезке.

Определение 35.2. Функция f(x) называется в о г н у т о й или в ы - п у к л о й в в е р х на интервале (a; b), если для любых точек x1; x22(a; b) и любой точки x 2 (x1; x2) выполняется неравенство f(x) l(x); то есть все точки графика f, соответствующие x 2 (x1; x2), расположены выше отрезка с концами в точках (x1; f(x1)) è (x2; f(x2)), или на этом отрезке.

1

Определение 35.3. Функция f(x) называется с т р о г о в ы п у к л о й в н и з (с т р о г о в ы п у к л о й в в е р х) на интервале (a; b), если для любых точек x1; x2 2 (a; b) и любой точки x 2 (x1; x2) выполняется неравенство f(x) < l(x) (f(x) > l(x)):

Всякий интервал на котором функция (строго) выпукла вниз (вверх) называется интервалом (строгой) выпуклости вниз (вверх) этой функции.

Необходимые и достаточные условия выпуклости

Теорема 35.1.1 (Первый критерий выпуклости). Пусть функция f(x)

дважды дифференцируема на интервале (a; b). Для того чтобы она была выпуклой вниз (вверх) на интервале (a; b) необходимо и достаточно, чтобы f00(x) 0 (f00(x) 0) äëÿ âñåõ x 2 (a; b).

Доказательство. Достаточность. Сравним значения f(x) и l(x) для x; x1; x2 2 (a; b) таких, что a < x1 < x < x2 < b:

f(x) l(x) = f(x) f(x2)(x x1) + f(x1)(x2 x) = x2 x1

= f(x)((x2 x) + (x x1)) f(x2)(x x1) f(x1)(x2 x) = x2 x1

= (f(x) f(x1))(x2 x) + (f(x) f(x2))(x x1): x2 x1

Применяя теорему Лагранжа, получаем

f(x) l(x) = f0( )(x x1)(x2 x) + f0( )(x x2)(x x1) = x2 x1

= (x x1)(x2 x)[f0( ) f0( )]; x2 x1

ãäå x1 < < x < < x2. Так как по условию теоремы функция f0(x) непрерывна на любом [ ; ] (a; b) и дифференцируема на ( ; ),

то применим теорему Лагранжа к приращению производной:

ãäå < < .

2

Поскольку x x1 > 0, x2 x > 0, < 0, тогда, если f00(x) 0 на (a; b), а, значит, и f00( ) 0, то f(x) l(x) 0. Итак, в этом случае

функция f(x) выпуклая или выпуклая вниз. Если же f00(x) 0 на (a; b), а, значит, и f00( ) 0, то f(x) l(x) 0, то есть функция f(x) вогнутая

или выпуклая вверх.

Необходимость. Пусть f(x) выпукла вниз, т. е. для любых x1; x2 2(a; b)

и любой точки x 2 (x1; x2) выполняется неравенство f(x) l(x) 0, то из равенства (35.2), ãäå x1 < < < < x2, получим, что f00( ) 0. В силу произвольности x1; x2 2 (a; b) делаем вывод о том, что f00(x) 0 äëÿ

всех x 2 (a; b). Аналогично доказывется, что, если f(x) выпукла вверх, то f00(x) 0 äëÿ âñåõ x 2 (a; b).

Теорема доказана.

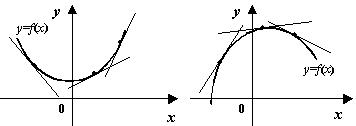
Замечание 35.1. Связь знака f00(x) на (a; b) с типом выпуклости f(x) на этом интервале легко запомнить, если заметить, что случай f00(x) 0 соответствует рту позитивного смайлика, а случай f00(x) 0 рту негативного смайлика (рис. 3).

Рис. 2: Выпуклая и вогнутая функции.

Теорема 35.1.2. Åñëè f00(x) > 0 (f00(x) < 0) для всех x 2 (a; b), то функция f(x) строго выпукла вниз (вверх) на этом интервале.

Доказательство аналогично доказательству достаточности предыдущей теоремы.

Замечание 35.2. Утверждение, обратное теореме 35.1.2 несправедливо. Например, f(x) = x4 строго выпукла вниз, но f00(x) = 12x2 = 0 ïðè

x = 0. Значит, если f(x) строго выпукла вниз (вверх) на интервале (a; b), то это не значит, что f00(x) < 0 (f00(x) > 0) äëÿ âñåõ x 2 (a; b).

Замечание 35.3. Отметим, что если функция f (строго) выпукла вверх (вниз) на интервале (a; b), то функция f (строго) выпукла вниз (вверх) на этом интервале.

3

Теорема 35.1.3 (Второй критерий выпуклости). Пусть функция f(x)

имеет на интервале (a; b) производную f00(x). Функция f(x) выпукла вниз (вверх) на (a; b) тогда и только тогда, когда график y = f(x) лежит при x 2 (a; b) не ниже (не выше) любой касательной

y = f(x0) + f0(x0)(x x0);

провед¼нной при любом x0 2 (a; b), то есть выполняется неравенство

f(x) > f(x0)+f0(x0)(x x0) f(x) 6 f(x0)+f0(x0)(x x0) 8x; x0 2 (a; b):

Рис. 3: Связь выпуклости функции f(x) с касательной к графику f(x).

Доказательство. Ординаты точек на касательной к графику f(x) в точке x0 задаются с помощью функции L(x) = f(x0) + f0(x0)(x x0).

Применяя теорему Лагранжа к разности f(x) f(x0), получаем:

f(x) L(x) = (f(x) f(x0)) f0(x0)(x x0) = f0( )(x x0) f0(x0)(x x0) = (f0( ) f0(x0))(x x0); ãäå a < x0 < b, a < x < b, а точка лежит

между x и x0.

Применяя еще раз теорему Лагранжа, но уже к приращению производной f0( ) f0(x0), получим

f(x) L(x) = f00( )( x0)(x x0);

где точка лежит между и x0.

Точка лежит между x и x0: 2 (x; x0) èëè 2 (x0; x), но в любом

случае ( x0)(x x0) > 0. В силу этого знак разности f(x) L(x) совпадает (при x 6= x0), со знаком f00( ) и, значит, со знаком f00(x) íà (a; b)

в силу произвольности выбора точек x; x0 2 (a; b). Согласно первому критерию выпуклости это и означает то, что требовалось доказать.

Теорема 35.1.4. Åñëè f00(x) > 0 (f00(x) < 0) для всех x 2 (a; b), то график y = f(x) лежит при x 2 (a; b) выше (ниже) любой касательной

4

y = f(x0) + f0(x0)(x x0) (за исключением x = x0), провед¼нной при любом x0 2 (a; b), то есть выполняется неравенство

f(x) > f(x0) + f0(x0)(x x0) 8x; x0 2 (a; b); x 6= x0

f(x) < f(x0) + f0(x0)(x x0) 8x; x0 2 (a; b); x 6= x0 :

Доказательство аналогично доказательству достаточности предыдущей теоремы.

Замечание 35.4. Утверждение, обратное теореме 35.1.4 несправедливо. Объясните, почему?

Пример 35.1. Найти промежутки выпуклости определенного знака функции f(x) = 3x2 x3; ãäå x 2 R.

Вторая производная f00(x) = 6(1 x) положительна при x < 1 и отрицательна при x > 1. Следовательно, согласно досмтаточному условию строгой выпуклости, на интервале ( 1; 1) функция f(x) выпукла вниз, а на интервале (1; +1) выпукла вверх.

5