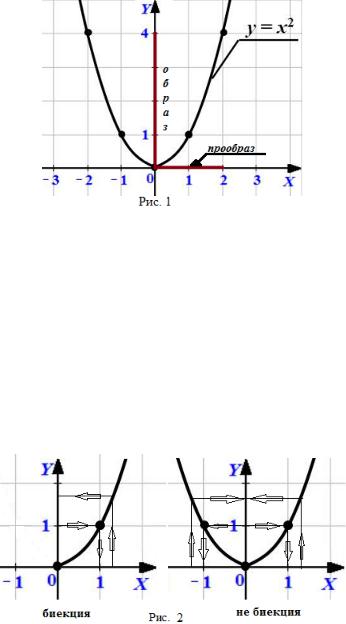
Лекция 5. Свойства функций; элементарные функции

5.1.Взаимно-однозначные функции: понятие обратной функции

Пусть задано отображение f : X ! Y . В случае, когда Y = X, говорят, что отображение f переводит множество X в себя, а именно f : X ! X.

Пусть A X, тогда о б р а з о м этого множества при отображении f называют множество B = f(A) = fy : y 2 E(f); y = f(x) 8 x 2 Ag. Множество A называют п р о о б р а - з о м множества B.

Пример 5.1. При отображении y = x2 образом отрезка [0; 2] является отрезок [0; 4]. Отрезок [0; 2] называется прообразом отрезка [0; 4]. Отрезок [ 2; 0] также является прообразом отрезка [0; 4] при отображении y = x2.

Это определение можно сформулировать иначе.

Определение 5.2. Функция f(x) называется в з а и м н о - о д н о з н а ч н о й ( f б и - е к ц и я), если 8 x1; x2 2 X таких, что x1 6= x2 выполняется соотношение f(x1) 6= f(x2).

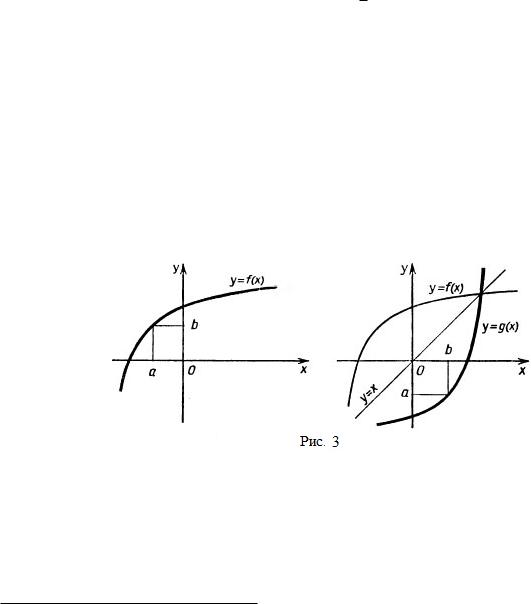
Иллюстрация этих определений представлена на рис. 2. Каждая прямая y = y0, ãäå y0 2 Y , пересекает график взаимно-однозначной функции в единственной точке x0; y0, ãäå f(x0) = y0.

1

Определение 5.3. Пусть на множестве X задана функция y = f(x), множеством зна- чений которой является множество Y . Если f биекция, то на множестве Y опредена функция x = f 1(y), ставящая в соответствие каждому y 2 Y то значение x из X, для которого f(x) = y. Функция x = f 1(y) называется о б р а т н о й1 для функции y = f(x).

Согласно этому определению D(f 1) = Y , E(f 1) = X, т. е. множества определения

и значений исходной и обратной функции меняются местами. Функцию, имеющую обратную, называют о б р а т и м о й.

Из определения обратной функции следует, что

8 x 2 E(f) f(f 1(x)) = x;

8 x 2 D(f) f 1(f(x)) = x:

Отметим, что если x = f 1(y) обратная для y = f(x), то, очевидно, функция y = f(x) является обратной для функции x = f 1(y). Поэтому функции y = f(x) и x = f 1(y)

называют также в з а и м н о - о б р а т н ы м и.

Функции y = x2, x 0, è x = py являются взаимно-обратными, а для функции y = x2 при x 2 R нельзя определить обратную функцию, так как y = x2 íå

является взаимно-однозначной функцией на естественной области определения (см. рис. 2 ¾не биекция¿).

Очевидно, что график функции x = f 1(y) совпадает с графиком функции y = f(x). Обозначая, как обычно, аргумент обратной функции x, а значение y, ее записывают в

âèäå

y = f 1(x); x 2 D(f 1):

График этой функции симметричен графику функции y = f(x), x 2 D(f), относительно прямой y = x. При построении графика обратной функции точки с координатами (a; b) 2 f переходят в точки (b; a) 2 f 1. На рис. 3 представлены графики функций f(x) и g = f 1(x) взаимно обратных друг к другу.

5.2.Свойства функций

Четность. Функцию f(x), определенную на симметричном относительно нуля множестве X, называют ч е т н о й, если для любого x 2 X верно равенство

f( x) = f(x);

1Заметим, что f 1 это не ¾минус первая степень¿ функции f, а символическое обозначение функции, обратной для f.

2

н е ч е т н о й, если для любого x 2 X верно равенство

f( x) = f(x):

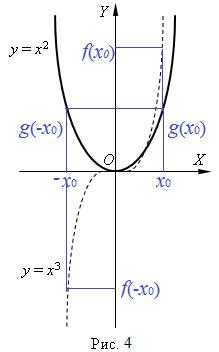
График четной функции симметричен относительно оси ординат, график нечетной функции симметричен относительно начала координат. Примеры графиков четной ( g(x) = x2)

и нечетной (f(x) = x3) функций изображены на рис. 4.

Монотонность. Функцию f называют в о з р а с т а ю щ е й (н е у б ы в а ю щ е й) на множестве X D(f), если для любых x1; x2 2 X из неравенства x1 < x2 следует неравен- ñòâî f(x1) f(x2). Это определение коротко записывают так:

8 x1; x2 2 X; x1 < x2 ) f(x1) f(x2):

Функцию f называют у б ы в а ю щ е й (н е в о з р а с т а ю щ е й) на множестве X D(f),

åñëè

8 x1; x2 2 X; x1 < x2 ) f(x1) f(x2):

Если в этих определениях из неравенства x1 < x2 следует строгое неравенство f(x1) < f(x2) (соответственно f(x1) > f(x2)), то функцию называют с т р о г о в о з р а с - т а ю щ е й (соответственно с т р о г о у б ы в а ю щ е й) на множестве X.

Возрастающие и убывающие функции объединяют названием м о н о т о н н ы е, строго возрастающие и строго убывающие с т р о г о м о н о т о н н ы е.

Если X = D(f), то указание на множество X опускают.

Примером строго возрастающей функции является функция y = x3, x 2 R (см. рис. 1). Функция y = x2, x 2 R (см. рис. 1), строго убывает на ( 1; 0) и строго возрастает на (0; +1), на всей области определения R она не является монотонной.

Периодичность. Число T 6= 0 называют п е р и о д о м функции f, если для любого x 2 D(f) выполнено f(x + T ) = f(x):

Если T период функции, то для любого k 2 Z, k 6= 0, число kT также является

периодом этой функции. Наименьший положительный период функции называется о с - н о в н ы м (или г л а в н ы м) периодом.

3

Функцию, имеющую главный период, будем называть п е р и о д и ч е с к о й. Примером периодической функции является функция, ставящая в соответствие каждому x 2 R

дробную часть2 числа x. Период данной функции любое целое число, отличное от нуля; основной период равен единице. График функции y = fxg представлен на рис. 5.

Пример 5.3. Периодом постоянной функции y = const является любое действительное число, т. е. множество положительных периодов этой функции есть полупрямая (0; +1).

Точная нижняя грань3 этого множества есть число ноль, ноль не принадлежит этому множеству, следовательно, наименьшего элемента в этом множестве нет. Такую функцию согласно данному определению мы не можем назвать периодической функцией.

Пример 5.4. Периодом функции Дирихле4 является любое рациональное число. По тем же причинам, что и в предыдущем примере мы не будем называть функцию Дирихле периодической5 функцией.

5.3.Арифметические операции над функциями

Пусть функции f(x) и g(x) заданы на некотором множестве X. Над этими функци-

ями определены четыре арифметических операции: сложение, вычитание, умножение и деление.

С л о ж е н и е м функций f(x) и g(x) называется операция, которая каждому x 2 X ставит в соответствие значение y = f(x)+g(x). Результат сложения называется с у м м о й

функций.

В ы ч и т а н и е м функций f(x) и g(x) называется операция, которая каждому x 2 X ставит в соответствие значение y = f(x) g(x). Результат вычитания называется р а з -

íо с т ь ю функций.

Óм н о ж е н и е м функций f(x) и g(x) называется операция, которая каждому x 2 X

ставит в соответствие значение y = f(x) g(x). Результат умножения называется п р о -

èз в е д е н и е м функций.

Äе л е н и е м функций f(x) и g(x) называется операция, которая каждому x 2 X

ставит в соответствие значение y = f(x)=g(x). Результат деления называется ч а с т н ы м функций. Область определения частного функций f и g есть множество X за исключением точек, в которых g(x) = 0.

2y = fxg дробная часть числа x; fxg = x [x], ãäå [x] целая часть числа. Подробнее см. лекцию 3

и лекцию 4.

3См. лекцию 3: Ограниченные множества, точные грани множества.

4Значение функции D(x) равно 1, åñëè x число рациональное, и 0, åñëè x число иррациональное.

5В некоторых источниках определение периодической функции вводится несколько иначе: периодиче- ской называют функцию, имеющую период. Согласно такому определению функции y = const и функция

Дирихле будут периодическими, но не имеющими основного периода.

4

5.4.Элементарные функции и их классификация

К о с н о в н ы м э л е м е н т а р н ы м функциям относят постоянную, степенную, показательную, логарифмическую, тригонометрические и обратные тригонометри- ческие функции.

Э л е м е н т а р н о й ф у н к ц и е й называют функцию, которая может быть задана с помощью конечного числа арифметических операций и композиций из основных элемен-

Пример 5.6. Функция Дирихле, y = sgn x, функции целая часть числа, дробная часть числа элементарными не являются.

Удобно классификацию элементарных функций представить в виде таблицы. Элементарные функции:

Трансцендентные

Алгебраические

Иррациональные

Рациональные

Целые рациональные

Дробные рациональные

Ц е л а я р а ц и о н а л ь н а я ф у н к ц и я (алгебраический многочлен или полином)функция вида

Pn(x) = a0 + a1x + a2x2 + : : : + anxn;

ãäå n 2 N, ai 2 R, i = 1; n, определенная для всех x 2 R.

Pn(x)

Д р о б н а я р а ц и о н а л ь н а я ф у н к ц и я это дробь Qm(x), числителем и знаменателем которой являются некоторые рациональные функции. Областью определения

дробной рациональной функции является множество действительных чисел за исключе- нием точек, в которых выполняется равенство Q(x) = 0.

Целые рациональные и дробные рациональные функции составляют класс р а ц и о -

íа л ь н ы х функций.

Èр р а ц и о н а л ь н ы е ф у н к ц и и это степенные функции с рациональным по-

казателем и полученные из них с помощью конечного числа арифметических операций и композиций, за исключением рациональных функций.

Иррациональные и рациональные функции составляют класс а л г е б р а и ч е с к и х функций.

Т р а н с ц е н д е н т н ы е ф у н к ц и и функции, не вошедшие в класс алгебраиче-

ских. Например, все тригонометрические и обратные к ним, показательные и логарифми- ческие.

Пример 5.7. Степенная функция f(x) = x 1 относится к классу дробных рациональных функций, так как x 1 = 1=x.

5