Лекция 36. Точки перегиба, асимптоты

36.1.Точки перегиба дифференцируемой функции: необходимое условие

Пусть функция f дифференцируема при x = x0 и пусть y = L(x) уравнение касательной к графику функции f в точке (x0; f(x0)). Если разность f(x) L(x) меняет знак при переходе через точку x0, òî x0 называется точкой перегиба функции f.

Геометрический смысл точки перегиба x0 состоит в том, что график функции f(x)

переходит ("перегибается\) в точке (x0; f(x0)) с одной стороны (от наклонной) касательной в этой точке на другую (Рис. 1). Åñëè x0 точка перегиба функции, то точка (x0; f(x0))

называется точкой перегиба графика функции.

Рис. 1: Точка перегиба.

Найти точки перегиба функции f(x) = x3; ãäå x 2 R.

Вторая производная функции f00(x) = 6x положительна при x > 0 и отрицательна при x < 0. Поэтому на бесконечном интервале (1; 0) функция f строго выпукла вверх, на интервале (0; +1) она строго выпукла вниз, а точка x = 0 является одновременно

концом интервалов выпуклости вверх и вниз. Она является и точкой перегиба, поскольку уравнением касательной в ней является y = 0, и при x < 0 имеет место неравенство

f(x) < 0, а при x > 0 неравенство f(x) > 0.

Теорема 36.1.1 (Необходимое условие перегиба) . Если в точке перегиба существует вторая производная, то она равна нулю.

Доказательство. Пусть функция f имеет в точке x0 вторую производную и y = L(x)уравнение касательной к графику функции f в точке (x0; f(x0)), òî åñòü

L(x) f(x0) + f0(x0)(x x0):

Тогда, в силу формулы Тейлора,

f(x) L(x) = f00(x0)(x x0)2 + o((x x0)2); x ! x0:

2

По условию теоремы x0 точка перегиба. Если предположить, что f00(x0) 6= 0, òî

знак разности f(x) L(x) в некоторой окрестности точки x0 совпадает со знаком числа f00(x0). В этом случае разность f(x) L(x) не меняет знака в точке x0, что противоречит определению точки перегиба. Итак, если x0 точка перегиба функции f, то f00(x0) = 0.

1

Замечание 36.1. Утверждение, обратное доказанной теореме, не имеет места. Приведите пример, подтверждающий это.

Замечание 36.2. Дифференцируемая функция f может иметь точку перегиба, в которой f00 не существует. Например, производная функции

равна f0(x) = jxj. Отсюда f0(0) = 0, L(x) 0. Очевидно, что f(x) L(x) f(x) меняет знак при переходе через точку x = 0, т. е. x = 0 точка перегиба функции. При этом не существует f00(0), так как известно, что f0(x) = jxj не дифференцируема в точке x = 0.

Определение 36.2. Точку x0, в которой функция f дифференцируема, назовем в о з - м о ж н о й т о ч к о й п е р е г и б а, если f00(x0) = 0 или не существует f00(x0).

36.2.Обобщение понятия "точка перегиба\

Тогда x = x0 уравнение вертикальной касательной к графику функции f в точке (x0; f(x0)). Если разность f(x) f(x0) меняет знак при переходе через точку x0, òî x0 назовем точкой перегиба функции f в смысле обобщения. При этом график функции f(x)

переходит в точке (x0; f(x0)) с одной стороны (от вертикальной) касательной в этой точке на другую (Рис. 2) аналогично случаю на рис. 1.

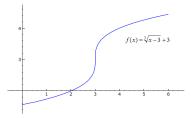
Рис. 2: Точка перегиба в смысле обобщения.

2

Таким образом, для любых x<3, x0 <3 (x6=x0) рассматриваемая разность f(x) L(x)>0,

выпуклости вверх. Согласно второму критерию выпуклости f(x) f(x0) f0(x0)(x x0) 0

Поэтому эта точка не является точкой перегиба даже в смысле обобщения. График функ-

ции имеет вертикальную касательную в точке x = 0, и его ветви, для котрых x > 0 и

0 p

x < 0, лежат по разные стороны от нее, но разность f(x) f(0) = 3 x2 0 не меняет знак.

Условно говоря, график в точке x = 0 не перегибается, а \, поэтому точки такого типа называются т о ч к а м и в о з в р а т а. "возвращается назад

2См. лекцию 25, пункт 3.

3

Рис. 3: Точка возврата.

36.3.Достаточные условия точки перегиба

Теорема 36.3.1 (Первое достаточное условие точки перегиба) . Если функция f(x) диффе-

ренцируема в точке x0, дважды дифференцируема в некоторой проколотой окрестности U0(x0) этой точки и вторая производная f00(x) меняет знак при переходе через точку x0, òî x0 является точкой перегиба функции f.

Доказательство. Представим уравнение касательной к графику функции f в точке x0 как y = L(x). Аналогично тому, как это было сделано в доказательстве второго критерия выпуклости функции, применим теорему Лагранжа к разности f(x) f(x0) в разности f(x) L(x):

f(x) L(x) = (f(x) f(x0)) f0(x0)(x x0) = f0( )(x x0) f0(x0)(x x0) =

= (f0( ) f0(x0))(x x0);

ãäå a < x0 < b, a < x < b, а точка лежит между x и x0. Применяя еще раз теорему Лагранжа, но уже к приращению производной f0( ) f0(x0), получим

f(x) L(x) = f00( )( x0)(x x0);

где точки x и лежат по одну сторону от точки x0, поэтому при x 6= x0 имеем

( x0)(x x0) > 0 и, следовательно, sign[f(x) L(x)] = signf00( ):

Точка лежит между и x0, то есть по ту же сторону от x0, что и точка x. Отсюда имеем, что если f00 меняет знак при переходе через точку x0, то разность f(x) L(x)

меняет знак и, следовательно, x0 является точкой перегиба.

Теорема 36.3.2 (Второе достаточное условие точки перегиба) . Пусть f00(x0) = 0, è f000(x0) 6= 0; тогда x0 является точкой перегиба.

Доказательство. По формуле Тейлора, в силу условия f00(x0) = 0, имеем

f(x) = f(x0) + f0(x0)(x x0) + f000(x0)(x x0)3 + o((x x0)3); x ! x0; 3!

и, поскольку L(x) = f(x0) + f0(x0)(x x0),

f(x) L(x) = f000(x0)(x x0)3 + o((x x0)3); x ! x0:

3!

Отсюда следует, что знак разности f(x) L(x) меняется при изменении знака x x0. Это означает, что точка x0 является точкой перегиба. Что и требовалось доказать.

4

êàõ x = 1

p

2 и при переходе через них меняет знак. Следовательно, согласно первому достаточному условию, эти точки являются точками перегиба (Рис.3).

Ðèñ. 4: y = ln(x 2).

Замечание 36.1. Прямая x = a не может быть вертикальной асимптотой, если функция непрерывна в точке x = a. Поэтому вертикальные асимптоты следует искать в точках разрыва функции или на границе области определения.

Определение 36.4. Пусть функция f определена на бесконечном интервале (a; +1). Говорят, что прямая l(x) = kx + b является н а к л о н н о й а с и м п т о т о й графика функции y = f(x) при x ! +1, если

5

Существование наклонной асимптоты у функции при x ! +1 означает, что при стрем-

лении аргумента функции x ! +1 функция ведет себя "почти как линейная функция\, т. е. отличается от линейной функции на бесконечно малую.

Замечание 36.2. При k = 0 асимптоту называют г о р и з о н т а л ь н о й. Горизонтальная асимптота является частным случаем наклонной асимптоты.

Теорема 36.4.1 (Критерий наклонной асимптоты). Для того чтобы график функции f(x) èìåë ïðè x ! +1 наклонную асимптоту y = kx + b, необходимо и достаточно,

чтобы существовали два предельных значения

Доказательство. Необходимость. Пусть y = kx + b наклонная асимптота f(x) при x ! +1, т. е. справедливо (36.2). Тогда из связи сходящихся и бесконечно малых функций

Достаточность. Пусть существуют предельные значения (36.3). Второе из этих предельных значений дает право утверждать, что выполняется условие (36.2). Теорема доказана.

Замечание 36.3. Аналогично определяется наклонная асимптота и доказывается теорема 36.4.1 и для случая x ! 1.

Следствие 36.4.2. Для того чтобы график функции f(x) имел при x ! +1 (x ! 1) горизонтальную асимптоту y = b, необходимо и достаточно, чтобы

Замечание 36.4. На практике легче сначала проверить наличие горизонтальной асимптоты. Если, например, при x ! +1 функция имеет горизонтальную асимптоту (частный

случай наклонной), то других асимптот при x ! +1 не будет. Если же при x ! +1

функция не имеет горизонтальной асимптоты, то следует поискать наклонную, найдя пределы (36.3).

6