Лекция 25. Геометрический и физический смысл производной и дифференциала

25.1.Связь дифференцируемости функции с непрерывностью

Теорема 25.1.1. Если функция f дифференцируема в точке a, òî f непрерывна в точ- ке a.

Доказательство. Если функция f дифференцируема в точке a, то приращение функции f в точке a представляется в виде

f(a) = f0(a) x + o( x);

где o( x) бесконечно малая более высокого порядка малости, чем x при x ! 0. Приx ! 0 выражение в правой части этого равенства стремится к нулю, т. е. f(a) ! 0, а это и означает непрерывность1 функции f в точке a.

Теорема доказана.

Таким образом, для существования производной в точке необходима непрерывность функции в этой точке. Но это условие не является достаточным.

Пример 25.1. В самом деле, для приращения функции f(x) = jxj в нуле имеем f = j xj.

Значит, функция jxj не имеет производной в нуле, хотя эта функция и непрерывна всюду.

Как уже говорилось в предыдущей лекции, односторонние пределы отношения приращения функции к приращению аргумента (25.1) при x ! 0 существуют, т. е. в точке 0

функция jxj имеет левую и правую производные.

Привед¼м пример функции, непрерывной всюду, но не имеющей в некоторой точке даже односторонних производных.

стремится к нулю при x ! 0, то функция f непрерывна в нуле, а е¼ непрерывность в

остальных точках очевидна.

Так как предел отношения

fx = sin 1x

не существует ни при x ! +0, ни при x ! 0, то f не имеет в нуле даже односторонних производных.

1Функция f называется н е п р е р ы в н о й в т о ч к е a, если бесконечно малому приращению аргумента в точке a соответствует бесконечно малое приращение функции f в точке a, ò. å. f(a) ! 0 ïðè

x ! 0.

1

25.2.Геометрический смысл производной и дифференциала функции в точке

Выясним свойства графика функции, соответствующие существованию производной.

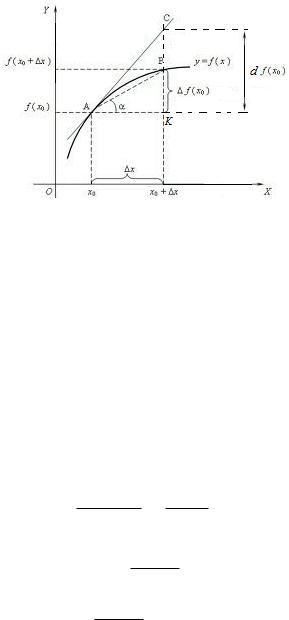
Рис. 1: Геометрическая интерпретация производной в точке.

Пусть функция f(x) непрерывна в точке x0. Будем придавать аргументу f в точке x0 малые приращения x, чтобы точки x0 + x не выходили из области определения функции.

Отметим на графике функции f (рис. 1) точки A(x0; f(x0)), B(x0 + x; f(x0 + x)) и провед¼м через эти точки прямую AB. Эту прямую называют с е к у щ е й.

Пусть угол, который прямая AB образует с осью абсцисс OX. Угол считаем положительным, если прямая AB правее точки пересечения с осью OX лежит выше оси (как на рис. 1), в противном случае считаем отрицательным. Если прямая AB параллельна оси OX, полагаем = 0.

Разным x будут соответствовать разные f(x0) и соответственно разные секущие. Напишем уравнение с е к у щ е й AB. Точка с координатами (x; y) принадлежит пря-

мой, проходящей через точки A(x0; f(x0)) è B(x0 + x; f(x0 + x)) тогда и только тогда,

когда

y f(x0) = x x0 :f(x0) x

Отсюда

y f(x0) = f(x0) (x x0) ;

x

ãäå

f(x0)

x

(25.2)

В силу непрерывности функции f в точке x0 точка B при x ! 0 приближается к точке A. При этом значение угла зависит от x: ( x).

Равенство (25.2) показывает, что существование производной f0(x0) равносильно существованию предела tg ( x) при x ! 0.

Так как на интервале ( =2; =2) тангенс является непрерывной строго монотонной функцией, существование предела tg ( x) равносильно существованию предельного зна- чения угла ( x), обозначим его 0. Значит, при x ! 0 секущая AB занимает предельное положение (на рис. 1 положение AC), соответствующее углу наклона 0 = \KAC.

Прямую, являющуюся предельным положением секущей, называют к а с а т е л ь н о й к графику функции f(x) в точке x0. Ïðè ýòîì tg 0 = f0(x0) и касательная не параллельна

оси OY , е¼ называют н а к л о н н о й.

x= x0:

Âэтом случае график функции y = f(x) в окрестности точки x0 имеет вид, схемати- чески изображенный на рис. 2-4.

Рис. 4: Вертикальные касательные.

25.4.Физический смысл производной и дифференциала

Физический смысл производной: производная это скорость изменения зависимой переменной y как функции независимой переменной x.

Предположим, что функция = f(x) описывает закон движения материальной точки по

прямой линии (т. е. зависимость пути , пройденного точкой от начала отсчета, от времени x). Тогда, как известно, разностное отношение

щей закон движения, определяет мгновенную скорость точки .

Пусть функция = f(x) определяет количество электричества y, протекшего через поперечное сечение проводника за время x. (При этом момент времени x = 0 берется за начало отсчета.) В таком случае производная f0(x) будет определять ñèëó òîêà, проходящего через поперечное сечение проводника в момент времени x.

Вообще, если функция описывает некоторый процесс, то производная характеризует скорость протекания этого процесса в данный момент.

Дифференциал показывает, как менялась бы функция (в приведенных выше примерах это путь или количество электричества), если бы в течение всего времени изменение функции проходило с той же скоростью, что и в данный момент x.

Применение дифференциалов основано на том, что в малом , т. е. при достаточно малых x, приращение дифференцируемой функции незначительно отличается от диф-

ференциала и, таким образом, при малых x дифференциал дает хорошее приближение

для приращения функции:

f(x) df(x) = f0(x) x: