Лекция 21. Непрерывность функции

21.1.Непрерывность функции в точке

Определение 21.1. Функцию f называют н е п р е р ы в н о й в т о ч к е a, если

1.a предельная точка области определения D(f);

2.для каждого " > 0 существует число (") > 0 такое, что при всех x, удовлетворяющих условию jx aj < , справедливо неравенство jf(x) f(a)j < ", короче,

8 " > 0 9 (") > 0 : 8 x jx aj < ) jf(x) f(a)j < ":

Непрерывность функции в точке свойство, характеризующее поведение функции не только в некоторой окрестности точки, но и в самой точке. Поэтому точка a обязана принадлежать области определения D(f). В этом случае в определении рассматривается

непроколотая окрестность U (a) = fx : jx aj < g точки a.

Эквивалентную формулировку получим, используя предел функции в точке.

Определение 21.2. Функция f называется н е п р е р ы в н о й в т о ч к е a, если

lim f(x) = f(a):

x!a

Определение 21.3. Функцию f называют н е п р е р ы в н о й с л е в а в т о ч к е a, если

lim f(x) = f(a):

x!a 0

1.a предельная точка области определения D(f);

2.для любой сходящейся к a последовательности точек fxng из области D(f), справед-

ливо равенство lim f(xn) = f(a).

n!1

Заметим, что когда говорят, что функция f непрерывна в точке, нет необходимости добавлять, что f определена в некоторой окрестности этой точки, поскольку это требование

уже входит в определение непрерывности.

При изучении вопросов, связанных с непрерывностью функций, полезны понятия приращения аргумента и приращения функции. Пусть a и x два значения аргумента функ-

ции f, положим x = x a. Тогда x = a + x и говорят, что точка x получена из a за сч¼т п р и р а щ е н и я а р г у м е н т а x. Разность значений функции

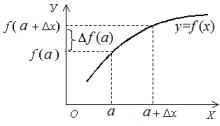
f(a) = f(a + x) f(a)

называют п р и р а щ е н и е м ф у н к ц и и f в точке a, когда аргумент получил приращение x. При этом x может быть как положительным, так и отрицательным.

Сформулируем определение непрерывности функции в точке

1

Рис. 1: f(a) = f(a + x) f(a) приращение функции f в точке a.

Определение 21.6. Функция f называется н е п р е р ы в н о й в т о ч к е a, если бесконечно малому приращению аргумента в точке a соответствует бесконечно малое приращение функции f в точке a, т. е. f(a) ! 0 при x ! 0.

Определение 21.7. Функция f, непрерывная в каждой точке некоторого множества X, называется н е п р е р ы в н о й н а м н о ж е с т в е X. Непрерывность в граничной точке множества X понимается как непрерывность соответственно слева или справа. Если при этом X = D(f), то функцию называют н е п р е р ы в н о й.

21.2.Непрерывность основных элементарных функций

Степенная функция f(x) = xn, где n 2 N, непрерывная функция.

Область определения функции D(f) = R. Дадим аргументу приращение x и рассмотрим приращение функции в некоторой произвольной точке a 2 D(f):

f(a) = f(a + x) f(a) = (a + x)n an = an + nan 1 x + : : : + xn an:

Поскольку при x ! 0 конечная сумма nan 1 x + : : : + xn есть бесконечно малая, то f(a) ! 0 при x ! 0. Согласно определению 21.6 функция f(x) непрерывна в точке a.

В силу произвольности точки a функция f(x) = xn, где n 2 N, непрерывна в своей области опредедения.

Фукции f(x) = sin x, f(x) = cos x непрерывные.

Начнем с функции f(x) = sin x. Область определения функции D(f) = R.

Дадим аргументу приращение x и рассмотрим приращение функции в некоторой произвольной точке a 2 D(f):

В силу ограниченности косинуса и неравенства j sin xj j xj, доказанного в лек-

Поэтому согласно теореме о "двух милиционерах\ f(a) ! 0 ïðè x ! 0, ÷òî доказывает непрерывность синуса.

Д/З: Аналогично доказать непрерывность косинуса.

Показательная функция f(x) = ax, a > 0, a 6= 1, непрерывная функция.

1.Рассмотрим сначала поведение показательной функции в точке x = 0. Доказав,

÷òî

lim ax = a0 = 1;

x!0

докажем тем самым непрерывность показательной функции в точке 0. Очевидно, что 0 предельная точка D(f) = R, 0 2 D(f).

a) Пусть a > 1.

Ранее было доказано1, ÷òî

= n < x < n =

в силу возрастания показательной функции при a > 1 справедливы неравенства

1 " < a 1=n < ax < a1=n < 1 + ":

Таким образом, для каждого " > 0 существует такое число , зависящее от n, а в конечном счете зависящее от ", что при всех x, удовлетворяющих условию

jx aj < , справедливо неравенство jax 1j < ", ò. å. lim ax = 1. Согласно

x!0

определениям 21.1, 21.2 показательная функция f(x) = ax при a > 1 непрерывна в точке 0.

x!0

Непрерывность функции f(x) = ax, a > 0, a 6= 1, в точке 0 доказана.

2.Теперь докажем непрерывность показательной функции в произвольной точ- ке x0 области определения, отличной от 0.

Дадим аргументу приращение x и рассмотрим приращение функции в точ- ке x0:

f(x0) = f(x0 + x) f(x0) = ax0+ x ax0 = ax0 a x 1 :

Òàê êàê ax0 величина ограниченная, а a x 1 ! 0 ïðè x ! 0, òî

lim f(x0) = 0:

x!0

Cогласно определению 21.6 функция f(x) = ax непрерывна в точке x0. Непрерывность показательной функции доказана.

Очевидно, постоянная функция f(x) = c, где c некоторая константа, является непрерывной функцией.

1См. практику 9.

1.Обратная функция2 x = f 1(y) существует на отрезке [c; d], если функция y = f(x) является взаимно-однозначной на [a; b]. Докажем, что строго возрастающая на отрезке [a; b] функция является взаимно-однозначной, т. е. каждое y 2 [c; d] соответствует единственному элементу x 2 [a; b].

Предположим, что существует

y 2 [c; d] : f(x1) = y; f(x2) = y; x1 < x2;

но это противоречит условию строгого возрастания функции f. Следовательно, строго возрастающая на отрезке [a; b] функция y = f(x) является взаимно-однозначной, а это означает, что существует обратная ей функция x = f 1(y).

2. Возьмем произвольные значения y1; y2 2 [c; d] так, чтобы выполнялось неравенство y1 < y2. По свойству взаимно-обратных функций y1 = f (f 1(y1)), y2 = f (f 1(y2)).

Значения строго возрастающей функции f находятся в том же соотношении, что и ее аргументы, следовательно, f 1(y1) < f 1(y2). Это означает, что функция f 1(y) строго возрастает.

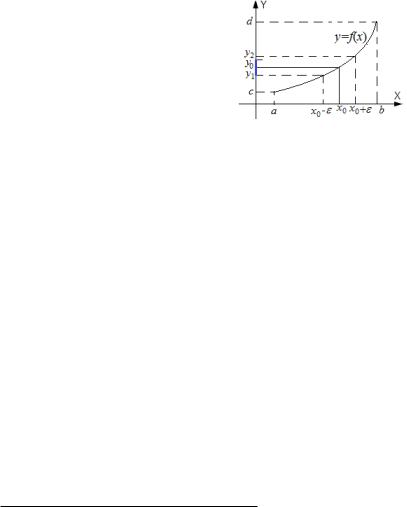
3.Зафиксируем точку y0 2 (c; d) и докажем непрерывность функции f 1(y) в этой точ- ке. Пусть x0 та точка интервала (a; b), в которой f(x0) = y0. Возьм¼м произвольное положительное число " такое, что "-окрестность точки x0 принадлежит интервалу (a; b). Тогда точки y1 = f(x0 ") è y2 = f(x0 + ") попадают в интервал (c; d).

Рис. 2: Взаимно-однозначное соответствие интервалов (x0 "; x0 + ") è (y1; y2).

В силу строгого возрастания функция f(x) устанавливает взаимно-однозначное соответствие интервала (x0 "; x0 + ") на оси OX и интервала (y1; y2) íà îñè OY .

Возьм¼м положительное число такое, что -окрестность точки y0 принадлежит (y1; y2). Тогда вся -окрестность точки y0 при отображении x = f 1(y) попад¼т в "-окрестность точки x0. А это означает непрерывность функции f 1 в точке y0.

При доказательстве односторонней непрерывности функции f 1(y) в концах отрезка c и d рассуждения аналогичны. Нужно только брать соответствующие односторонние окрестности.

Теорема доказана.

Замечание 21.1. Если функция f строго возрастает и непрерывна на интервале (a; b),

Следствие 21.5.2. Функции y = loga x, y = arcsin x, y = arccos x, y = arctg x, y = arcctg x

являются непрерывными.

2См. лекцию 4.