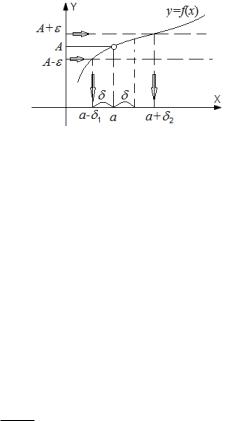
Лекция 19. Предел функции по Коши; критерий Коши существования предела функции в точке

19.1.Определение предела функции по Коши

Определение 19.1. Число A называется пределом функции f в точке a п о К о ш и, если

1.a предельная точка области определения функции f;

2.для каждого " > 0 существует такое число = (") > 0, что при всех x 6= a, удовлетворяющих условию jx aj < , справедливо неравенство jf(x) Aj < ", короче,

8 " > 0 9 (") > 0 : 8 x 0 < jx aj < ) jf(x) Aj < ":

В этом случае пишут

Графически существование предела A функции f в точке a означает следующее. По заданному положительному " строится полоса, параллельная оси Ox, заключ¼нная между прямыми y = A + " и y = A ". Требуется, чтобы существовало такое число > 0, что для всех x из проколотой -окрестности точки a точки графика функции f(x) лежали бы в указанной полосе.

Рис. 1: Иллюстрация определения по Коши предела функции f в точке x = a .

Íà рисунке 1 графически задана некоторая функция f(x), не определенная в точке a, но имеющая предел в этой точке, поскольку

1. a предельная точка области определения функции f;

Вывод: x = 3 предельная точка области определения функции x

p

8 " > 0 9 (") = 9 + " 3 > 0 : 8 x 0 < jx 3j < ) jx2 9j < ":

Согласно определению Коши это означает, что lim x2 = 9:

x!3

1

2.для каждого " > 0 существует такое число (") > 0, что для любой пары точек x0 è x00 из проколотой -окрестности точки a выполняется неравенство jf(x0) f(x00)j < ", короче,

8 " > 0 9 (") > 0 : 8 x0; x00 0 < jx0 aj < ; 0 < jx00 aj < ) jf(x0) f(x00)j < ":

Теорема 19.3.1. (Критерий Коши). Для того чтобы функция f имела в некоторой точ- ке конечный предел, необходимо и достаточно выполнения для f в этой точке условия Коши.

Таким образом, необходимость условия Коши установлена. Достаточность. Пусть теперь выполнено условие Коши:

8 " > 0 9 (") > 0 : 8 x0; x00 0 < jx0 aj < ; 0 < jx00 aj < ) jf(x0) f(x00)j < ":

Рассмотрим произвольную последовательность точек fxng из области определения функции f такую, что xn ! a ïðè n ! 1 è xn 6= a для всех n. Тогда существует число N, зависящее от , а в конечном сч¼те зависящее от ", такое, что при всех n > N для точек xn справедливо неравенство jxn aj < .

Значит, если натуральные числа n и m превосходят N, то jf(xn) f(xm)j < " и для последовательности ff(xn)g выполняется условие Коши (ff(xn)g фундаментальная).

Итак, для любой такой последовательности точек fxng существует конечный предел последовательности ff(xn)g. Согласно теореме2 18.1.1 функция f имеет предел в точке a. Теорема доказана.

Пример 19.2. Доказать, используя критерий Коши, что функция

имеет lim f(x):

x!0

Заметим, что x = 0 предельная точка D(f). Очевидно, что для каждого " > 0 и любых x0, x00 из проколотой окрестности точки x = 0 выполняется f(x0) = 1, f(x00) = 1 è jf(x0) f(x00)j = 0 < ". Таким образом, функция f удовлетворяет условию Коши в точке x = 0, следовательно, согласно критерию Коши имеет конечный предел в этой точке.

2Функция имеет предел в точке a тогда и только тогда, когда на любой последовательности точек

fxng из ее области определения, сходящихся к a и отличных от a, последовательность соответствующих значений функции ff(xn)g сходится.

19.4.Предел функции на бесконечности

Определение 19.3. Число A называется пределом функции f при x ! 1 п о Г е й н е, если

1. существует число L > 0 такое, что функция f определена при всех jxj > L;

2. для каждой последовательности fxng, все числа xn которой принадлежат области

определения функции f и xn ! 1, справедливо равенство A = lim f(xn).

n!1

Определение 19.4. Число A называется пределом функции f при x ! 1 п о К о ш и, если

1.существует число L > 0 такое, что функция f определена при всех jxj > L;

2.для каждого " > 0 существует такое число (") > 0, что при всех jxj > выполняется неравенство jf(x) Aj < ".

Рис. 2: Иллюстрация определения по Коши предела функции f на бесконечности.

Íà рисунке 2 графически задана некоторая функция f(x), имеющая предел равный числу A при x ! 1, поскольку

Определения пределов при x ! +1 (x ! 1) аналогичны.

Определение 19.5. Число A называется пределом функции f при x ! +1 (x ! 1)

ïî Ã å é í å, åñëè

1.существует число L такое, что функция f определена при всех x > L (x < L);

2.для каждой последовательности fxng, все числа xn которой принадлежат области определения функции f и xn ! +1 (xn ! 1), справедливо равенство

A = lim f(xn):

n!1

Определение 19.6. Число A называется пределом функции f при x ! +1 (x ! 1)

ïî Ê î ø è, åñëè

1.существует число L такое, что функция f определена при всех x > L (x < L);

2.для каждого " > 0 существует такое число (") > 0, что при всех x > (x < ) выполняется неравенство jf(x) Aj < ".

Д/З: Эквивалентность приведенных определений по Гейне и по Коши доказывается аналогично теореме 19.2.1; критерий Коши существования предела функции на бесконечности формулируется и доказывается аналогично тому, как это было сделано в пункте 19.3.. Проделать все это самостоятельно.

19.5.Бесконечный предел

Дадим определения случаям, когда пределом является не число, а бесконечность.

Определение 19.7. (п о К о ш и) Говорят, что предел функции f в точке a равен беско-

нечности, и пишут

lim f(x) = 1;

x!a

åñëè

1.a предельная точка области определения функции f;

2.для каждого E > 0 существует такое число (") > 0, что при всех x, удовлетворяющих условию 0 < jx aj < , выполняется неравенство jf(x)j > E.

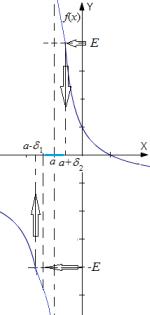
Рис. 3: Иллюстрация определения по Коши бесконечного предела функции f в точке a.

Íà рисунке 3 графически задана некоторая функция f(x), не определенная в точке a, но имеющая в этой точке бесконечный предел, поскольку

Определение 19.8. (п о К о ш и) Говорят, что предел функции f при x ! 1 равен

бесконечности, и пишут

lim f(x) = 1;

x!1

åñëè

1.существует число L > 0 такое, что функция f определена при всех jxj > L;

2.для каждого E > 0 существует такое число (") > 0, что при всех x, удовлетворяющих условию jxj > , выполняется неравенство jf(x)j > E.