75. Пуассон теңдеуі үшін Дирихле айырымдылық есебін шешудің орнықтылық айқын әдісі. Жинақтылық шарты қарапайым екі қабатты ауыспалы бағыттар схемасы.

Шекарасы 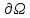болатыноблысында(1) есебін қарастырамыз.облысының аппроксимациясындеп, ал шекарасыоблысының аппроксимациясын

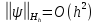деп белгілейік. (2) Аппроксимациясы. Айталық (1) есебінің шешімінің шектелген төртінші ретті туындысы бар болсын. Онда, Тейлор қатарына жіктей отырып, алатынымыз Сондықтаншешімі үшін алатынымызяғниторынданемесе. Сонымен, (2) айырымдылық есебі (1) Дирихле есебінбойынша екінші ретпен аппроксимациялайды.

Орнықтылығы. кеңістігіндеторында анықталған функциясының нормасын анықтайық. Бұл нормакеңістігінде анықталған норма. Енді (2) схемасының орнықтылығын дәлелдеу үшін, алдымен, осы орнықтылықтың анықтамасымен бірге кез келген оң жағымен шекаралық шартыүшін (2) есебінің шешімі жал,ыз болатынын көрсетейік, яғни, мұндағы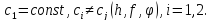(3)Лемма 1. Айталық функциясыторында анықталған және барлық ішкінүктелерінде(4) шартын қанағаттандырсын .ондафункциясыторында өзінің ең үлкен мәніншекарасының әйтеурі бір нүктесінде қабылдайды.

Дәлелдеуі: кері жорыйық торынанфункциясы өзінің ең үлкен мәнін қабылдайтын және ең үлкен абсциссалынүктесін алайық. Онда, біздің ұйғарым бойыншаішкі нүктесі жәнеендешенүктесінде

себебі алымындағы бірінші жақша теріс,ал қалған жақшалар оң емес. Бұл(4)-ші шартқа қарама қайшы. Лемма 1 дәлелденді.

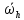Лемма 2. Айталық функциясыторында анықталған және барлық ішкінүктелерінде(5) шартын қанағаттандырсын .ондафункциясыторында өзінің ең кіші мәніншекарасының әйтеурі бір нүктесінде қабылдайды.

Дәлелдеуі: . Лемма 1 сияқты дәлелденеді.

Теорема (Максимум принципі).

(6) айырымдылық теңдеуінің әрбір шешімі өзінің ең үлкен және ең кіші мәндеріне шекарасының әйтеуір бір нүктесінде жетеді.

Дәлелдеуі: Лемма 1 мен Лемма 2-нің тұжырымдарын біріктіруден шығады. Максимум принципінен шығатыны

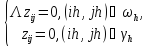(7)

Есебінің тек қана нолдік шешімі болады, себебі осы шешімі ең үлкен және ең кіші мәндеріншекарасында қабылдайды, ал шекарасындасондықтан да(2)-ші сызықты теңдеулер жүйесінң анықтауышы нолден өзгеше және (2) шекаралық есебінің (оң жағы және шекаралық шартымен) бір ғана шешімі, кез келген оң жағы және шекаралық шарты болады. Енді (3) бағасын дәлелдейік. Ʌz

формуласынан кез келген екінші дәрежелі көпмүшелік

P(x,y)=a үшін

(8)

теңдігі орындалады.(2) өрнектерінің оң жақтарыжәне функцияларын пайдаланып және R деп алып, көмекші функциясын құрамыз. Бұл функцияны тек қана торында қарастырамыз. (8) формуланың күшімен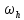торыныңбарлық нүктелерінде.

Сондықтан да (2) есебінің шешімі –пен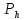функцияларының айырымыторының нүктелеріндетеңсіздігін қанағаттандырады. Лемма 1-дің

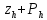нәтижесінен айырымы өзінің ең үлкен мәніншекарасында қабылдайды. Ал осышекарасында бұл айырымоң емес, себебібірлік квадратындажәне оң жағындағы екі тік жақшалары оң емес. Бұдан,айырымының ең үлкен мәні оң емес, онда барлық-та ,немесе ,. Тура осы сияқты ,функциясы үшінторының барлық нүктелерінде

ал шекарасындақосындысы теріс емес. Онда Лемма 2-дің нәтижесіненқосындысы-тың барлық нүктелерінде теріс емес, яғнинемесе -. Сонымен-тың барлық нүктелерінде

мұндағы c=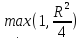яғни (3) бағасыболғанда алынады. Теорема толық дәлелденді.