
- •66. Сызықтық алгебралық теңдеулер жуйесін (сатж) шешудің дәл және итерациялық әдістері. Квадрат түбірлер әдісі. Халецкий әдісі. Итерация және Зейдель әдістері
- •1.Квадрат түбірлер әдісі.
- •2.Халецкий әдісі.
- •3.Итерация әдісі.
- •67. Матрицаның модулі бойынша ең үлкен меншікті мәнін және соған сәйкес меншікті векторын табу. Итерациялық әдістері
- •68. Сызықтық емес және трансценденттік теңдеулерді шешудің итерациялық әдістері. Қиюшылар, Ньютон және итерация әдістері
- •69.Функцияны интерполяциялау. Лагранж, Ньютон және Гаусстың интерполяциялық формулалары. Қалдық мүшелері
- •70. Сандық интералдау. Ньютон-Котестің квадратуралық формуласы. Симпсон формуласы жане оның қалдық мүшесі.
- •71. Нормаланған кеңістіктің аппроксимациясы. Ішкі және сыртқы аппроксимациялары. Дифференциалдық операторлардың аппроксимациялары.
- •72. Екінші ретті қарапайым дифференциалдық теңдеулер үшін шекаралық есебін шешудің қуалау әдісі
- •73. Жылуөткізгіштік теңдеуінің айқындалған, айқындалмаған схемалары және салмақтары бар схемалары. Аппроксимация реті және орнықтылығы. Жинақтылығы.
- •74. Тербеліс теңдеуінің салмақтары бар айырымдылық схемалары. Аппроксимация реті және орнықтылығы. Жинақтылығы.
- •75. Пуассон теңдеуі үшін Дирихле айырымдылық есебін шешудің орнықтылық айқын әдісі. Жинақтылық шарты қарапайым екі қабатты ауыспалы бағыттар схемасы.
66. Сызықтық алгебралық теңдеулер жуйесін (сатж) шешудің дәл және итерациялық әдістері. Квадрат түбірлер әдісі. Халецкий әдісі. Итерация және Зейдель әдістері
САТЖ шешу әдістерін негізгі екі топқа бөлуге болады:
1.Дәл әдістері-жүйе шешімін есептеудің ақырлы алгоритмдерін береді (Крамер, Гаусс, негізгі элементтер, квадрат түбірлер т.б. әдістері).
2.Итерациялық әдістер-берілген дәлдікпен жинақталатын шексіз процесстер арқылы жүйе шешімін алуға мүмкіндік береді (итерация,Зейдель,релаксация т.б. әдістері).Дөңгелектеу нәтижесінде дәл әдістердің де нәтижелері жуық болуы мүмкін ,оның үстіне,жалпы жағдайда,түбір қателігінің бағасын алу қиындық тудырады. Ал итерациялық процесстерді қолданғанда тағы әдіс қателігі қосылады.Итерациялық әдістерді тиімді пайдалану бастапқы жуықтауды таңдауға және процесс жинақтылығының тездігіне байланысты.
1.Квадрат түбірлер әдісі.
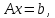 (1)
(1)
мұндағы
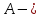 симметриялы
матрица, яғни
симметриялы
матрица, яғни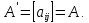
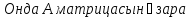 транспонирленген
екі үшбұрышты матрицаның көбейтіндісі
түрінде алуға болады.
транспонирленген
екі үшбұрышты матрицаның көбейтіндісі
түрінде алуға болады.
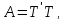 (2)
(2)
мұндағы
 және
және .
.


 матрицасының
матрицасының
 элементтерін анықтау үшін
элементтерін анықтау үшін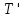 және
және матрицаларын көбейтіп келесі теңдеулерін
аламыз:
матрицаларын көбейтіп келесі теңдеулерін
аламыз:
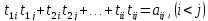



Табамыз:
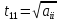 ,
,
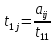 (j>1)
(j>1)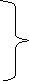
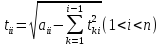 (3)
(3)

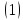 жүйенің
анықталған бір ғана шешімі болады,егер
жүйенің
анықталған бір ғана шешімі болады,егер
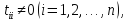 онда
онда
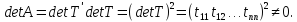
 матрицасының
коэффициенттері нақты болады,егер
матрицасының
коэффициенттері нақты болады,егер
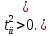 Бірақ
міндетті түрде емес). (2) орындалғанда
(1) теңдеуі мына екі теңдеуге эквивалент:
Бірақ
міндетті түрде емес). (2) орындалғанда
(1) теңдеуі мына екі теңдеуге эквивалент: немесе ашып жазсақ,
немесе ашып жазсақ,


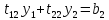

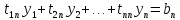 (4)
(4)
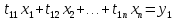


… … … … … … …
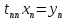 (5)
(5)
Осылардан біртіндеп табамыз:
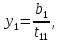

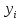 =
=
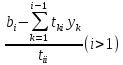 (6)
(6)
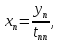
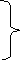
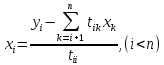 (7)
(7)
2.Халецкий әдісі.
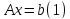

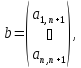
 матрицасын
төменгі үшбұрышты матрица
матрицасын
төменгі үшбұрышты матрица
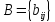 мен диагоналі бірлерден тұратын жоғарғы
үшбұрышты матрицасының
мен диагоналі бірлерден тұратын жоғарғы
үшбұрышты матрицасының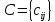 көбейтіндісі ретінде қарауға болады,
яғни
көбейтіндісі ретінде қарауға болады,
яғни
 (2)
(2)
мұндағы



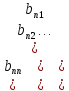

Онда
 және
және
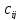 элементтері келесі формулалармен
анықталады:
элементтері келесі формулалармен
анықталады: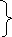
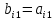 ,
,
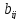 =
=
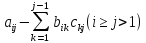 (3)
(3)


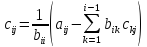 (
(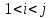 )
(4)
)
(4)
Бұдан
ізделінді
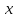 векторын
векторын
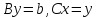 (5)
(5)
теңдеулерді
біртіндеп шешу арқылы табуға болады.
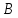 және
және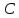 матрицалары үшбұрышты болғандықтын,
(5) жүйелері оңай шешіледі, яғни
матрицалары үшбұрышты болғандықтын,
(5) жүйелері оңай шешіледі, яғни
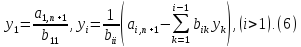
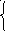

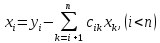 (7)
(7)
(6)
формуласынан
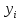 белгісіздерді
белгісіздерді коэффициенттерімен бірге есептеген
ыңғайлы екені көрінеді.
коэффициенттерімен бірге есептеген
ыңғайлы екені көрінеді.
Егер
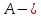 симметриялы
болса,яғни
симметриялы
болса,яғни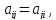 онда
онда (
( ).
).
3.Итерация әдісі.
 ,
,
 ,
, ,
,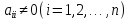 деп
жорып, (1)
жүйенің
бірінші теңдеуін
деп
жорып, (1)
жүйенің
бірінші теңдеуін
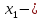 ге
қатысты, екіншісін
ге
қатысты, екіншісін ге
қатысты және т.с.с. шешейік. Нәтижесінде
келесі эквивалент жүйесін аламыз:
ге
қатысты және т.с.с. шешейік. Нәтижесінде
келесі эквивалент жүйесін аламыз: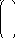
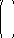

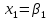 +
+
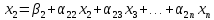
… … … … … … … (2)
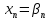 +
+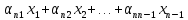
мұндағы
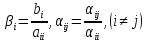 және
және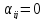 егер
егер
 ,
,
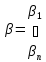 арқылы
жүйесін мына түрде жазайық :
арқылы
жүйесін мына түрде жазайық :

 (2’)
(2’)
(2’)
жүйесін
біртіндеп жуықтау әдісімен шешеміз.
Нөлдік жуықтау ретінде
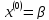 аламыз. Ары қарай,
аламыз. Ары қарай, және т.с.с.
және т.с.с. (
(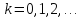 )
(3)
)
(3)
Егер
 ,
,

 болса,онда
бұл шек
болса,онда
бұл шек жүйенің шешімі болады. Шынында да ,
жүйенің шешімі болады. Шынында да , теңдеуінде шекке көшсек :
теңдеуінде шекке көшсек : =
=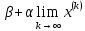 немесе
немесе
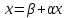 ,яғни
,яғни
 шектік
элемент
шектік
элемент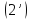 шешімі болады,онда ол
шешімі болады,онда ол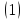 жүйенің де шешімі.
жүйенің де шешімі.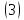 теңдеулерін ашып жазсақ,
теңдеулерін ашып жазсақ,

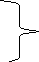
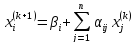 ,
(3’)
,
(3’)
(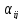 =0,
=0, )
)
 орындалу
үшін
орындалу
үшін
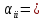
 +
+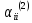 деп алу керек, мұндағы
деп алу керек, мұндағы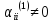 .
Онда (1) жүйеден
.
Онда (1) жүйеден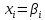 +
+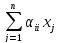
 мұндағы
мұндағы
 ,
, және (3’)итерация
әдісі
деп аталады.
және (3’)итерация
әдісі
деп аталады.
4.Зейдель
әдісі. Айталық
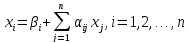 жүйесі берілсін. Кез-келген
жүйесі берілсін. Кез-келген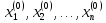 жуықтауларын
алдық делік. Енді түбірлерініңk–шы
жуықтаулары
жуықтауларын
алдық делік. Енді түбірлерініңk–шы
жуықтаулары
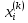 белгілі деп түбірлерініңk+1
–ші жуықтауларын келесі формуласымен
есептейміз:
белгілі деп түбірлерініңk+1
–ші жуықтауларын келесі формуласымен
есептейміз:


… … … … … … …
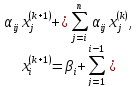
… … … … … … …


Зейдель әдісі,қарапайым итерация әдісіне қарағанда, жақсы (тез) жинақтылықты береді. Бірақ-та өте көп есептеулерді қажет етеді.Қарапайым итерация әдісі жинақталмаған жағдайларда да Зейдель әдісі жинақталуы мүмкін. Зейдель әдісінің қарапайым итерация жайырақ жинақталатын кездері де болады. Тіпті,қарапайым әдісі жинақталып, Зейдель әдісі жинақталмайтын жағдайлар болады.
