
GOS / 10_surak_dismat
.docx10. ПІКІРЛЕР ЛОГИКАСЫНЫҢ ФОРМУЛАЛАРЫ. ФОРМУЛАЛАРДЫҢ АҚИҚАТТЫҚ МӘНДЕРІ. ФОРМУЛАЛАРДЫҢ АҚИҚАТТЫҚ КЕСТЕСІ. ПІКІРЛЕР ЛОГИКАСЫНДАҒЫ ДЕДУКЦИЯ ТУРАЛЫ ТЕОРЕМА.
Анықтама.
Пікірлер
логикасының тілі
алфавиттен
– L,
логикалық операциялардан – Log,
қосымша символдардан – D
тұрады. 1
арқылы
әріптер жиынын белгілейміз. Әріптер
латын алфавитінің бас әріптері арқылы
жазылады –A ,B,C қажет болған жағдайда
индекстерді қолдануымызға болады: A 1
, B12,
Ci
және т.с.с. Сонымен L=
1
арқылы
әріптер жиынын белгілейміз. Әріптер
латын алфавитінің бас әріптері арқылы
жазылады –A ,B,C қажет болған жағдайда
индекстерді қолдануымызға болады: A 1
, B12,
Ci
және т.с.с. Сонымен L=
 .
.
Log={ ˄ немесе & (коньюнкция), ˅(дизьюнкция), →(импликация),
¬(терістеу), ↔(эквиваленттілік)– логикалық амалдар жиыны.
D={ ( (сол жақша), ) (оң жақша), , (үтір) }– қосымша символдар жиыны.
Анықтама.Әріптердің, логикалық амалдардың және қосымша символдардың кез келген шектелген тізбегін сөз деп атаймыз. Егер α=Δα=αΔ теңдігі орындалса, онда Δ сөзі бос сөз деп аталады және бұл сөз ешбір символдан тұрмайды деп есептейміз. Ал α және β сөздері үшін α=γβτ болатындай γ және τ сөздері табылса, β сөзі α сөзінің ішкі сөзі деп аталады. Β=τ=Δ мүмкіндігі сақталғандықтан, әр сөз өзінің ішкі сөзі болады. Әрбір тілдегідей, алфавит символдарынан құрылған сөздердің мағыналысы да мағынасызы да кездесуі мүмкін. Мағыналы сөздер біздің пәніміздің негізгі зерттеу нысандарын құрады. Оларды пікір деп атаймыз. Осы пікір ұғымының дәл анықтамасын берейік. Анықтама. Ақиқат немесе жалған мәндердің бірін ғана қабылдайтын хабарлас сөйлемді пікір деп атаймыз. Пікірлерді Σ1 жиынынан алынған әріптермен белгілейміз. Мысалы, “Бүгін күн жылы” хабарлас сөйлемі пікір болмайды, себебі бұл сөйлемнің ақиқат немесе жалған болатынын анықтау үшін оқиғаның уақыты пен ӛтетін орны белгілі болуы керек. Ал “Алматыда 2008 жылдың 10 шілдесінде күн ашық және ыстық болды“ сөйлемінің ақиқат немесе жалған екендігіне әрқашан көз жеткізуімізге болады. Енді қарапайым пікірлерден күрделі пікірлерді, яғни пәніміздің мағыналы сӛйлемдерін (формулаларды) алу тәртібін көрсететін анықтаманы берейік.
Анықтама.
1. Әрбір әріп формула болады.
2. Егер φ,ψ формулалар болса, онда ¬φ, (φ˄ψ), (φ ˅ψ), (φ →ψ) және сөздері де формулалар болады.
3. Кез келген формула 1-ші және 2-ші ережелерді ақарлы рет қолдану арқылы ғана құрылады.
Формулаларды кіші грек әріптерімен:φ,ψ,θ, … белгілейміз. Мысал. Төмендегі өрнектер пікірлер логикасының сөздері болады.
-
(A1→¬A3) ˄ A→A1
-
(¬A4→)
-
¬((A2 ˅¬A2)→A1)
Мұндағы алғашқы екі сөз формула болмайды, ал үшіншісі пікірлер логикасының формуласы. Формуланың анықтамасы – олардың құрылуы бойынша индукциялық анықтама, сондықтан бұл анықтама формулалардың қасиеттерін формуланың күрделілігі бойынша индукцияны қолдану жолымен дәлелеуге мүмкіндік береді
Келісім: Формуладағы жақшалар санын кеміту мақсатымен, логикалық амалдардың орындалу реттерін тағайындайық. Алдымен ¬(терістеу), екінші кезекте ˄ (коньюкция) және ˅ (дизьюнкция), үшінші кезекте→ (импликация), ең соңынан ↔(эквиваленттілік) орындалады деп келіселік.
Анықтама.Өзі де формула болатын берілген формуланың ішкі сөзін ішкі формула дейміз.
Енді формулалардың мағынасына көңіл аударалық. Әрбір пікір не ақиқат, не жалған мән қабылдауға тиіс. Ал кез келген формуланың ақиқаттық мәні – құрамындағы қарапайым пікірлердің ақиқаттық мәндерімен толық анықталады. Сондықтан формулалардың ақиқаттық мәнін анықтау үшін, алдымен ақиқаттық функция ұғымын енгіземіз.
Анықтама. A1,… An әріптері берілсін. Кез келген ν : { A1,… An }→ {а ,ж } функциясыақиқаттық функция деп аталады. A1,… An әріптерінің функциясы бойынша бейнелерінің тізбегін ақиқаттық мәндердің орналасуы деп айтамыз.
Төмендегі индукциялық анықтама – ақиқаттық ұғымын бүкіл пікірлер логикасының формулалар жиынына ұлғайтуға мүмкіндік береді.
Анықтама. φ формуласында кездесетін әріптер A1,… Anболғанда, кез келген
ν : { A1,… An } →{ а,ж } функциясын ақиқаттық функция (немесе интерпретация) деп
айттық.
Осы функцияға сәйкес формуласының
ақиқаттық мәнін (Белгілеуі:
 )
келесі
)
келесі
тәртіппен анықтаймыз.
1.φ=
A1болса,
онда
 (φ
)=
(φ
)=
 (A1)
(A1)
2. Егер
φ=ψ˄θ
, онда
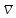 (φ
) = а⇔
(φ
) = а⇔ (ψ
)және
(ψ
)және
 (φ
)= а
(φ
)= а
3. Егер
φ=¬ψ
болса, онда
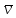 (φ
)= а⇔
(φ
)= а⇔ (ψ
)= ж
(ψ
)= ж
4. Егер
φ=ψ
˅θ
, онда
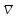 (φ
)=ж⟺
(φ
)=ж⟺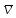 (ψ
) = ж
немесе
(ψ
) = ж
немесе
 (φ)=
ж
(φ)=
ж
5. Егер
φ=ψ→θ
, онда
 (φ
)= ж⇔
(φ
)= ж⇔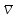 (ψ
) = а
және
(ψ
) = а
және
 (θ
) = ж
(θ
) = ж
Осы анықтаманы төмендегідей кестеге жинақтауға болады.
|
А |
В |
¬ А |
А˄В |
А ˅В |
А→В |
|
а |
а |
ж |
А |
а |
А |
|
а |
ж |
ж |
Ж |
а |
Ж |
|
ж |
а |
а |
Ж |
а |
А |
|
ж |
ж |
а |
Ж |
ж |
А |
Мысал ((¬(А˄¬В) ˄В)→А) формуласының ақиқаттық кестесін құрайық
|
А |
В |
(А˄¬ В |
¬(А˄¬В |
¬(А ˄¬В) ˄В |
(¬(А˄¬В) ˄В)→А |
|
а |
а |
Ж |
А |
А |
А |
|
а |
ж |
А |
Ж |
Ж |
А |
|
ж |
а |
Ж |
а |
А |
Ж |
|
ж |
ж |
Ж |
ж |
Ж |
А |
Көпшілік жағдайда формуланың ақиқаттық мәнін ақиқаттық кестені құрмай, төмендегі ережелерді пайдаланып анықтау тиімді.
І. Коньюнкция ережеcі. Коньюнкция ақиқат болуы үшін, ондағы әрбір коньюнкция мүшесі (конъюнкт ) ақиқат болуы қажетті және жеткілікті.
ІІ. Дизьюнкция ережесі. Дизьюнкция жалған болуы үшін, ондағы әрбір дизьюнкция мүшесі (дизъюнкт) жалған болуы қажетті және жеткілікті.
φ=ψ→θ импликациясындағы ψ формуласы импликацияның себебі, ал θ формуласы салдары деп аталады.
ІІІ. Импликация ережесі. Импликация жалған болуы үшін оның себебі ақиқат, салдары жалған болуы қажетті және жеткілікті. Бұл ережені басқаша жолмен тағайындауға болады. Импликация ақиқат болуы үшін себебі жалған немесе салдары ақиқат болуы қажетті және жеткілікті. Осы ережелерді пайдаланып, логикалық амалдардың ақиқаттық кестесін қысқаша былай толтыруға болады.
|
А |
В |
¬ А |
А˄В |
А ˅В |
А→В |
|
а |
А |
ж |
а |
|
|
|
а |
Ж |
ж |
|
|
Ж |
|
ж |
А |
|
|
|
|
|
ж |
Ж |
|
|
ж |
|
Мұндағы бос орындар келтірілген ақиқаттық мәндерге қарама-қарсы мәндермен толтырылған деп есептейміз. Келтірілген ақиқаттық кестелердің ішіндегі импликацияның ж →ж= а, ж→ а= а және а →ж= ж нәтижелері дүдәмал кӛрінуі мүмкін.
Дедукция теоремасы. Г формулалар жиыны берілсін. Егер қандай да бір φ және ψ пікірлер есептеулерінің формулалары болса, онда Г, φ⊢ψ⟺Г⊢φ→ψ. Дәлелдеуі. (⇒) : Айталық φ1 , φ2 , ... φn формулалар тізбегі Г⋃ {φ} жынындағы ψ формуласының қорытуы болсын. Онда анықтама бойынша φn = ψ болады. Теореманы дәлелдеуі қорытудағы формулалардың саны бойынша индукцияны пайдаланып жүргізейік.
n=1 болғанда φ1 =ψ . Біз Г⃒‒φ→φ1 қорытуының оррынд алатынын көрсетуіміз керек. Мұндағы φ1 формуласы үшін төменндегі жағдайлардың бірі орындалады.
а) φ1 – аксиома
b) φ1∊ Г⋃{φ } . Онда φ1∊Г немесе φ1 =φ жағдайларының бірі болады.
Егер φ1 =φ болса, онда 3.1 леммасы бойынша ⃒‒φ→φ.Онда қорытудың екінші қасиеті бойынша Г⃒‒φ→φ1 немесе Г⃒‒φ→φ. Демек шарт бойынша Г⃒‒φ→φ1 немесе Г⃒‒φ→ψ.
Ал (а) және (b) пунктінің φ1 ∊Г жағдайлары үшін Г⃒‒φ1 (*) және Г1 аксиома нұсқасы бойынша Г⃒‒φ1→(φ→φ1) (2*). Онда(*) және (2*) қорытуларына МР(қосу ережесі) ережесін қолдансақ ,
Г⃒‒φ→φ1 немесе Г⃒‒φ→ψ .
Енді
кез келген k n
үшін теореманың тұжырымы дұрыс болсын
деп есептейік . Яғни Г⃒‒φ→φk
(3*) қорытуы орындалады.
n
үшін теореманың тұжырымы дұрыс болсын
деп есептейік . Яғни Г⃒‒φ→φk
(3*) қорытуы орындалады.
Енді теореманы φn формуласы үшін дәлелдейміз. Φn =ψ және φn формуласы үшін төмендегі үш жағдайдың бірі орындалады.
а) φn – аксиома
b) φn∊ Г⋃{φ } .
c) φn формуласы φi және φj формулаларынанМР ережесі арқылы алынған.
Алдыңғы екі жағдайды дәлелдеулері n=1 болғандағы дәлелдеулерді қайталайды.
(c)
жағдайын дәлелдейік. i,
j
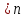 болғандықтан
, индукция жоруы бойынша
болғандықтан
, индукция жоруы бойынша
Г⃒‒φ→φi
және Г⃒‒φ→φj
(1). Егер
i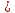 j деп есептесек
жиындағы қорытуға байланысты ескерту
бойынша φi=φj→φnонда
Г⃒‒φ→φj
қорытуының орнына Г⃒‒φ→(φi→φj→φn)
(2 ) қорытуын жазамыз.
j деп есептесек
жиындағы қорытуға байланысты ескерту
бойынша φi=φj→φnонда
Г⃒‒φ→φj
қорытуының орнына Г⃒‒φ→(φi→φj→φn)
(2 ) қорытуын жазамыз.
Ал Г2 аксиомалар нұсқасы бойынша
Г⃒‒(φ→φj)→((φ→(φj→φn)) →(φ→φn))
Қорытуы орындалады.
Бұған (1) және (2) қорытуларын пайдаланып , МР қорытыту ережесін екі рет қолдансақ, Г⃒‒ φ→φn болатынын көреміз. Онда φn ∊ψ болғандықтан, Г⃒‒φ→ψ.
(⇐) енді Г⃒‒φ→ψ болсын деп есептейік. Онда қорытудың 3-ші және 4-ші қасиеттері бойынша Г, φ⃒‒φ және Г, φ⃒‒φ→ψ. Бұл екі қорытуға МР ережесін қолдансақ , Г, φ⃒‒ψ қорытуын аламыз. Теорема дәлелденді.
Лемма 3.1 (cөздер туралы теорема) r әріптен тұратын А={a1 , …ar } алфавитіндегі ұзындығы m-ге тең әртүрлі сөздер саны rm болады.
Пікірлер есептеуінің классикалық аксиомалар жүйесі келесі он аксиомалар нұсқаларынан тұрады.
Г1. φ→(ψ→φ)
Г2. (φ→ψ)→((φ→(ψ→θ))→(φ→θ))
Г3. (φ˄ψ)→φ
Г4. (φ˄ψ)→ψ
Г5. φ→(φ˅ψ)
Г6.ψ→(φ˅ψ)
Г7. (φ→ψ)→((φ→θ)→(φ→(φ˄θ)))
Г8. (φ→θ)→((ψ→θ)→((φ˅ψ)→θ))
Г9. (φ→¬ψ)→(ψ→¬φ)
Г10. ¬¬φ→φ
