69.Функцияны интерполяциялау. Лагранж, Ньютон және Гаусстың интерполяциялық формулалары. Қалдық мүшелері

Ньютонның бірінші интерполяциялық формуласы.

Есептің қойылуы. Айталық y = f(x) функциясының, тәуелсіз айнымалылары бір – бірінен бірдей қашықтықта жатқан x_i = x₀ + ih, i = 0, 1,…, n мәндерінде, h - интерполяция қадамы, мәндер y_i = f(x_i) берілсін. Дәрежесі n - нен аспайтын және x_i нүктелерінде y_i - ге тең болатын, яғни

P_i(x_i) = y_i, i = 1,2,…,n, (1)

oрындалатын P_n(x) полиномын табу (құру) керек.

(1) – ші шарты келесі шартқа эквивалетті

∆^mP_n(x_o) = ∆^my₀, m = 0,1,2,…,n. (2)

Ньютон мырза полиномды келесі түрде іздеген

P_n(x) = a₀ + a₁(x – x₀) + a₂(x – x₀)*(x – x₁) + …+a_n(x – x₀)*…*(x – x_n-1)

Жалпыланған дәрежені қолдансақ,

P_n(x) = a₀ + a₁(x – x₀)^[1] + a₂(x –x₀)^[2]+ … + a_n(x –x₀)^[n] (3)

P_n(x) полиномының a_i (i = 0, 1, …, n) коэффициенттерін анықтайық. Ол үшін x = x₀ деп алып (3) формуладан алатынымыз:

P_n(x₀) = y₀ = a₀.

a₁ коэффициентін анықтау үшін бірінші ақырлы айырымын құрайық.

∆P_n(x) = h*a₁ + 2*h*a₂(x –x₀)^[1] + 3*h*a₃(x – x₀)^[2] + … + n*h*a_n(x – x)^[n-1]

Енді x = x₀ деп алып, табатынымыз: ∆P_n(x₀) = ∆y₀ = a₁h→ a₁ = . a₂ - ні табу үшін екінші ақырлы айырымын құрамыз, яғни ∆²P_n(x) – ті есептейміз:

∆²P_n(x) = 2!*h²*a₂ + 2*3*h²*a₃(x –x₀)^[1] + … + (n – 1)*n*a_n(x – x)^[n-2]

Енді x = x₀ деп алып, табатынымыз: ∆²P_n(x₀) = ∆²y₀ = 2!*h²*a₂ → a₂ = Осы процесті жалғастыра отырып, a_i ( i = 0,1,2,…,n) барлығын табамыз, a_i = ( i = 0,1,2,…,n),мұнда 0! = 1, ∆⁰y = y.

a_i kоэффициенттерін (3) формулаға қойып, Ньютонның бірінші интерполяциялық полиномын аламыз

P_n(x) = y₀ + (x –x₀)^[1] + (x – x₀)^[2] + … + (x – x₀)^[n] (4)

Осы полином қойылған талаптың барлығына да сәйкес келеді. Расында да, 1) P_n(x) - тің дәрежесі n – нен аспайды, 2) P_n(x) = y₀ және P_n(x_k) = (1 + ∆)^ky₀ = y_k (k = 1,2,…,n) . Соңғы тұжырымды өздеріңіз дәлелдеңіз.

h→o - да байқайтынымыз = ()_x=x0 = y^(k)(x₀) және ^[n] = (x – x₀)ⁿ . Осыларды ескере отырып, (4) – тен алатынымыз P_n(x) = y(x₀) + y’(x₀)(x – x₀) + … +(x – x₀)ⁿ – Тейлор полиномы.

Іс жүзінде немесе жеке комрьютерде есеп шығарғанда, Ньютонның келесі, бірінші полиномын пайдаланамыз. Ол үшін, алдымен

q – жаңа айнымалысын енгіземіз. Ендеше= q(q – 1)(q – 2) … (q – I + 1), (i = 1,2,…,n) . Бұдан,

P_n(x) = y₀ + q∆y₀ + ∆²y₀ + … + 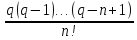∆ⁿy₀, (5)

Мұндағы q = нүктесінен бастап х нүктесіне жету үшін қажетті қадамдар саны. (5) формуласы Ньютонның бірінші немесе алға формуласы деп аталады. Бұл формуланы y = f(x) функциясын x₀ нүктесіне жақын маңайда қолданған жөн. Мұндағы q модулі бойынша өте аз шама.

Ньютонның екінші интерполяциялық формуласы.

Есептің қойылуы өзгермейді, яғни Ньютонның бірінші интерполяциялық формуласы сияқты формула табу керек. Мұнда да x_i = x_o + ih, i = 0,1, …,n деп аламыз да, интерполяциялық полиномды келесі түрде іздейміз

P_n(x) = a₀ + a₁(x – x_n) + a₂(x – x_n)(x – x_n-1) + … +a_n(x – x_n)(x – x_n-1)…(x – x₁).

Белгісіз коэффициенттері a_i – лерді табу үшін біз Ньютонның бірінші формуласындағы x₀ – ді x_n - ге ауыстырып, барлық амалдарды орындаймыз. Сонда алатынымыз:

P_n(x_n) = y_n = a₀, a₁ = 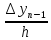, …, a_i = , i = 0,1,2,…,n. Бұдан шығатыны

P_n(x_n) = y_n + (x – x_n) + (x – x_n)(x – x_n-1) + …+ (x – x_n)…(x –x₁).

Немесе q = десек, онда

= =q +1, 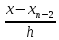= q + 2 т.с.с. соңғы формуладан алатынымыз:

P_n(x) = y_n + q∆ⁿy_n-1 + ∆²y_n-2 + … + ∆ⁿy_o. Бұл Ньютонның екінші немесе артқа интерполяциялық формуласы. Белгісіз функция y – ті жуықтау үшін y = P_n(x) дейміз.

Гаусстың интерполяциялық формуласы.

Айталық бір – бірінен бірдей қашықтықта жатқан 2n+1 интерполяция түйіндері (нүктелері) берілсін: x_-n, x_-(n-1), …, x_-1, x₀, x₁, …, x_n-1, x_n, мұндағы ∆x_i = x_i+1 – x_i = h = const (i = -n, -(n-1), …, n-1, n). Осы түйіндерді y = f(x) функциясының мәндері белгілі дейік y_i = f(x_i) (i=0,. Дәрежесі 2n – нен аспайтын және шарты орындалатын полиномын құру керек.

Полином коэффициенттерін табу идеясы Ньютон полиномы коэффициенттерін табу идеясымен бірдей, яғни сол әдісті қолдана

отырып, табатынымыз: a₀ = y₀, a₁ = , a₂ = , … , a_2n = . Енді q =десек, Гаусстың бірінші интерполяциялық формуласын аламыз:

P(x) = y₀ + q₀ + ²y_-1 + … + ²ⁿy_-n

Бұл формулада келесі орталық айырымдары бар:

y₀, ²y_-1, ³y_-1, ⁴y_-1 т.с.с.

Гаусстың екінші интерполяциялық формуласында келесі орталық айырымдары бар: y_-1, ²y_-1, ³y_-1 т.с.с.

P(x) = y₀ + qy_-1 + ²y_-1 + … + ²ⁿy_-n

Стирлинг және Бессель интерполяциялық формулалары.

Гаусстың бірінші және екінші формулаларының арифметикалық ортасын алсақ Стирлинг формуласы шығады. Ал Бессель формуласы да соған ұқсас болып келеді. Төмендегі формула Стирлинг формуласы деп аталады.

P(x) = y₀ + q+*+* ∆⁴y_-2 + *+* ∆⁶y_-3 + … + + *+ +*∆²ⁿy_-n .

Енді Бессель формуласын келтірейік

P(x) = + (q -)∆y₀ + *+* ∆³y_-2 + *+* ∆⁵y_-2 + + *+ … + +*+ +* ∆²ⁿ⁺¹y_-n .

Лагранж интерполяциялық формуласы.

Жоғарыда айтылған Ньютон, Гаусс, Бессель және Стирлинг интерполяциялық формулалары тек бір – бірінен бірдей қашықтықта жатқан түйіндер үшін ғана жарамды. Ал түйіндердің бір – бірінен ара iқашықтығы әр түрлі болса, онда жалпыланған интерполяциялық формула қажет.Ондай формула – Лагранж интерполяциялық формуласы.

Айталық [a,b] кесіндісінде аргументтің әр түрлі мәндері x₀, x₁, …, x_n берілсін және y = f(x) функциясының сәйкес мәндері де f(x₀) = y₀, f(x₁) = y₁, … , f(x_n) = y_n, белгілі болсын. Бізге, дәрежесі n – нен аспайтын және берілген x₀, x₁, …, x_n түйіндерінде f(x) функциясының сәйкес мәндеріне тең болатын, яғни L_n(x_i) = y_i ( i = 0, 1, 2, …, n) шарты орындалатын, L_n(x) полиномын құру керек.

Алдымен келесі есебін: p_i(x_j) = δ_ij = қанағаттандыратын p_i(x) полиномын құрайық, мұндағы δ_ij – Кронекер өрнегі.

Іздеп отырған полиномымыз x₀, x₁, …, x_i-1, x_i+1, …, x_n n нүктелерінде нөлге айналатындықтан, оны келесі түрде жазуға болады:

p_i(x) = C_i(x – x₀)(x – x₁) … (x – x_i-1)(x_i – x_i+1) … (x – x_n), (7)

Мұндағы C_i – тұрақты коэффициент. Енді (7) формулада x = x_i деп алсақ, және p_i(x_i) = 1 болатынын ескерсек, онда алатынымыз:

C_i(x_i – x₀)(x_i – x₁) … (x_i – x_i-1)(x_i – x_i+1) … (x_i – x_n) = 1

Бұдан C_i = .

Осы мәнді (7) формулаға қойсақ алатынымыз:

P_i(x) = (8)

Енді L_n(x_i) = y_i шартын қанағаттандыратын L_n(x) полиномын табайық. Бұл полином келесі формуламен анықталады

L_n(x) = 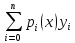. (9)

Расында да, біріншіден, осы құрылған L_n(x) полиномның дәржесі -нен артпайды және екіншіден (6) шарт орындалғандықтан алатынымыз:

L_n(x_j) = ( j = 0, 1, …, n).

Енді (9) формулада p_i(x) – ті орнына қойып, (8) формуладан алатынымыз:

L_n(x) = . (10)

Осы (10) полином формуласы – Лагранж интерполяциялық формуласы.

Енді Лагранж полиномының жалғыздығын дәлелдейік. Ол үшін кері жоримыз. Айталық полиномы L_n(x) полиномынан өзгеше және дәрежесі n – нен үлкен емес бола тұрып, = y_i ( i = 0,1, …, n) шартын қанағаттандырсын. Онда Q_n(x) = - L_n(x) полиномының дәрежесі n – нен артпайды және x₀, x₁, …, x_n n + 1 нүктелерінде нөлге тең болады, яғни Q_n(x) 0, осылай болуы= p_i(x) тепе – теңдігінен шығады, олардың (пен p_i(x) –тің ) бірдей анықталатындығынан шығады. Бұдан = L_n(x). Лагранж полиномының дербес жағдайы: интерполяция түйіндерінің ара қашықтықтары бірдей болса, онда Лагранж интерполяциялық полиномы Ньютон интерполяциялық полиномымен бірдей болады.

Тіпті осы лекцияда көрсетілген барлық интерполяциялық формулаларын, түйіндерді таңдау арқылы, Лагранж интерполяциялық формуласын алуға болады.

(10) Лагранж формуласының ықшам түрін көрсетейік. Ол үшін келесі белгілеулерін енгізейік: . Осы өрнекті дифференциалдап, алатынымыз: Енді десек, онда. Ендеше (10) өрнектен алатынымыз:

Енді x = x_i ( i = 0, 1,…,n) десек, онда

Ендеше (10) – өрнектен алатынымыз: L_n(x) = . (11)

Лагранж формуласының басқа интерполяциялық формулаларынан ерекшелігі: бұл формулаға y_i мәндері айқын кіреді.

Интерполяциялық формулаларының қателіктерінің бағалары.

Лагранж интерполяциялық полиномының қалдық мүшесін R_n(x) = f(x) – L_n(x) деп белгілейік. Енді осы қателікті бағалау үшін f(x) функциясына қосымша талаптар қояйық. х өзгеретін, интерполяция түйіндері жататын, қаралып отырған aаралығында, f(x) функциясының барлық (n + 1) туындылары f’(x), …, f⁽ⁿ⁺¹⁾(x) бар болсын. Енді келесі көмекші функциясын енгізейік

u(x) = f(x) – L_n(x) – k * 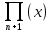(12)

мұндағы к – тұрақты коэффициент, мәні кейін анықталады.

u(x) функциясының x₀, x₁, …, x_n нүктелерінде n+1 түбірі болатыны айқын. Енді, [a,b] кесіндісіндегі, интерполяция түйіндерімен сәйкес келмейтін, әйтеуір бір нүктесінде u(x) функциясының (n+2) - ші түбірі болу шартынан k коэффициентін табамыз. Бұл үшін f() – L_n() – k*= 0 деп ұйғару жеткілікті. Бұдан,

болғандықтан, k = . (13)

k - ның осы мәнінде u(x) функциясының [a,b] кесіндісінде n+2 түбірі болады және [x₀, x₁], [x₁, x₂], …, [x_i, 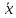], [x_i+1], …, [x_n-1, x_n] кесінділерінің ұштарында нольге айналады.

Ролль теоремасын осы кесінділерінің әрбіреуіне қолданып, u’(x) функциясының [a, b] аралығында кем дегенде n+1 түбірі болатынына көз жеткіземіз. Енді Ролль теоремасын u’(x) туындысына қолданып, u’’(x) екінші туындысының [a, b] аралығында кем дегенде n түбірі болатынына көз жеткіземіз. Осы тұжырымды әрі қарай жалғастыра отырып, u⁽ⁿ⁺¹⁾(x) туындысының, [a, b] аралығында кем дегенде бір түбірі (нөлі) болатынына көз жеткіземіз. Осы түбірді ξ деп белгілейік, яғни u⁽ⁿ⁺¹⁾(ξ) = 0.

(1) формуласынан ,болғандықтан, алатынымыз: u⁽ⁿ⁺¹⁾(x) = f⁽ⁿ⁺¹⁾(x) – k * (n+1)!. Немесе x = ξ болғанда алатынымыз: 0 = f⁽ⁿ⁺¹⁾(ξ) – k * (n+1)!. Бұдан k = (14)

(13) және (14) формулаларының оң жақтарын салыстыра отырып, алатынымыз: , яғни

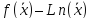= (15)

кез – келген нүкте болғандықтан (15) формуласын келесі түрде жазамыз: R_n(x) = f(x) – L_n(x) = , (16)

Мұндағы ξ х – ке тәуелді және [a, b] кесіндісінде жатыр.

(5) формуласы [a,b] кесіндісінің барлық нүктелерінде, сонымен қатар интерполяция түйіндерінде де дұрыс.

Енді M_n+1 = деп белгілесек, онда біз Лагранж интерполяциялық формуласының абсолютті қателігінің бағасын аламыз:

|R_n(x)| = |f(x) – L_n(x)|* ||, (17)

Мұндағы = (x – x₀)(x – x₁) … (x –x_n).

Ньютонның бірінші интерполяциялық формуласының қалдық мүшесі: R_n(x) = hⁿ⁺¹ * *f⁽ⁿ⁺¹⁾(ξ)

Мұндағы ξ интерполяция түйіндері x₀, x₁, …, x_n – нің біреуі мен алынған интерполяция нүктесі x - тің арасындағы нүкте.

Тура солай, Ньютонның екінші интерполяциялық формуласының қалдық мүшесі: R_n(x) = hⁿ⁺¹ * *f⁽ⁿ⁺¹⁾(ξ)

Мұндағы ξ - интерполяция түйіндері x₀, x₁, …, x_n – нің біреуімен алынған интерполяция нүктесі x - тің арасындағы нүкте.

Кейде f⁽ⁿ⁺¹⁾(ξ) = жуықтау формуласын пайдаланып, Ньютонның 1 –ші интерполяциялық формуласының қалдық мүшесін есептeйміз:

R_n(x) = hⁿ⁺¹ * *Тура солай, Ньютонның 2 –ші интерп.формуласының қалдық мүшесі:

R_n(x) = hⁿ⁺¹ * *

Стирлинг инполяциялық формуласының қалдық мүшесі. Егер айырымдылық кестесінің максималды реті 2n болса және xx₀ - nh, x₀ + nh], онда

R_n(x) = *q(q² – 1²)(q² – 2²)…(q² – n²),

Мұндағы q = ,ξ € x₀ - nh, x₀ + nh]. Немесе

R_n(x) = *q(q² – 1²)(q² – 2²)…(q² – n²)

Бессель инполяциялық формуласының қалдық мүшесі. Егер айырымдылық кестесінің максималды реті 2n+1 болса және xx₀ - nh, x₀ + nh], онда

R_n(x) = *q(q² – 1²)(q² – 2²)…(q² – n²)[q-(n+1)],

Мұндағы q = , ξ € x₀ - nh, x₀ + nh]. немесе

R_n(x) = *q(q² – 1²)(q² – 2²)…(q² – n²)