
- •1. Векторлар жүйесінің рангы. Матрицалардың рангы туралы теоремалар.
- •2. Характеристикалық көпмүше және сызықтық оператордың өзіндік мәндері мен векторлары
- •3. Түйіндес оператор. Сызықтық оператордың және оның түйіндесінің матрицалары арасындағы байланыс
- •4. Унитар кеңістіктегі нормаль оператор
- •5.Унитар кеңістіктердегі өзіне түйіндес және тұрақты таңбалы операторлар.
- •7.Кеңістіктегі түзулердің және жазықтықтардың өзара орналасуы
- •8. Кәдімгі нүктенің ақырсыз аз маңайындағы қисықтың құрылымы
- •9.Бинар қатынастар және оларға қолданылатын амалдар. Бинар қатынастардың қасиеттері. Бинар қатынастың матрицасы
- •10. Пікірлер логикасының формулалары. Формулалардың ақиқаттық мәндері. Формулалардың ақиқаттық кестесі. Пікірлер логикасындағы дедукция туралы теорема.
1. Векторлар жүйесінің рангы. Матрицалардың рангы туралы теоремалар.
---------------------------------------------------------------------------------------
Егер
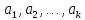 векторлар жүйесінің әрбір векторы
векторлар жүйесінің әрбір векторы
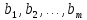 векторлар
жүйесі арқылы, ал
векторлар
жүйесі арқылы, ал
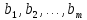 жүйесінің әрбір векторы
жүйесінің әрбір векторы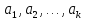 векторлар жүйесі арқылы сызықтық
өрнектелетін болса, онда осы екі жүйеэквивалент
жүйелер деп аталады.
векторлар жүйесі арқылы сызықтық
өрнектелетін болса, онда осы екі жүйеэквивалент
жүйелер деп аталады.
Келесі
екі шартты қанағаттандыратын
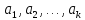 векторлар жүйесінің
векторлар жүйесінің ішкі жүйесінбаза
дейміз:
ішкі жүйесінбаза
дейміз:
(1)
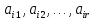 сызықтық тәуелсіз,
сызықтық тәуелсіз,
(2)
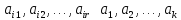 .
.
 векторлар
жүйесінің кез келген базасының қуатын
векторлар
жүйесінің кез келген базасының қуатын
 арқылы белгілейміз де оны
арқылы белгілейміз де оны жүйесініңрангі
деп
атаймыз.
жүйесініңрангі
деп
атаймыз.
Егер
 жүйесінің қандайда бір сызықтық тәуелсіз
жүйесінің қандайда бір сызықтық тәуелсіз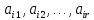 ішкі жүйесінің қуаты жүйенің рангіне
тең болса, онда сол ішкі жүйе база болады.
ішкі жүйесінің қуаты жүйенің рангіне
тең болса, онда сол ішкі жүйе база болады.
Тұжырым. Эквивалент жүйелердің рангілері бірдей болады.
Лемма 1. Сатылы матрицаның жолдар рангі бағандар рангіне тең және ол бастауыш элементтер санына тең болады.
Теорема 1. Кез келген матрицаның жолдар рангі бағандар рангіне тең болады.
Теорема 2. Матрицалардың көбейтіндісінің рангі көбейткіштердің рангілерінен аспайды. Матрицаны керіленетін матрицаға көбейткенде оның рангі өзгермейді.
Дәлелдеу.
 қандайда бір матрицалар болсын
қандайда бір матрицалар болсын
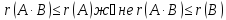
теңсіздіктерін дәлелдеуіміз керек.
 болсын.
Онда
болсын.
Онда
 матрицасының
матрицасының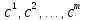 бағандары
бағандары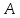 матрицасының бағандары арқылы сызықтық
өрнектеледі.
матрицасының бағандары арқылы сызықтық
өрнектеледі. матрицаларының бағандар жүйелері
өздерінің базалары эквивалент болады.
матрицаларының бағандар жүйелері
өздерінің базалары эквивалент болады.
Осыдан
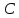 бағандарының кез келген базасы сызықтық
тәуелсіз және
бағандарының кез келген базасы сызықтық
тәуелсіз және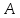 бағандарының базасы арқылы сызықтық
өрнектеледі. Ендеше,
бағандарының базасы арқылы сызықтық
өрнектеледі. Ендеше, бағандарының базасындағы
бағандарының базасындағы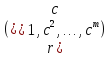 векторлар
векторлар
саны
 бағандарының базасындағы
бағандарының базасындағы векторлар санынан кіші немесе тең
болады. Демек,
векторлар санынан кіші немесе тең
болады. Демек,
Енді
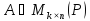 кез келген, ал
кез келген, ал керіленетін матрица болсын. Онда
керіленетін матрица болсын. Онда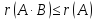 теңсіздігін біз жоғарыда дәлелдедік.
Егер
теңсіздігін біз жоғарыда дәлелдедік.
Егер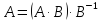 теңдігін пайдалансақ, онда
теңдігін пайдалансақ, онда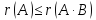 теңсіздігін шығарамыз. Демек,
теңсіздігін шығарамыз. Демек,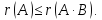
Егер
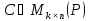 керіленетін матрица болса, онда
керіленетін матрица болса, онда
 және
және
 Демек
Демек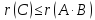 .
.
Теорема дәлелденді.
2. Характеристикалық көпмүше және сызықтық оператордың өзіндік мәндері мен векторлары
Анықтама.
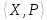 сызықтық кеңістік, ал
сызықтық кеңістік, ал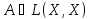 қандайда бір сызықтық түрлендіру болсын.
Онда
қандайда бір сызықтық түрлендіру болсын.
Онда
1)
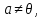

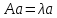 болатын
болатын
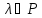 табылады,
табылады,
шарттарын
қанағаттандыратын
 векторы
векторы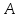 операторыныңөзіндік
векторы
деп,
ал
операторыныңөзіндік
векторы
деп,
ал
 коэффициенті
коэффициенті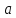 өзіндік векторына сәйкес келетін
өзіндік векторына сәйкес келетін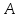 операторыныңөзіндік
мәні
деп
аталады.
операторыныңөзіндік
мәні
деп
аталады.
Матрицаның характеристикалық көпмүшесі деп, өзіндік мәндерін анықтайтын көпмүшені айтамыз.
3. Түйіндес оператор. Сызықтық оператордың және оның түйіндесінің матрицалары арасындағы байланыс
Теорема
1.
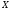 және
және екеуі
де унитар немесе екеуі де Евклид кеңістік
болсын. Онда кез келген
екеуі
де унитар немесе екеуі де Евклид кеңістік
болсын. Онда кез келген сызықтық операторы үшін барлық
сызықтық операторы үшін барлық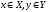 векторларына
векторларына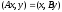 теңдігі орындалатын жалғыз
теңдігі орындалатын жалғыз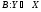 сызықтық операторы табылады.
сызықтық операторы табылады.
Дәлелдеу.
Ақырлы
өлшемді сызықтық кеңістікті бейнелейтін
сызықтық оператор базистік векторлардың
бейнелерімен толық анықталады. Сондықтан,
 және
және кеңістіктерінің қандай да бір
кеңістіктерінің қандай да бір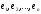 және
және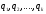 ортонормаланған базистерін белгілеп,
ортонормаланған базистерін белгілеп,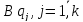 ,
бейнелерін анықтайық.
,
бейнелерін анықтайық. векторы өзінің
векторы өзінің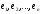 базисіндегі
базисіндегі координаталарымен бірден-бір анықталады.
координаталарымен бірден-бір анықталады.
Бұл
жерде
 немесе оған пара-пар болатын
немесе оған пара-пар болатын шартының дербес жағдайларындағы
шартының дербес жағдайларындағы
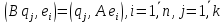 (1)
(1)
теңдіктерін
пайдаланып,
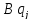 бейнесін
бейнесін

деп анықтаймыз.
Теореманың
дәлелдеуін аяқтау үшін
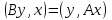 теңдігінің жалпы жағдайда да орындалуын
көрсетуіміз керек.
теңдігінің жалпы жағдайда да орындалуын
көрсетуіміз керек.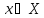 және
және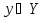 кез келген векторлар, ал
кез келген векторлар, ал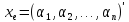 және
және олардың координаталық бағандары болсын.
Онда
олардың координаталық бағандары болсын.
Онда
 .
.
Теорема дәлелденді.
Ескерту 1. Теорема 1 – дің дәлелдеуінде біз операторлардың теңдігін көрсетуіне қолданылатын келесі жалпы тәсілді пайдаландық:
егер
 операторлары үшін
операторлары үшін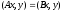 теңдігі барлық
теңдігі барлық және
және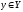 векторлары
үшін орындалса, онда
векторлары
үшін орындалса, онда
 және
және операторлары тең болады.
операторлары тең болады.
Анықтама.
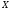 және
және екеуі де бірдей унитар немесе Евклид
кеңістігі, ал
екеуі де бірдей унитар немесе Евклид
кеңістігі, ал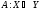 қандай да бір сызықтық оператор болсын.
Кез келген
қандай да бір сызықтық оператор болсын.
Кез келген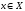 ,
,
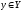 векторларына
векторларына
 теңдігі орындалатын
теңдігі орындалатын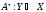 операторы
операторы - ныңтүйіндес
операторы
деп аталады.
- ныңтүйіндес
операторы
деп аталады.
Ескерту 2. Түйіндес оператордың анықтамасынан:
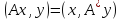 және
және
 екі формула шығады. Оларды: осы
формулаларындағы операторды скаляр
көбейтіндісінің бір аргументінен
екіншісіне көшіріп апарса, ол не
жұлдызшасын жоғалтады, не бір жұлдызша
қосылады дегендей ереже ретінде қолдануға
болады.
екі формула шығады. Оларды: осы
формулаларындағы операторды скаляр
көбейтіндісінің бір аргументінен
екіншісіне көшіріп апарса, ол не
жұлдызшасын жоғалтады, не бір жұлдызша
қосылады дегендей ереже ретінде қолдануға
болады.
Мысал
1.
 .
Шынында да, кез келген
.
Шынында да, кез келген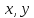 үшін
үшін
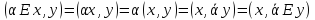 .
Ендеше,
.
Ендеше,
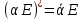 .
Бұл теңдіктің
.
Бұл теңдіктің және
және болғандағы дербес жағдайлары
болғандағы дербес жағдайлары болады.
болады.
Мысал
2.
Егер
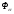 жазықтықты
жазықтықты бұрышына бұру операторы болса, онда
бұрышына бұру операторы болса, онда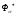 түйіндес операторы сол жазықтықтың
түйіндес операторы сол жазықтықтың бұрышына бұру операторы болады, яғни
бұрышына бұру операторы болады, яғни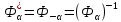 .
Шынында да,
.
Шынында да,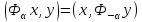 теңдігі жазықтықтағы кез келген екі
теңдігі жазықтықтағы кез келген екі бағытталған кесінді үшін орындалады.
бағытталған кесінді үшін орындалады.
Мысал
3.
Егер
 операторы кез келген
операторы кез келген және бір
және бір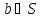 векторлары үшін
векторлары үшін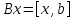 ережесімен анықталған болса, онда
ережесімен анықталған болса, онда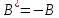 .
Кез келген
.
Кез келген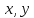 бағытталған кесінділер үшін
бағытталған кесінділер үшін
 Демек,
Демек,
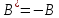 .
.
Оператор мен оның түйіндес оператордың өзара қарапайым байланыстары
 мен
мен
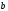 векторлары
векторлары мен
мен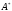 операторларының
операторларының өзіндік мәндеріне сәйкес келетін
өзіндік векторлар болса, онда
өзіндік мәндеріне сәйкес келетін
өзіндік векторлар болса, онда .
.
Шынында
да,
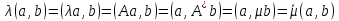 .
Онда
.
Онда
 .
Осыдан
.
Осыдан
 .
.
 ішкі
кеңістігі
ішкі
кеңістігі
 операторының инвариант ішкі кеңістігі
болса, онда оның
операторының инвариант ішкі кеңістігі
болса, онда оның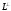 ортогонал толықтауышы
ортогонал толықтауышы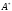 операторының инвариант ішкі кеңістігі
болады.
операторының инвариант ішкі кеңістігі
болады.
 кез
келген вектор болсын.
кез
келген вектор болсын.
 болуы
болуы векторының
векторының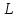 ішкеңістігінің кез келген
ішкеңістігінің кез келген векторына ортогональ болуына пара-пар.
Ендеше,
векторына ортогональ болуына пара-пар.
Ендеше,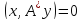 теңдігін көрсетуіміз керек. Түйіндес
оператордың анықтамасы бойынша,
теңдігін көрсетуіміз керек. Түйіндес
оператордың анықтамасы бойынша, ,
ал
,
ал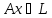 .
Демек,
.
Демек,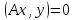 .
.
Бұл байланыстар анықтамадан тікелей шығады.
Түйіндестіктің қасиеттері.
Теорема 1 бойынша, әр сызықтық операторға оның түйіндес операторын сәйкес қоятын ереже бейнелеу болады. Сол түйіндестік бейнелеуінің қасиеттерін қарастырайық. Тек алдын-ала операторлардың теңдігін көрсетуіне қолданылатын келесі жалпы тәсілді берейік:
Теорема
2.
Кез келген
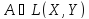 және
және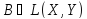 операторлары үшін
операторлары үшін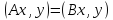 теңдігі барлық
теңдігі барлық және
және векторлары үшін орындалған жағдайда
және тек сол жағдайда ғана
векторлары үшін орындалған жағдайда
және тек сол жағдайда ғана және
және операторлары тең болады.
операторлары тең болады.
Дәлелдеу. Теореманың жеткіліктік тұжырымы айқын, оның қажеттілігін көрсетейік.
Шынында
да,
 теңдігін
теңдігін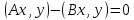 түрінде жазып алып, өрнектейік:
түрінде жазып алып, өрнектейік:
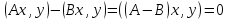 .
Енді
.
Енді
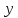 векторы ретінде
векторы ретінде векторын алсақ, одан кез келген
векторын алсақ, одан кез келген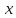 векторына
векторына
орындалатын
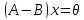 теңдігіне келеміз. Демек, кез келген
теңдігіне келеміз. Демек, кез келген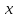 векторы үшін
векторы үшін ,
яғни
,
яғни
 .
Теорема
дәлелденді.
.
Теорема
дәлелденді.
Кез
келген
 сызықтық операторлары және қандай да
бір
сызықтық операторлары және қандай да
бір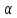 комплекс саны үшін келесі теңдіктер
мен тұжырымдар орындалады:
комплекс саны үшін келесі теңдіктер
мен тұжырымдар орындалады:
(1)
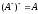 ,
,
(2)
 ,
,
(3)
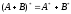 ,
,
(4)
 ,
,
(5)
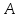 операторы
ерекше емес болса, онда
операторы
ерекше емес болса, онда
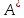 операторы да ерекше емес болады және
операторы да ерекше емес болады және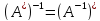 .
.
Дәлелдеу.
Жоғарыдағы тәсіл бойынша,
 теңдігінің орнына қандай да бір
теңдігінің орнына қандай да бір векторларын алып,
векторларын алып,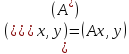 теңдігін дәлелдеуіміз керек. Онда
ескерту 2 –дегі ереже бойынша,
теңдігін дәлелдеуіміз керек. Онда
ескерту 2 –дегі ереже бойынша, .
Бұдан
бұлай
.
Бұдан
бұлай
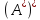 операторын
операторын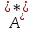 арқылы
белгілейміз де, операторды
өзінің орынынан қозғамай оның екі
жұлдызшасын түсіріп тастауға, не оған
екі жұлдызша тағуға болады
дегендей ережені қолданамыз.
арқылы
белгілейміз де, операторды
өзінің орынынан қозғамай оның екі
жұлдызшасын түсіріп тастауға, не оған
екі жұлдызша тағуға болады
дегендей ережені қолданамыз.Кез келген
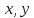 үшін
үшін болғандықтан
болғандықтан болады.
болады.Кез келген
 үшін
үшін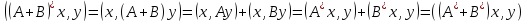 ,
ендеше,
,
ендеше,
 .
.Дәлеледеуі жоқ. Ренжімендер!
Алдымен,
 сызықтық
операторы ерекше емес болсын деп,
сызықтық
операторы ерекше емес болсын деп,
 операторы
да ерекше емес болатынын дәлелдейік.
Кез келген
операторы
да ерекше емес болатынын дәлелдейік.
Кез келген
 және
және
 векторлары үшін
векторлары үшін .
.
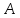 операторы
ерекше емес болғандықтан оның бейнесі
операторы
ерекше емес болғандықтан оның бейнесі
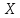 кеңістігіне тең. Демек, кемінде бір
кеңістігіне тең. Демек, кемінде бір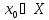 үшін
үшін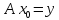 болады.
болады.
Осыдан
 ,
ендеше,
,
ендеше,
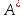 операторы ерекше емес болады.
операторы ерекше емес болады.
Енді
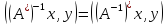 теңдігінің барлық
теңдігінің барлық үшін орындалатынын дәлелдейік.
үшін орындалатынын дәлелдейік. және
және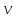 арқылы
арқылы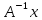 және
және векторларын белгілейік. Онда
векторларын белгілейік. Онда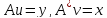 .
Осыдан
.
Осыдан
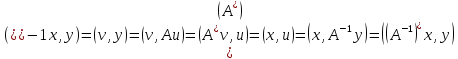 , яғни
, яғни
 .
.
Түйіндес оператордың матрицасы
Анықтама
3.
 қандай
да бір комплекс матрица болсын.
қандай
да бір комплекс матрица болсын.
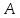 матрицасын аударып алып, оның әрбір
элементін оған түйіндес болатынын
санына ауыстырсақ, онда
матрицасын аударып алып, оның әрбір
элементін оған түйіндес болатынын
санына ауыстырсақ, онда арқылы белгіленетін матрицаны аламыз.
Әлбетте,
арқылы белгіленетін матрицаны аламыз.
Әлбетте,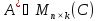 және
және .
. матрицасы
матрицасы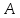 матрицасының түйіндес матрицасы
деп аталады.
матрицасының түйіндес матрицасы
деп аталады.
 нақты
матрицасының түйіндесін табу үшін оны
аудара салу керек, яғни
нақты
матрицасының түйіндесін табу үшін оны
аудара салу керек, яғни
 .
.
Операторлардың түйіндестік амалына сәйкес болатын матрицалардың түйіндестік амалының:
(1)
 ,
,
(2)
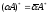 ,
,
(3)
 ,
,
(4)
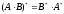 ,
,
(5) егер
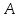 матрицасы
ерекше емес болса, онда
матрицасы
ерекше емес болса, онда
 матрицасы да ерекше емес болады және
матрицасы да ерекше емес болады және .
.
Сызықтық оператордың және оның түйіндесінің матрицалары арасындағы байланыс
Теорема 3. Ортонормаланған базистерде сызықтық оператор мен оның түйіндес операторының матрицалары өзара түйіндес болады.
Дәлелдеу.
 және
және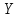 екеуі де унитар (екеуі де Евклид)
кеңістіктері, ал
екеуі де унитар (екеуі де Евклид)
кеңістіктері, ал және
және олардың ортонормаланған базистері
болсын.
олардың ортонормаланған базистері
болсын.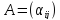 және
және арқылы осы екі оператордың
арқылы осы екі оператордың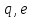 және,сәйкесінше,
және,сәйкесінше,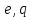 базистер жұптарындағы матрицаларын
белгілейік.
базистер жұптарындағы матрицаларын
белгілейік. теңдігін дәлелдеуіміз керек.
теңдігін дәлелдеуіміз керек.
 элементі
элементі
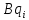 векторының
векторының ортонормаланған базисіндегі
ортонормаланған базисіндегі – координатасы болғандықтан
– координатасы болғандықтан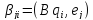
формуласы
бойынша есептеледі, ал
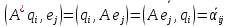 .
Онда барлық
.
Онда барлық үшін
үшін
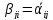 болады.
Демек,
болады.
Демек,
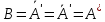 .
.
Салдар
1.
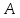 және
және операторларының рангілері өзара тең.
операторларының рангілері өзара тең.
Бұл салдар оператордың рангі оның матрицасының рангіне тең болатынын ескерсе, теоремадан бірден шығады.
Салдар
1.
Кез келген
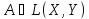 операторы үшін
операторы үшін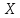 және
және кеңістіктерін:
кеңістіктерін:

ортонональ қосындылар ретінде жіктеуге болады.
Дәлелдеу.
 өзегі және
өзегі және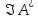 бейнесі өзара ортогональ болатынын
көрсетейік. Ол үшін қандай да бір
бейнесі өзара ортогональ болатынын
көрсетейік. Ол үшін қандай да бір
 алып
және
алып
және
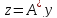 кем дегенде бір
кем дегенде бір үшін болатынын ескере отырып,
үшін болатынын ескере отырып,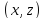 скаляр көбейтіндісін есептейміз:
скаляр көбейтіндісін есептейміз: .
.
Әрине,
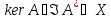 .
Онда
.
Онда теңдігін дәлелдеу үшін оның екі жағындағы
кеңістіктердің өлшемдіктері тең
болатындығын көрсету жеткілікті.
Сонымен,
теңдігін дәлелдеу үшін оның екі жағындағы
кеңістіктердің өлшемдіктері тең
болатындығын көрсету жеткілікті.
Сонымен,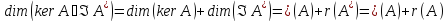 .
.
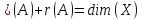 .Демек,
.Демек,
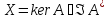 .
Енді бұл теңдікте
.
Енді бұл теңдікте
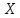 кеңістігін
кеңістігін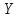 кеңістігіне, ал
кеңістігіне, ал операторын
операторын операторына ауыстырып,
операторына ауыстырып,
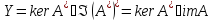 теңдігін
аламыз.
теңдігін
аламыз.
Теорема 4. Унитар (Евклид) кеңістігінің қосалқы базистерінде сызықтық түрлендіру мен оған түйіндес түрлендірудің матрицалары өзара түйіндес болады.
Дәлелдеу.
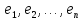 векторлар
жүйесі
векторлар
жүйесі
 унитар немесе Евклид кеңістігінің
қандай да бір базисі, ал
унитар немесе Евклид кеңістігінің
қандай да бір базисі, ал сол кеңістіктің ортоноралаған базисі
болсын.
сол кеңістіктің ортоноралаған базисі
болсын. және
және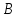 арқылы сол базистердегі
арқылы сол базистердегі сызықтық түрлендіруінің матрицаларын
белгілейік. Онда
сызықтық түрлендіруінің матрицаларын
белгілейік. Онда базисінен
базисінен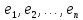 базисіне
базисіне көшу матрицасы үшін
көшу матрицасы үшін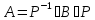 теңдігі орындалады.
теңдігі орындалады. матрицасының бағандары
матрицасының бағандары векторларының ортонормаланған
векторларының ортонормаланған базисіндегі координаталық бағандары
болатынын еске салайық.
базисіндегі координаталық бағандары
болатынын еске салайық.
Теорема
3 бойынша,
 матрицасы
матрицасы
 операторыныың
операторыныың базисіндегі матрицасы болады.
базисіндегі матрицасы болады.
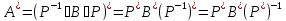 болғандықтан
болғандықтан
 матрицасы
матрицасы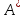 операторының бір
операторының бір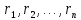 базисіндегі матрицасы болады. Сол
базисіндегі матрицасы болады. Сол базисінің ортонормаланған
базисінің ортонормаланған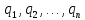 базисіндегі координаталық бағандары
базисіндегі координаталық бағандары матрицасының бағандары болады.
матрицасының бағандары болады.
Енді
тек
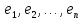 және
және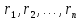 базистерінің қосалқы болатынын көрсету
керек. Ол үшін
базистерінің қосалқы болатынын көрсету
керек. Ол үшін болғанда
болғанда ,
ал
,
ал
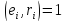 теңдіктерінің
орындалуын көрсетуіміз керек. Бұл
теңдіктердің бәрі бір
теңдіктерінің
орындалуын көрсетуіміз керек. Бұл
теңдіктердің бәрі бір
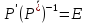 матрицалық теңдігіне пара-пар. Оның
себебі
матрицалық теңдігіне пара-пар. Оның
себебі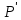 матрицасының жолдары
матрицасының жолдары векторларының, ал
векторларының, ал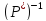 матрицасының бағандары
матрицасының бағандары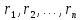 векторларының ортонормаланған
векторларының ортонормаланған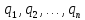 базисіндегі координаталары болуынан.
базисіндегі координаталары болуынан.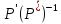 көбейтіндісін есептеп:
көбейтіндісін есептеп:
 керекті
теңдікті аламыз. Теорема дәлелденді.
керекті
теңдікті аламыз. Теорема дәлелденді.
Салдар
2.
 операторы қарапайым құрылысты болған
жағдайда және тек сол жағдайда ғана
операторы қарапайым құрылысты болған
жағдайда және тек сол жағдайда ғана операторы қарапайым құрылысты болады.
Сонымен бірге, егер
операторы қарапайым құрылысты болады.
Сонымен бірге, егер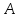 операторы қарапайым құрылысты болса,
онда оның және
операторы қарапайым құрылысты болса,
онда оның және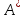 операторының өзіндік векторларынан
тұратын базистерін қосалқы болатындай
құрастыра аламыз.
операторының өзіндік векторларынан
тұратын базистерін қосалқы болатындай
құрастыра аламыз.
Салдар
3.
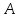 сызықтық түрлендіруінің (жоғарғы) Жордан
түріндегі матрицасы
сызықтық түрлендіруінің (жоғарғы) Жордан
түріндегі матрицасы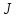 болса,
болса, түрлендіруінің (төменгі) Жордан түріндегі
матрицасы
түрлендіруінің (төменгі) Жордан түріндегі
матрицасы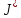 болады. Сонымен,
болады. Сонымен, және
және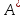 операторларының өзіндік мәндері өзара
түйіндес, ал канондық базистері бір-біріне
қосалқы болады.
операторларының өзіндік мәндері өзара
түйіндес, ал канондық базистері бір-біріне
қосалқы болады.
