- •1. Векторлар жүйесінің рангы. Матрицалардың рангы туралы теоремалар.
- •2. Характеристикалық көпмүше және сызықтық оператордың өзіндік мәндері мен векторлары
- •3. Түйіндес оператор. Сызықтық оператордың және оның түйіндесінің матрицалары арасындағы байланыс
- •4. Унитар кеңістіктегі нормаль оператор
- •5.Унитар кеңістіктердегі өзіне түйіндес және тұрақты таңбалы операторлар.
- •7.Кеңістіктегі түзулердің және жазықтықтардың өзара орналасуы
- •8. Кәдімгі нүктенің ақырсыз аз маңайындағы қисықтың құрылымы
- •9.Бинар қатынастар және оларға қолданылатын амалдар. Бинар қатынастардың қасиеттері. Бинар қатынастың матрицасы
- •10. Пікірлер логикасының формулалары. Формулалардың ақиқаттық мәндері. Формулалардың ақиқаттық кестесі. Пікірлер логикасындағы дедукция туралы теорема.
7.Кеңістіктегі түзулердің және жазықтықтардың өзара орналасуы
Екі жазықтықтың өзара орналасуы.
Π1: А1х+В1у+C1z+D1=0. N1={A1,B1,C1}
Π2: A2x+B2y+C2z+D2=0. N2={A2,B2,C2}
Π1
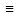 Π2
,
Π2
,
 =
=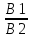 =
=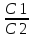 =
=
Π1
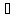 Π2,
Π2,
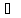
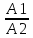 =
= =
=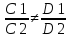
Π1
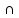 Π2,
Π2,
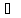
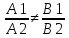 ,
,
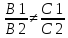 ,
,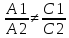
Екі түзудің өзара орналасуы.
P1:
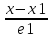 =
=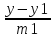 =
=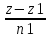 M1=(x1,y1,z1),
a1={e1,m1,n1}
M1=(x1,y1,z1),
a1={e1,m1,n1}
P2:
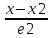 =
= =
=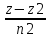 M2=(x2,y2,z2),
a1={e2,m2,n2}
M2=(x2,y2,z2),
a1={e2,m2,n2}
P1
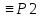
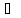 a1
a1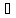 a2
колленеар
және
M1
a2
колленеар
және
M1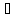 P2
немесе
(M2
P2
немесе
(M2 P1)
P1)
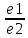 =
=
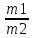 =
=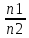
және
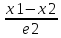 =
=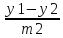 =
=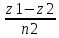 (
(
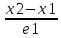 =
=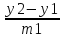 =
=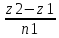 )
)
P1
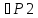
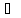 a1
a1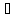 a2
колленеар
және M1
a2
колленеар
және M1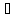 P2
немесе
(M2
P2
немесе
(M2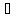 P1)
P1)
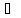
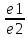 =
=
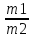 =
=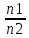
және
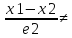
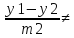
 (
(
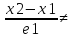
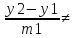
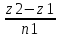 )
)
P1 мен P2 айқас
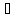 a1
a1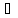 a2
және M1M2,a1,a2
– компланар емес
a2
және M1M2,a1,a2
– компланар емес
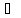
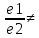
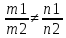 және (M1M2,a1,a2)
және (M1M2,a1,a2)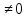
P1
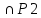
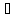 a1
a1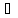 a2
және M1M2,a1,a2
– компланар
a2
және M1M2,a1,a2
– компланар
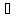

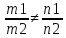 және (M1M2,a1,a2)
және (M1M2,a1,a2)
Түзу мен жазықтықтың өзара орналасуы.
P:
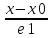 =
=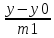 =
=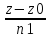 M0=(x0,y0,z0),
a={e0,m0,n0}
M0=(x0,y0,z0),
a={e0,m0,n0}
Π: Ax+By+Cz+D=0 N={A,B,C}
P
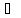 Π
Π
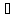 (N,a)=0 және
M0
(N,a)=0 және
M0 Π
Π
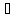
Ae+Bm+Cn=0
Ax0+By0+Cz0+D=0
P
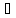 Π
Π
 Ae+Bm+Cn=0
Ae+Bm+Cn=0
Ax0+By0+Cz0+D0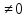
P
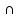 Π
Π
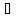 (N,a)
(N,a)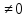
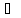 Ae+Bm+Cn
Ae+Bm+Cn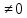
8. Кәдімгі нүктенің ақырсыз аз маңайындағы қисықтың құрылымы
Френе үшжақтығының жазықтықтарына қисықтың проекциялары.
 натурал
параметризацияланған қисықтың теңдеуін
үшінші туындысына дейін Тейлор қатарына
жіктейік
натурал
параметризацияланған қисықтың теңдеуін
үшінші туындысына дейін Тейлор қатарына
жіктейік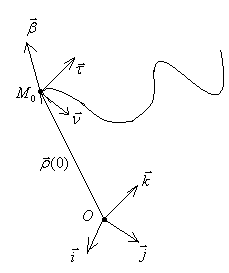
![]()
Векторлық функцияның туындыларының Френе үштігі арқылы жазылуын қолданып
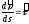

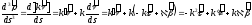
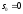 деп
алып,
деп
алып,
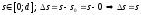
екенін
ескеріп, Тейлор қатарында
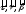 - векторларының бойындағы коэффициенттерін
бөлектеп, жазатын болсақ
- векторларының бойындағы коэффициенттерін
бөлектеп, жазатын болсақ
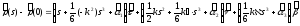
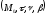 - Френе
реперін
- Френе
реперін
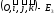 үш
өлшемді кеңістігіміздің базисі ретінде
алайық. Ол үшін
үш
өлшемді кеңістігіміздің базисі ретінде
алайық. Ол үшін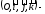 базисін
базисін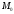 нүктесіне
көшіру және айналдыру жасасаймыз, сонда
нүктесіне
көшіру және айналдыру жасасаймыз, сонда болады. Онда
болады. Онда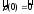 боладыда,
Тейлор қатарымыз келесі түрде жазылады
боладыда,
Тейлор қатарымыз келесі түрде жазылады
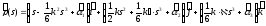
Енді
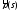 -ті
координаталық түрде жазайық
-ті
координаталық түрде жазайық
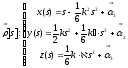 ,бұл
векторлық функцияның годографын
,бұл
векторлық функцияның годографын
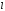 деп
белгілейік
деп
белгілейік
Әр функцияның тек бірінші қосындысын ғана алып қарастырсақ,
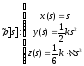 - бұл
- бұл
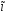 қисығы жеткілікті дәлдікпен берілген
қисығы жеткілікті дәлдікпен берілген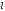 қисықпен беттеседі
қисықпен беттеседі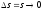 кезде.
кезде.
Осы екі қисықтың жанасушы, нормаль және түзетуші жазықтықтарына проекцияларын қарастырайық.

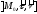 векторларымен
құралатын
векторларымен
құралатын
 жанасушы
жазықтығына проекцияласақ
жанасушы
жазықтығына проекцияласақ
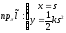 теңдеуі
шығады. Айқындалған функция түрінде
жазатын болсақ
теңдеуі
шығады. Айқындалған функция түрінде
жазатын болсақ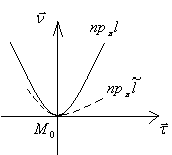
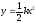
параболасы
шығады. Әрқашанда
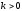 болғандықтан,
параболаның бұтақтары төбеге қарап
тұрады.
болғандықтан,
параболаның бұтақтары төбеге қарап
тұрады.
2)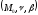 векторларымен
құралатын
векторларымен
құралатын
 нормаль
жазықтығына проекцияласақ
нормаль
жазықтығына проекцияласақ

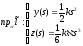 теңдеуі
шығады. Біріншісінен
теңдеуі
шығады. Біріншісінен
 -ті
өрнектеп алып, екіншіге қоямыз
-ті
өрнектеп алып, екіншіге қоямыз
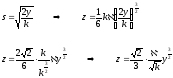
жартылай кубтық парабола деп аталатын қисық шығады.
3)
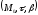 векторларымен
құралатын
векторларымен
құралатын
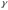 түзетуші
жазықтығына проекцияласақ
түзетуші
жазықтығына проекцияласақ
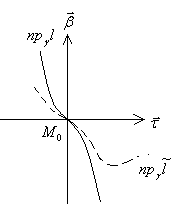
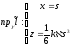 теңдеуі
шығады. Айқындалған функция түрінде
жазатын болсақ z
теңдеуі
шығады. Айқындалған функция түрінде
жазатын болсақ z
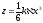
кубтық парабола шығады.
Бұл
зерттеулер қисықтың
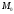 нүктесінің
бір аймағында өзінің Френе
үшжақтығының жазықтықтарына проекциялары
әрқашанда парабола, кубтық парабола
немесе жартылай кубтық парабола болатынын
көрсетеді.
нүктесінің
бір аймағында өзінің Френе
үшжақтығының жазықтықтарына проекциялары
әрқашанда парабола, кубтық парабола
немесе жартылай кубтық парабола болатынын
көрсетеді.
9.Бинар қатынастар және оларға қолданылатын амалдар. Бинар қатынастардың қасиеттері. Бинар қатынастың матрицасы
Анықтама. Бос емес A1, A2,... An жиындары берiлсiн. Онда реттелген элементтер жиыны
A1 A2 ...An {< a1, a2,.. an > : a1 A1 , a2 A2 және an An }
жиыны A1, A2,… An жиындарының декарттық көбейтiндiсi деп аталады.
Олардың элементтерiн n-дiктер (эндiктер, ұзындғы n-ге тең кортеж) деп атаймыз.
Жалпы жағдайда кез келген I индекстік жиыны үшін бұл көбейтiндi

түрiнде жазылады. Мұндағы I жиыны ақырсыз жиын болуы да мүмкiн
Ал nAA...A арқылы А жиынын өзiне өзiн n рет көбейткеннен пайда болған жиын белгіленеді. Ол жиын А жиынының декарттық n-шi дәрежесi деп аталады..
Арнайы бинарлық қатынастар.
Анықтама. Бос емес А жиыны берiлсiн. Мұндағы n – оң бүтiн сан, онда An жиынының кез келген iшкi жиынын А жиынында анықталған n-орынды қатынас деп атаймыз. 1-орынды қатынастар унарлық, 2-орынды қатынастар бинарлық, 3-орынды қатынастар тернарлық қатынастар деп аталады.
R арқылы
А
жиынында
анықталған бинарлық қатынасты белгiлейміз.
Сонымен бірге, (a,b) парының R
қатынасына
тиістілігін (а,b)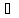 R,
R(a,b)немесе
aRb
таңбалаулардың
бірімен белгілейміз.
R,
R(a,b)немесе
aRb
таңбалаулардың
бірімен белгілейміз.
Қасиеттері:
1.
Егер кез келген x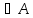 элементi
үшiн (x,x)
элементi
үшiн (x,x)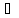 R
болса, онда
R қатынасы
рефлексивтi
қатынас
деп аталады.
R
болса, онда
R қатынасы
рефлексивтi
қатынас
деп аталады.
2.
Егер кез келген x,y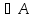 элементтерi
үшiн (x,y)
элементтерi
үшiн (x,y)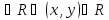 шарты
орындалса, ондаR
қатынасы
симметриялы
деп аталады.
шарты
орындалса, ондаR
қатынасы
симметриялы
деп аталады.
3.
Егер кез келген x,y,z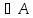 элементтерi үшiн (x,y)
элементтерi үшiн (x,y)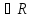 және (y,z)
және (y,z)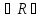
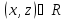 шарты
орындалса, онда қатынасытранзитивтi
деп аталады.
шарты
орындалса, онда қатынасытранзитивтi
деп аталады.
4.
Кез келген x
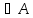 үшiн
(x,x)
үшiн
(x,x) R
болса,
онда қатынасы иррефлексивтi
деп аталады.
R
болса,
онда қатынасы иррефлексивтi
деп аталады.
5.
Кез келген x,y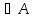 үшiн
(x,y)
үшiн
(x,y)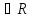 және (y,x)
және (y,x)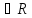 болғандығынанx=y
теңдiгi
орындалса, онда қатынасы антисимметриялы
деп аталады.
болғандығынанx=y
теңдiгi
орындалса, онда қатынасы антисимметриялы
деп аталады.
Анықтамадан рефлексивті және иррефлексивті, симметриялы және антисимметриялы қатынастар біріне бірі толықтауыш жиындар болуы міндетті емес екенін көреміз.
Мысалдар
Ешбір элементі жоқ қатынас, яғни бос қатынас иррефлексивті, симметриялы, антисимметриялы және транзитивті қатынас болады.
Жиын элементтерiнiң теңдiгi және жазықтықтағы немесе кеңiстiктегi түзулердiң параллелдiк қатынастары рефлексивтi, симметриялы және транзитивті қатынастар болады.
Үшбұрыштар арасындағы теңдiк немесе ұқсастық қатынастары рефлексивтi, симметриялы және транзитивтi қатынастар болады.
Жиындар арасындағы ⊆ (iшкi жиын болу) қатынасы мен нақты сандар арасындағы
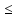 (кiшi немесе тең) қатынастары рефлексивтi,
антисимметриялы және транзитивтi
қатынастарМысалдары.
Ал
(кiшi немесе тең) қатынастары рефлексивтi,
антисимметриялы және транзитивтi
қатынастарМысалдары.
Ал
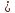 (кiшi ) қатынасы
иррефлексивтi, транзитивтi, бiрақ
симметриялы да, антисимметриялы да
емес қатынас болады.
(кiшi ) қатынасы
иррефлексивтi, транзитивтi, бiрақ
симметриялы да, антисимметриялы да
емес қатынас болады.
Теорема(бөліктеу туралы) .А жиынында анықталған кез келген эквиваленттік қатынас үшін оның эквиваленттілік класстары А жиынының бөліктеуін анықтайды.Керісінше, жиынның әрбір бөліктеуі осы жиындағы өзіне сәйкес эквиваленттілік қатынасты анықтайды.
Дәлелдеуі:
(⇒) ‒A
жиынында анықталған эквиваленттік
қатынас болса, онда оның А жиынының
бөліктеулерін анықтайтын жоғарыда
келтірілген төрт қасиеттен тікелей
шығады.
‒A
жиынында анықталған эквиваленттік
қатынас болса, онда оның А жиынының
бөліктеулерін анықтайтын жоғарыда
келтірілген төрт қасиеттен тікелей
шығады.
(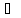 ):
А жиыны мен оның бөліктеуін құратын
ішкі жиындарының тізбегі А1
А2 ,...
Аm,...
):
А жиыны мен оның бөліктеуін құратын
ішкі жиындарының тізбегі А1
А2 ,...
Аm,...
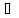 x, y
x, y
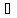 Aүшін x
Aүшін x
 y⇔
i∊I табылып, x,
y
y⇔
i∊I табылып, x,
y
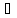 Ai
Ai
шартымен анықтайық. Бұл қатынастың рефлексивті және симметриялы болатыны анықтамадан айқын көрініп тұр. Сондықтан оның транзитивтілігін көрсетсек жеткілікті.
Транзитивтілік.
Қандайда да
бір x, y,
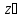 A элементтері
үшін, анықтама бойынша x
A элементтері
үшін, анықтама бойынша x
 y
және y
y
және y z болсын. Онда
i, j ∊
I нөмірлері табылып, x,
y
z болсын. Онда
i, j ∊
I нөмірлері табылып, x,
y
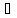 Ai
және y, z
Ai
және y, z
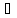 Ai
болады. Яғни, y∊Ai
∩Aj
. Ал (1)
бөліктеу болғандықтан , Ai
=Aj
немесе
i=j. Яғни
x, y,
Ai
болады. Яғни, y∊Ai
∩Aj
. Ал (1)
бөліктеу болғандықтан , Ai
=Aj
немесе
i=j. Яғни
x, y,
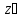 Ai
. Онда x
Ai
. Онда x
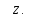 Теорема
дәлелденді.
Теорема
дәлелденді.
a00, a01, a10, a20, a11, a02, a03, a12, a21, a30 (1)
Егер
 ‒
А анықталған эквиваленттілік қатынас
болса, онда А/
‒
А анықталған эквиваленттілік қатынас
болса, онда А/
 =
=
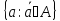 эквиваленттілік кластар жиынын
эквиваленттілік кластар жиынын
 экв.қатынастар
бойынша А жиынында анықталған фактор
– жиын деп
атайды.
экв.қатынастар
бойынша А жиынында анықталған фактор
– жиын деп
атайды.
Бинарлық қатынастарға келесі амалдар қолдануға болады. R – A жиынында анықталған бинарлық қатынас болсын. Онда
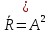
R-1={(a,b): a,b ∊A, (b,a) ∊R}
R1 , R2 – А жиынында анықталған бинарлық қатынастар болса, онда
R1*R2
= {(a,b):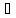 c∊A
⇒(a,c)∊R1
c∊A
⇒(a,c)∊R1
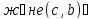 R2}
R2}
Осы амалдардан басқа бинарлық қатынастардың жиын болатынын ескеріп, олардың бірігуін, қиылысуын, айырмаларын , симметриялық айырмаларын және берілген қатынасқа А2 жиынындағы толықтауышын қарастыруға болады.Оларды жиындарға қолданылатын амалдардың
белгілеулеріне сәйкес ∩,⋃, \ және ⊕ таңбаларымен белгілейміз.
Мысалы: ⊕ амалы төмендегідей анықталады.
А⊕В={(a,b): (a,b)}∊A\B немесе (a,b)∊B\A}
Бинарлық қатынастардың матрицасы




 2
3 0 1 0 1
2
3 0 1 0 1
0 0 1 0
 1
4 0 0 0 0
1
4 0 0 0 0
0 0 1 0
ai,j
=