17. Коши интегралдық формуласы

Кез –келген n үшін интегралын есептегенде интегралдау контуры болып тұрған бірлік шеңберді ішінде ішкі нүктесі жататын кез – келген шеңбермен ауыстыруға болады. Бұл жағдайда интегралдың мәні сақталады.

Интегралдау контурларын ауыстырғанда интегралдық мән сақталатын қисықтарды өзара гомотопты қисықтар деп атайды. Ішкі нүктесі координаталар бас нүктесі болып тұрған шеңберлер өзара гомотопты.

Айталық [a,b], [a,b]- бұл γ₀ және γ₁ үзіліссіз қисықтарының параметрлік бейнелеулер болсын. G– ашық жиын және γ₀ ϲ G,

γ₁ ϲ G.

Анықтама. Егер [a,b] x [α,β] C үзіліссіз бейнелеуі бар болса, онда γ₀ қисығы γ₁ қисығына гомотопты деп айтамыз, мұндағы кесіндісі мына шартты қанағаттандырады

t € [a,b], ϕ(t,α) = ϕ₀(t), ϕ(t,β) = ϕ₁(t)

Коши теоремасы. G облысында f(z) голоморфты функциясынан γ₀ және γ₁ үзіліссіз қисықтары бойынша алынған интегралдар нольге тең болады:

=

Бұл теоремаға эквивалентті Коши теоремасының басқаша да түрлерін айтуға болады. арқылы G облысының шекарасын белгілейміз. G – бірбайланысты аймақ болсын.

Коши теоремасы ( бір байланысты аймақ үшін). f(z) бір байланысты аймағында голоморфты функциясы берілсін. Онда бұл функциядан G аймағында жатқан тұйық Г контуры бойынша алынған интеграл нольге тең болады.

Бұл теореманы көп байланысты аймаққа жалпылайық.

Коши теоремасы.( көп байланысты аймақ үшін). f(z) функциясы сырттан Г₀ контурымен, ішінде өзара қиылыспайтын Г₁,Г₂,..., Г_k контурларымен шектелген көп байланысты G аймағында голоморфты функция болсын және f(z) функциясы тұйықталған аймағында үзіліссіз болсын. Онда

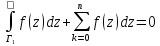
Енді Кошидің интегралдық формуласына тоқталайық. f(z) функциясы Г контурымен шектелген бір байланысты G аймағында аналитикалық функция болсын. G аймағының ішінде жатқан Г контурының ішінен z₀ нүктесін қояйық. Оң бағыт ретінде Г контурының бойымен қозғалғанда G аймағы сол жақта қалатын бағытты аламыз. Онда z₀ € G үшін мына теңдік орындалады:

f(z₀) = dz

Бұл Кошидің интегралдық формуласы. Бұл формула f(z) аналитикалық функциясының контурдағы мәні мен контурдың ішіндегі мәнінің арасындағы байланысты көрсетеді. Кошидің интегралдық формуласын қолданып, тұйық контур ішіндегі аналитикалық функция мәнін функцияның контурдағы мәні бойынша табуға болады.

Сонымен қатар f(z) функциясының G аймағында кез – келген ретті туындысын мына формулалар арқылы табуға болады:

f⁽ⁿ⁾(z₀) = dz

Мұндағы z₀ € G, z , n деп есептейміз.

18. Дәрежелік қатардың жинақтылық радиусы

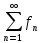қатары, мұндағы

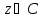дәрежелік қатар деп аталады. Бұл қатардың дербес қосындылары алгебралық көпмүшеліктер,сондықтан

(1)

қатарының қосындысын көпмүшелік ұғымының жалпылануы деуге болады. Дәрежелік қатардың мүшелері C комплекс жазықтығында аналитикалық функциялар. Кез келген дәрежелік қатар үшін бұл қатардөңгелектің ішінде жинақталатын, ал бұл дөңгелектің сыртында жинақталмайтын болатындай R мәні табылады. БұлR саны дәрежелік қатардың жинақталу радиусы деп, ал дөңгелегі жинақталу дөңгелегі деп аталады.шеңберінде, яғни дөңгелектің шекарасында дәрежелік қатар жинақты да, жинақсыз да болуы мүмкін. Қатардың жинақталу радиусы

0. Дәрежелік қатардың жинақталу радиусын табу үшін

R=(2)

Немесе

(3)

формулаларын қолдануға болады. 3-формуланы Коши-Адамар формуласы деп атайды.

Жалпы айтқанда z=нүктесінде бірмәнді және аналитикалық f(z) функциясы бұл нүктенің маңайында келесі Тейлор қатарына жіктеледі:

f(z)=

мұндағы коэффициенттері келесі формуламен анықталады:

(4)

(4) формулалардағы L- центрі нүктесінде болатын шеңбер. Бұл L шеңбері (4) формулада интеграл астындағы функцияның ерекше нүктесі арқылы өтеді. Қатардың жинақтылық радиусы R центрінен оған функцияның ең жақын ерекше нүктесіне дейінгі арақашықтыққа тең болады.