Определение параметров постоянных рент постнумерандо

При разработке условий финансовых контрактов достаточно часто возникают задачи, связанные не с определением наращенной или современной стоимости постоянных рент, а с определением их параметров: срока ренты, годовой процентной ставки и члена ренты.

1. Определение величины члена ренты.

Подобного рода задачи возникают при разработке, например, условий соглашения, предусматривающего равномерное постепенное погашение суммы кредита при заданном его сроке. Здесь возможны два варианта постановки задачи, зависящие от того, какая величина является исходной – наращенная сумма или современная величина. Если сумма долга определена на какой-либо момент в будущем, то логично приравнять ее наращенной сумме, тогда величина члена ренты легко находится на основе формулы (69)

R = S/s_n,i . (84)

Если же размер долга определен на некоторый начальный момент, то эта сумма приравнивается к современной величине ренты и величина члена ренты определится с помощью формулы (74)

R = A/a_n,i. (85)

На основе формул (71) – (78) нетрудно определить R и для других условий ренты.

2. Расчет срока ренты и ставки процента

При разработке условий финансовых соглашений иногда сталкиваются с необходимостью определения срока ренты в зависимости от заданных условий. Расчет срока имеет смысл в том случае, когда заданы A, S, R, i (для годовой ренты m = 1) или аналогичные условия для p-срочных рент. Данная задача решается простым преобразованием формул, определяющих A и S. Так, для годовой ренты с ежегодным начислением процентов находим

^, (86)

^. (87)

При анализе формул (86) и (87) становится очевидным, что они позволяют определить значение n только при определенных условиях. Например, n, определенная по формуле (71) будет положительным числом только в том случае, когда илиR > A·i. Иначе говоря, если A – текущее значение долга, которое приравнено современной стоимости ренты, погашающей этот долг, то за конечное число выплат этот долг будет погашен. Если же R=A·i, то в этом случае n =  и члены ренты будут покрывать только текущие начисленные проценты. Если R < A·i, то начисленные проценты превышают член ренты и погашение долга размером A выплатой ренты с членом R невозможно.

Для определения величины процентной ставки можно воспользоваться специальным пакетом прикладных программ или методом линейной интерполяции, итерационным методом, можно использовать первые три-четыре члена разложения бинома Ньютона и пр.

Пример 49.

Допустим, что 1 января 2002 года на счете в банке у клиента должно быть 1000 руб. По состоянию на 1 января 1999 года на счете клиента есть 400 руб. Какую сумму должен перечислять в банк каждые последующие полгода, если процентная ставка по депозиту равна 8%, а проценты начисляются по полугодиям?

Всего за указанный период клиент будет переводить деньги 6 раз.

Таким образом, по условию задачи S = 1000 руб., i = 0,08, m = p = 2, n=3.

Поскольку на 1 января 1999 года на счете находится 400 руб., на 1 января 2002 года эта сумма обратится в 506,13 руб. [400 ∙ (1 + 0,.08/2)^2∙3].

Следовательно, за 6 периодов клиент должен будет внести сумму S_доп:

S_доп = 1000 – 506,13 = 493,87 руб.

Поскольку получим:

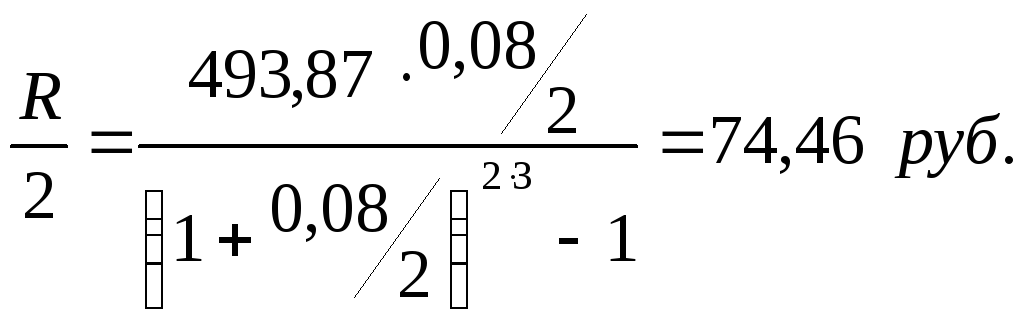
Это означает, что каждые полгода клиент должен вносить на счет в банке 74,46 руб.