
- •В.Н. Краев Практикум по финансовой математике
- •Владимир 2006 в Примечанияведение
- •Инвестиционная деятельность
- •Глава 1 знакомит читателя с сущностью и задачами финансово-экономических расчетов, оценкой финансово-экономических платежей, планированием погашения задолженности.
- •Раздел 1. Простые и сложные проценты
- •В Примечанияремя как фактор в финансовых расчетах. Виды процентных ставок
- •1 Примечания.2. Простые проценты
- •Переменные ставки Примечания
- •Реинвестирование
- •Расчет процентов для краткосрочных ссуд
- •1 Примечания.3 Дисконтирование и учет по простым процентным ставкам основные понятия
- •Первоначальная сумма Наращение Наращенная сумма
- •Процентная ставка (Возвращаемая сумма)
- •Математическое дисконтирование
- •Банковский или коммерческий учет (учет векселей)
- •Дисконтирование с использованием простой учетной ставки
- •Ставка наращения и учетная ставка. Эквивалентные ставки
- •Ставки Прямая задача Обратная задача
- •Эквивалентные ставки
- •Финансовые вычисления на основе сложных процентов
- •В конце n-го года наращенная сумма будет равна
- •Переменные ставки
- •Начисление процентов при дробном числе лет
- •Рост по сложным и простым процентам
- •Срок ссуды и формулы удвоения
- •1.7. Номинальная и эффективная ставки номинальная ставка
- •Эффективная ставка
- •Дисконтирование с использованием сложных процентов
- •Наращение по сложной учетной ставке
- •Мажорантность множителей наращения и дисконтных множителей
- •Эквивалентный переход от одной ставки к другой
- •4.1 Финансовая эквивалентность обязательств
- •Консолидирование задолженности
- •Постоянные финансовые ренты
- •Основные понятия. Классификация рент
- •Определение наращенной суммы постоянных рент постнумерандо
- •Годовая рента
- •2.4. Определение современной стоимости постоянных рент постнумерандо
- •Годовая рента
- •Определение параметров постоянных рент постнумерандо
- •Наращенные суммы и современные стоимости других видов постоянных рент
- •Конверсии рент
- •Изменение параметров рент
Эквивалентный переход от одной ставки к другой
В связи с тем, что контракты могут быть составлены с использованием различных видов ставок, то для сопоставления их доходности возникает необходимость в установлении правил эквивалентного приведения различных ставок к ставке одного вида. Формулы, устанавливающие правила эквивалентного перехода от одной ставки к другой, выводится на основе принципа финансовой эквивалентности результатов наращения (или дисконтирования) по этим ставкам. Следовательно, для их получения достаточно приравнять соответствующие множители наращения (или дисконтирования).
Н айдем,
например, ставку простых процентов,
эквивалентную ставке сложных процентов.
Очевидно, что для этого достаточно
написать равенство
айдем,
например, ставку простых процентов,
эквивалентную ставке сложных процентов.
Очевидно, что для этого достаточно
написать равенство
1 + n ∙ in = (1 + ic)n,
где in – ставка простых процентов; ic – ставка сложных процентов, тогда
![]() (51)
(51)
![]() (52)
(52)
то есть ставки существенно зависят от срока начисления процентов.
Для простой учетной ставки и сложной ставки имеем:
![]()
тогда получим:
![]() (53)
(53)
и
![]() (54)
(54)
Эквивалентность других ставок выводится аналогично.
Пример 33.
Кредит предоставлен из условия 6% годовых по ставке сложных процентов. Каковы будут эквивалентные ставки простых процентов при сроках кредита: а) 10 лет; б) 160 дней, k = 365 дней.
|
Дано: ic = 6% na = 10 лет nб = 160 дней k = 365 дней |
Решение: Используя выражение (52) для случая а) получим:
для случая б):
|
|
in - ? | |
|
|
П ример
34.
ример
34.
Контракт предусматривает начисление сложных процентов при ставке 8% годовых. Срок ссуды 2 года, начисление процентов производится поквартально. Требуется определить простую ставку, эквивалентную этим условиям.
|
Дано: jc = 8% n = 2 года m = 4 |
Решение: Приравнивая множители наращения, получим:
|
|
iп - ? | |
|
|
КОНВЕРСИЯ ПЛАТЕЖЕЙ. ЭКВИВАЛЕНТНОСТЬ ПРОЦЕНТНЫХ СТАВОК
4.1 Финансовая эквивалентность обязательств
В практике нередко возникают случаи, когда необходимо заменить одно обязательство другим, например с более отдаленным сроком платежа, досрочно погасить задолженность, объединить несколько платежей в один (консолидировать платежи) и т.п. В таких ситуациях неизбежно возникает вопрос о принципе, на котором должно базироваться изменение контракта. Таким общепринятым принципом является финансовая эквивалентность платежей, который предполагает неизменность финансовых отношений сторон до и после изменения условий контракта или сделки.
Эквивалентными считаются такие платежи, которые, будучи «приведенными» к одному моменту времени, оказываются равными. Приведение осуществляется путем дисконтирования к более ранней дате или, наоборот, наращением суммы платежа (если эта дата относится к будущему).
По существу, принцип эквивалентности следует из формул наращения и дисконтирования, связывающих величины P и S: сумма P эквивалентна сумме S при принятой процентной ставке и методе ее начисления. Две суммы S1 и S2, выплачиваемые в разные моменты времени, считаются эквивалентными, если их современные (или наращенные) величины, рассчитанные по одной и той же процентной ставке и на один момент времени, одинаковы. На рис. 9 приведены схемы, иллюстрирующие принцип финансовой эквивалентности.
а)

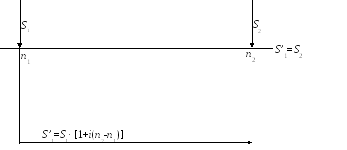
б )
)
Рис. 9. Схемы, иллюстрирующие принцип финансовой эквивалентности
Пример 35.
Долговое обязательство в 1000 руб. со сроком погашения 120 дней заменяется платежом со сроком погашения 180 дней. Простая процентная ставка – 10%. Найти сумму заменяющего платежа. k = 360 дней.
|
Д S1 = 1000 руб. n1 = 120 дней n2 = 180 дней i = 10% |
Решение: Срок погашения долгового обязательства продлевается на 60 дней (180-120), следовательно, сумму заменяющего платежа можно найти нарастив 1000 руб. на 60 дней по ставке 10% |
|
S2 - ? |
Графическая иллюстрация
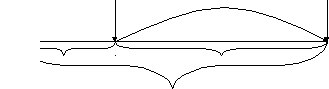 S1
= 1000 руб. наращение S2
- ?
S1
= 1000 руб. наращение S2
- ?
i = 10%
n = 60 дней
120 дней 60 дней
180 дней
Записываем
уравнение эквивалентности:
![]()
В этом примере используется схема а) рис.9. Платежи S2 и S1 – эквивалентны.
Пример 36.
Сформулируем предыдущую задачу по другому. Долговое обязательство в 1000 руб. со сроком погашения 20 мая было погашено 20 июля в сумме 1016,67 руб. Простая процентная ставка – 10%. k = 360 дней. Проценты обыкновенные. Определить эквивалентность платежей.
|
Дано: S1 = 1000 руб. S2 = 1016,67 руб. i = 10% n = 60 дней |
Решение: В |
|
S1 = S2 - ? |
i = 10% n = 60 дней
дисконтирование
Уравнение
эквивалентности:

Платежи – эквивалентны.

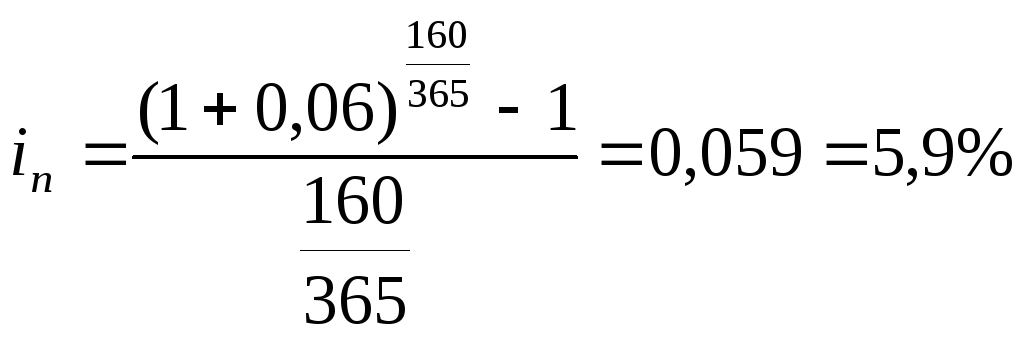
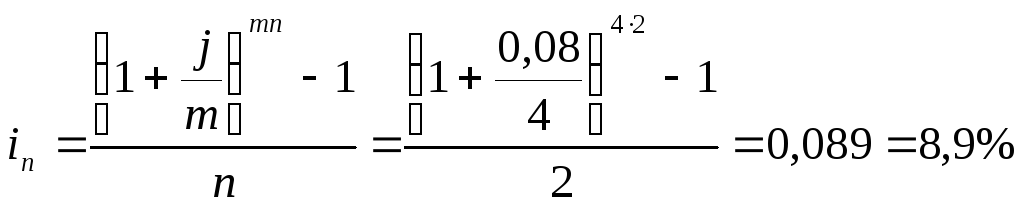
 ано:
ано: оспользуемся
схемой б) рис.9, тогда графически задача
будет выглядеть так
оспользуемся
схемой б) рис.9, тогда графически задача
будет выглядеть так

 S1
- ? S2
=1016,67
S1
- ? S2
=1016,67