9.3. Парабола

З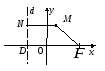ададим на плоскости прямуюи точку

фокус, директриса.

Опр. Параболой называется множество точек

плоскости, для которых расстояние от фокуса

равно расстоянию до директрисы.

Составим уравнение параболы.

параметр параболы, Пустьпринадлежит параболе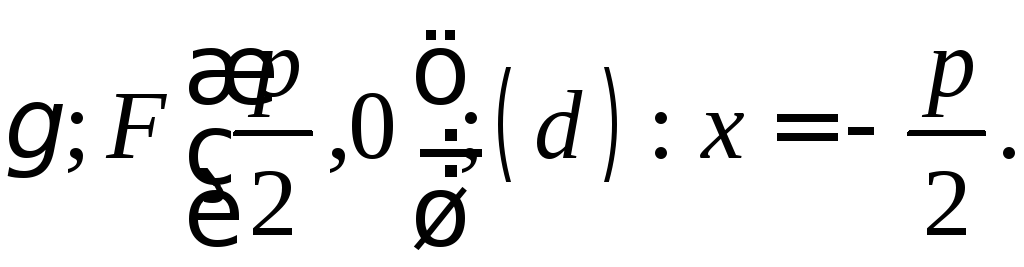

(9)

Упростим уравнение (9):

(10)

Итак, координаты любой точки параболы удовлетворяют уравнению (10). Покажем, что точка, координаты которой удовлетворяют уравнению (10), принадлежит параболе, то есть

(10)(9)Из (10)

Уравнение (10)-каноническое уравнение параболы.

Исследование формы

1.Парабола симметрична относительно

оси

2.Вся кривая расположена справа от

3. Точка вершина параболы.

4. При ордината

5. Чем больше параметр параболы, тем шире расходятся ветви.

6.(по аналогии с эллипсом и гиперболой).

9.4. Кривые 2-го порядка как конические сечения

Еще древнегреческие математики трактовали эллипс, гиперболу и параболу как конические сечения. А именно: сечением любого круглого

конуса плоскостью определяется кривая,

которая может быть лишь эллипсом,

гиперболой или параболой. При этом, если

плоскость пересекает только одну полость

конуса и по замкнутой кривой, то эта кривая

есть эллипс; если секущая плоскость

пересекает только одну полость конуса и по

незамкнутой кривой, то эта кривая –

парабола; если плоскость пересекает обе

полости конуса, то эта кривая – гипербола.

Такая трактовка кривых 2-го порядка является одним из выдающихся успехов античной математики. Едва ли можно переоценить значение конических сечений как для чистой, так и для прикладной математики

(например, орбиты планет и орбиты электронов в атоме водорода являются коническими сечениями). Не удивительно, что классическая, возникшая в Древней Греции теория конических сечений и в наши дни составляет необходимую часть математического образования. Через две тысячи лет были открыты замечательные проективные свойства конических сечений.

§10. Общее уравнение линии 2-го порядка

и приведение его к каноническому виду

В аффинной системе координат общее уравнение линии 2-го порядка имеет вид:

(11)

Коэффициенты не равны ) одновременно.

Приведем уравнение (11) к каноническому виду. Для этого будем рассматривать его в ортонормированном репере

Часть 1. Преобразуем систему координат поворотом на угол вокруг начала.

Запишем формулы преобразования:

(12)

Подставим (12) в (11):

В новых переменных уравнение запишем так:

(11’)

где(13)

1/ Если то подберем уголтак, чтобы уравнение (11’) не содержало члена с произведениемто есть чтобы

Определитель равен ) тогда и только тогда, когда его строки пропорциональны:

(14’)

(14)

Система (14) однородных уравнений имеет нетривиальное решение, если её определитель равен 0:

(15)

Опр. Уравнение (15) называется характеристическим уравнением линии 2-го порядка.

Покажем, что его коэффициенты не зависят от выбора ортонормированного репера.

Из (13):

2.По предположению поэтому дискриминант уравнения (15):

Значит, характеристическое уравнение (15) всегда имеет действительные и различные корни иИз (14) следует:

(16)

По формулам Виета: и

Тогда

Любой из углов можно взять за угол поворота осей, при этом исчезает член с произведением

Найдем коэффициенты уравнения (11’) из системы (13), учитывая(14’).

Итак, для любой линии 2-го порядка, заданной в ортонормированном репере уравнением (11), существует ортонормированный репер в котором её уравнение имеет вид (17):

(17)

Пример. Приведите к каноническому виду уравнение:

∆ 1.Запишем характеристическое уравнение данной кривой и найдем его корни.

(15)

2. В новой системе координат уравнение имеет вид:

(17)- эллипс.

3. Запишем формулы преобразования координат.

(16)или

(12)

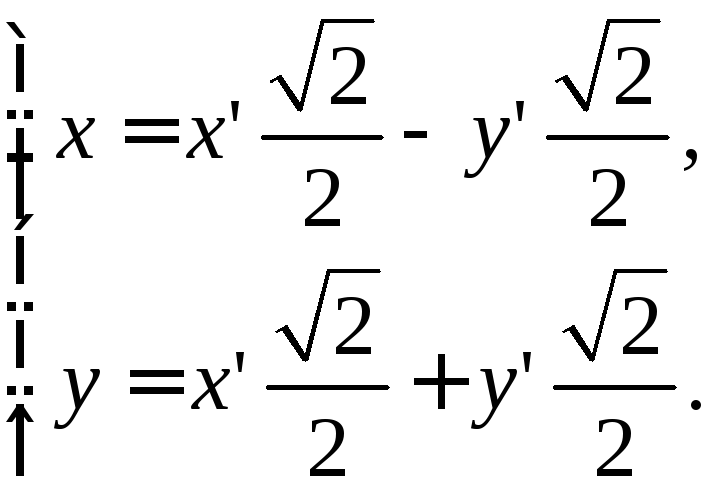
4. Чертеж.