
- •Безверхняя и. С.
- •§2. Линейные операции над векторами
- •§3. Линейная зависимость векторов
- •§4. Координаты вектора
- •§5. Скалярное произведение векторов
- •§6. Направляющие косинусы вектора
- •§7. Векторное произведение векторов.
- •§8. Смешанное произведение векторов.
- •Раздел 2. Метод координат на плоскости
- •§1. Аффинная система координат
- •§ 2. Деление отрезка в данном отношении
- •§3. Декартова прямоугольная система координат
- •§ 4. Ориентация плоскости
- •§5. Полярные координаты
- •§6. Алгебраическая линия
- •§7. Прямая линия на плоскости
- •7.1.Различные уравнения прямой
- •7.3. Взаимное расположение двух прямых
- •7.4. Прямая в декартовой прямоугольной системе координат
- •§8. Формулы преобразования координат
- •§ 9. Линии 2-го порядка
- •9.1. Эллипс
- •9.2. Гипербола
- •9.3. Парабола
- •9.4. Кривые 2-го порядка как конические сечения
- •§10. Общее уравнение линии 2-го порядка
- •Часть 1. Преобразуем систему координат поворотом на угол вокруг начала.
- •Часть 2. Исследуем уравнение (17):
- •Раздел 3. Система координат в пространстве
- •§1. Плоскость
- •§2. Взаимное расположение двух плоскостей
- •§3.Плоскость в дпск. Основные задачи.
- •§4. Прямая в пространстве.
- •§5. Поверхности 2-го порядка
- •5.1. Понятие поверхности 2-го порядка
- •5.2. Цилиндрические поверхности.
- •5.3. Конические поверхности
- •5.4. Эллипсоид
- •5.5 Однополостный гиперболоид
- •5.6. Двуполостный гиперболоид
- •5.7. Эллиптический параболоид
- •5.8. Гиперболический параболоид
- •Вариант индивидуального задания.
- •Литература
§7. Прямая линия на плоскости
7.1.Различные уравнения прямой
Будем рассматривать прямую в некоторой аффинной системе координат.
7 .1.1.Каноническое
уравнение прямой
.1.1.Каноническое
уравнение прямой
Опр. Ненулевой вектор, параллельный прямой,
называется направляющим вектором прямой.
Зададим
прямую на плоскости точкой
![]() и направляющим вектором
и направляющим вектором![]()
Возьмем
на прямой
![]() произвольную точку
произвольную точку![]()
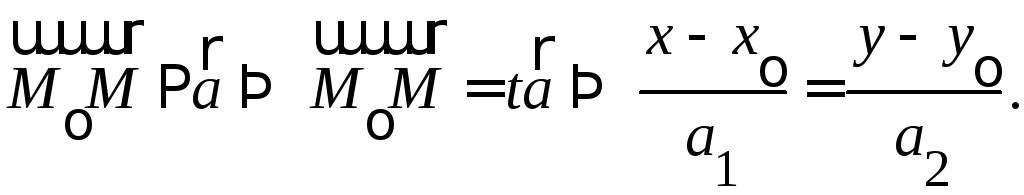 Это каноническое уравнение прямой.
Это каноническое уравнение прямой.
7.1.2.Параметрические уравнения
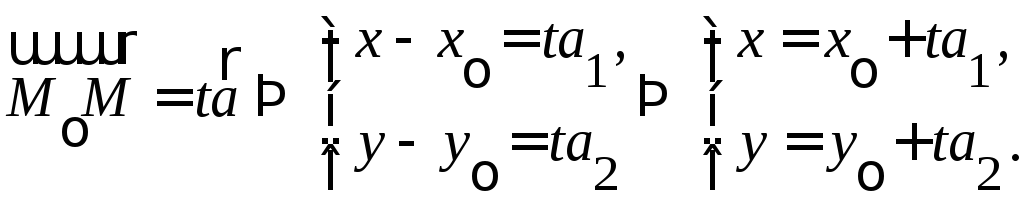 Параметрические
уравнения.
Параметрические
уравнения.
7.1.3. Уравнение прямой через две точки.
![]()
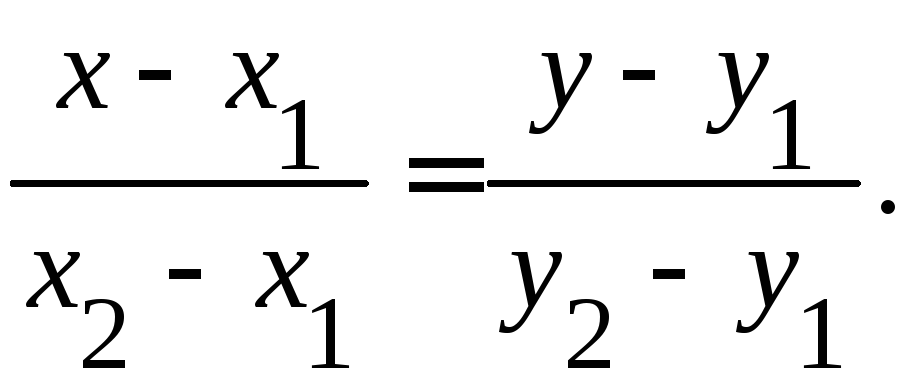
7.1.4. Уравнение прямой в отрезках
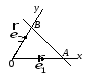 Точки пересечения
прямой с осями координат
Точки пересечения
прямой с осями координат
![]()


Какую прямую нельзя задать уравнением в отрезках?
7.1.5. Уравнение прямой с угловым коэффициентом.
![]()
![]()

Опр.
Назовем отношение
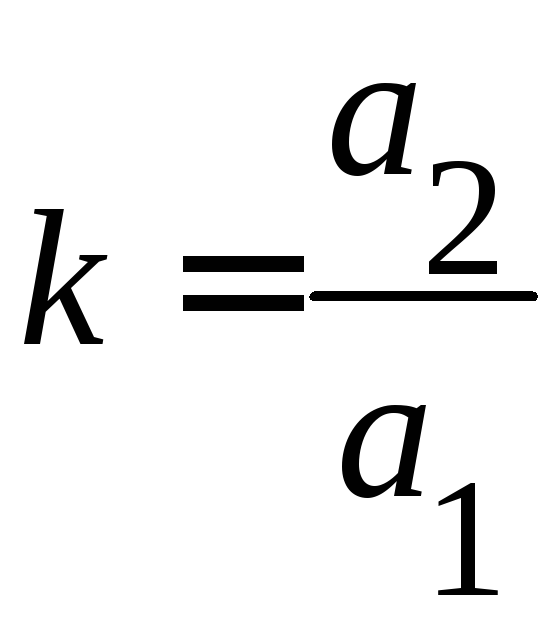 -угловым
коэффициентом прямой
-угловым
коэффициентом прямой
![]()
Можно
доказать, что угловой коэффициент прямой
не зависит от выбора направляющего
вектора прямой и в дпск он равен тангенсу
угла наклона прямой к оси
![]()
7.1.6. Общее уравнение прямой
Преобразуем каноническое уравнение прямой:

Ax+By+C=0. (11)
Итак,
всякая прямая на плоскости определяется
уравнением 1 степени относительно
переменных
![]()
Направляющий
вектор
![]()
Обратно:
всякое уравнение (11), где
![]() определяет на плоскости прямую,
параллельную вектору
определяет на плоскости прямую,
параллельную вектору![]()
Следовательно, справедлива
Теорема
9. Всякое
уравнение 1 степени с двумя переменными
![]() определяет на плоскости прямую и только
прямую.
определяет на плоскости прямую и только
прямую.
Иначе: всякая алгебраическая линия 1 порядка есть прямая линия.
7.1.7. Неполные уравнения прямой. Построение прямой.
Уравнение прямой
![]() все коэффициенты которого отличны от
0, называется полным. Если же какие-то
коэффициенты в нем равны 0, имеем неполное
уравнение. Для построения прямой по
уравнению достаточно знать две её точки
или точку и направляющий вектор
все коэффициенты которого отличны от
0, называется полным. Если же какие-то
коэффициенты в нем равны 0, имеем неполное
уравнение. Для построения прямой по
уравнению достаточно знать две её точки
или точку и направляющий вектор
![]()
Пусть
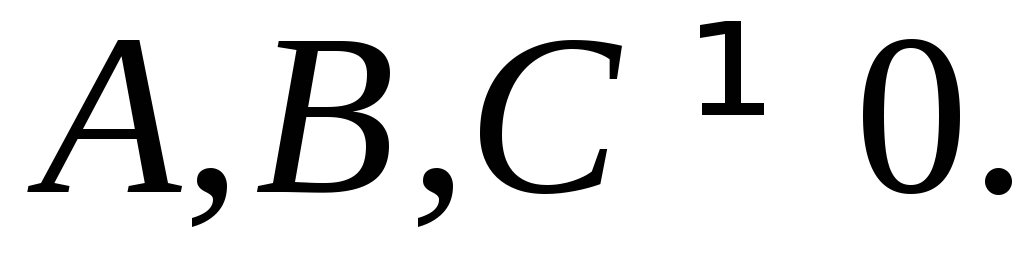 Имеем полное уравнение
Имеем полное уравнение Приведем его к уравнению в отрезках:
Приведем его к уравнению в отрезках: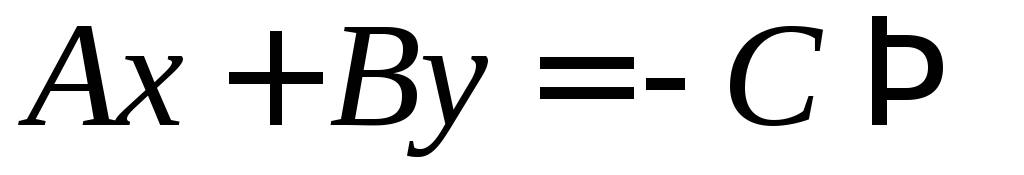
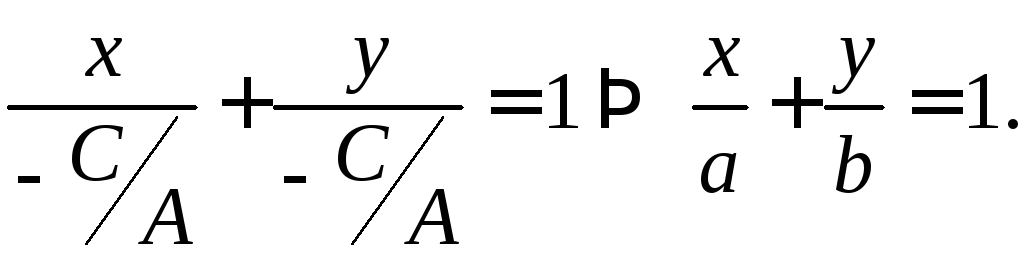
Пример.
![]()
2)
![]() прямая проходит через начало координат.
прямая проходит через начало координат.
Пример.
![]()
3)
![]()
![]()
Пример.
![]()
4)
![]()
![]()
5)
![]()
6)
![]()
Задача.
Найдите направляющие векторы и постройте
в аффинной системе координат прямые:
![]()
![]()
7.2.
Геометрический смысл знака трехчлена
![]()
Прямая
![]() делит плоскость на две полуплоскости.
Координаты точек, принадлежащих прямой,
обращают уравнение в тождество. Можно
доказать, что для координат точек из
одной полуплоскости (той, куда направлен
вектор
делит плоскость на две полуплоскости.
Координаты точек, принадлежащих прямой,
обращают уравнение в тождество. Можно
доказать, что для координат точек из
одной полуплоскости (той, куда направлен
вектор![]() )
выполняется неравенство
)
выполняется неравенство![]() для координат точек другой полуплоскости
для координат точек другой полуплоскости![]() В этом состоит геометрический смысл
знака трехчлена
В этом состоит геометрический смысл
знака трехчлена![]()
Задача.
Пересекает
ли прямая
![]() отрезок с концами
отрезок с концами![]()
7.3. Взаимное расположение двух прямых
7.3.1. Выясним, при каких условиях два уравнения
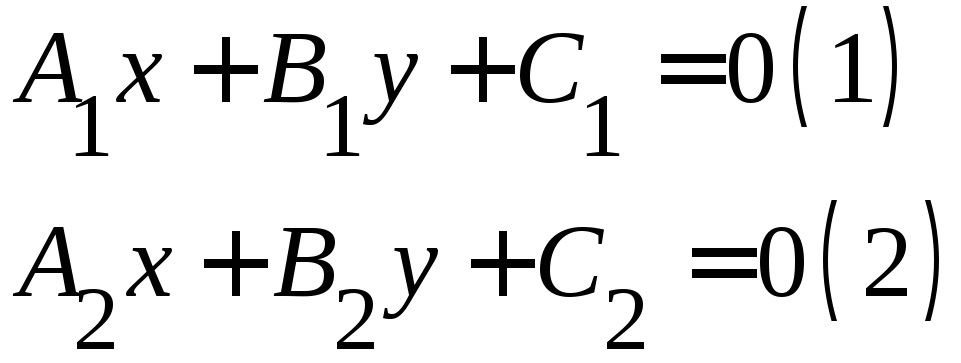
определяют одну и ту же прямую?
Теорема 10. Для того, чтобы уравнения (1) и (2) определяли одну и ту же прямую, необходимо и достаточно, чтобы их коэффициенты были пропорциональны.
∆ Пусть (1) и (2) определяют одну и ту же прямую.
Необходимость
![]() Направляющие векторы этих прямых:
Направляющие векторы этих прямых:
![]() и
и
![]() коллинеарны, следовательно,
коллинеарны, следовательно,
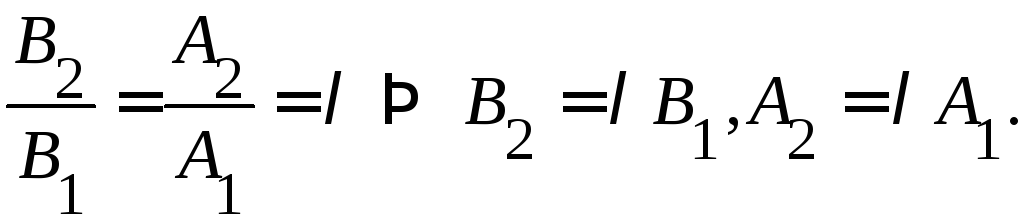
Возьмем
на прямой точку
![]() ,
подставим её координаты в уравнения
(1) и (2) и вычтем, умножив (1) на
,
подставим её координаты в уравнения
(1) и (2) и вычтем, умножив (1) на![]()
![]() √
√
Достаточность![]() Если коэффициенты уравнений (1) и (2)
пропорциональны, то (2) можно записать
так:
Если коэффициенты уравнений (1) и (2)
пропорциональны, то (2) можно записать
так:
![]() Но уравнениям (2)
и (3) удовлетворяют координаты одних и
тех же точек, следовательно, они определяют
одну и ту же прямую.
▲
Но уравнениям (2)
и (3) удовлетворяют координаты одних и
тех же точек, следовательно, они определяют
одну и ту же прямую.
▲
7.3.2. Выясним взаимное расположение двух прямых, заданных в некоторой аффинной системе координат уравнениями (1) и (2).Возможны два случая.
1.![]() В этом случае прямые пересекаются, и
для нахождения их точки пересечения
надо решить систему уравнений (1),(2).
В этом случае прямые пересекаются, и
для нахождения их точки пересечения
надо решить систему уравнений (1),(2).
2.![]() или
или![]()
При
![]()
 При
При![]()
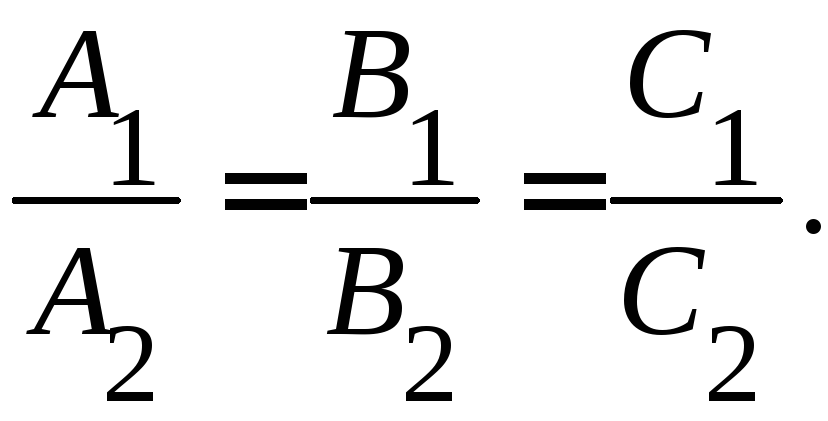
Вывод.
1)
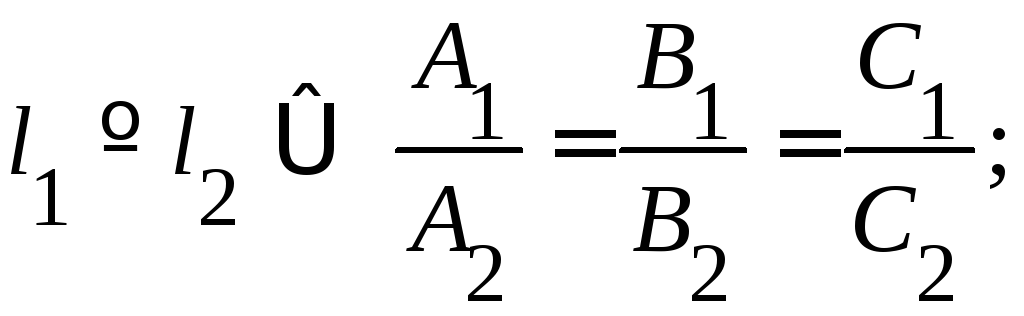
2)

3)

Задача.
Через точку
![]() провести прямую, параллельную прямой
провести прямую, параллельную прямой
![]() Решить двумя
способами.
Решить двумя
способами.
