
- •Безверхняя и. С.
- •§2. Линейные операции над векторами
- •§3. Линейная зависимость векторов
- •§4. Координаты вектора
- •§5. Скалярное произведение векторов
- •§6. Направляющие косинусы вектора
- •§7. Векторное произведение векторов.
- •§8. Смешанное произведение векторов.
- •Раздел 2. Метод координат на плоскости
- •§1. Аффинная система координат
- •§ 2. Деление отрезка в данном отношении
- •§3. Декартова прямоугольная система координат
- •§ 4. Ориентация плоскости
- •§5. Полярные координаты
- •§6. Алгебраическая линия
- •§7. Прямая линия на плоскости
- •7.1.Различные уравнения прямой
- •7.3. Взаимное расположение двух прямых
- •7.4. Прямая в декартовой прямоугольной системе координат
- •§8. Формулы преобразования координат
- •§ 9. Линии 2-го порядка
- •9.1. Эллипс
- •9.2. Гипербола
- •9.3. Парабола
- •9.4. Кривые 2-го порядка как конические сечения
- •§10. Общее уравнение линии 2-го порядка
- •Часть 1. Преобразуем систему координат поворотом на угол вокруг начала.
- •Часть 2. Исследуем уравнение (17):
- •Раздел 3. Система координат в пространстве
- •§1. Плоскость
- •§2. Взаимное расположение двух плоскостей
- •§3.Плоскость в дпск. Основные задачи.
- •§4. Прямая в пространстве.
- •§5. Поверхности 2-го порядка
- •5.1. Понятие поверхности 2-го порядка
- •5.2. Цилиндрические поверхности.
- •5.3. Конические поверхности
- •5.4. Эллипсоид
- •5.5 Однополостный гиперболоид
- •5.6. Двуполостный гиперболоид
- •5.7. Эллиптический параболоид
- •5.8. Гиперболический параболоид
- •Вариант индивидуального задания.
- •Литература
§ 9. Линии 2-го порядка
9.1. Эллипс
1.
Возьмем на плоскости две точки
![]()
Опр.Эллипсом называется множество точек плоскости, для каждой из которых сумма расстояний до двух данных точек, называемых фокусами,
есть величина постоянная, большая расстояния между фокусами.
2. Составим уравнение эллипса.
В ыберем
систему координат
ыберем
систему координат![]()
![]() Пусть точка
Пусть точка
![]()
принадлежит
эллипсу
![]()
![]()



![]() (3)
(3)
Преобразуем уравнение (1), возводя в квадрат обе части:
![]()
![]()
![]()
![]()
 (4)
(4)
Мы
показали, что координаты точек эллипса
удовлетворяют уравнению (4). Но при
переходе от (3) к (4) мы дважды возводили
уравнение в квадрат, при этом могли
появиться лишние корни. Убедимся, что
точки, координаты которых удовлетворяют
уравнению (4), принадлежат эллипсу, то
есть
![]()
 =
=
 Аналогично:
Аналогично:

Так
как
![]() то
то Из (2)
Из (2) поэтому
поэтому
 Значит,
Значит,
 (5)
(5)
![]()
Уравнение (4) называется каноническим уравнением эллипса.
Формулы (3) дают фокальные радиусы эллипса
3.Исследование формы эллипса.
Е сли
сли![]() то
то![]() То есть у эллипса есть две оси симметрии
То есть у эллипса есть две оси симметрии![]() и
и![]() центр симметрии
центр симметрии![]() Точки
пересечения эллипса с осями координат
называются еговершинами.
Пользуясь симметрией эллипса, рассмотрим
его форму в 1 четверти.
Точки
пересечения эллипса с осями координат
называются еговершинами.
Пользуясь симметрией эллипса, рассмотрим
его форму в 1 четверти.

При
росте
![]() от 0 до
от 0 до![]()
![]() убывает от
убывает от![]() до 0.
до 0.
Продолжим чертеж симметрично в другие четверти.
Как
видно, эллипс – линия ограниченная,
расположенная в прямоугольнике
![]() Вершины
Вершины![]() центр
эллипса.
центр
эллипса.
Заметим, что фокусы эллипса всегда принадлежат большей оси.
Пример.

![]()
4. Эксцентриситет эллипса.
Опр.Эксцентриситет
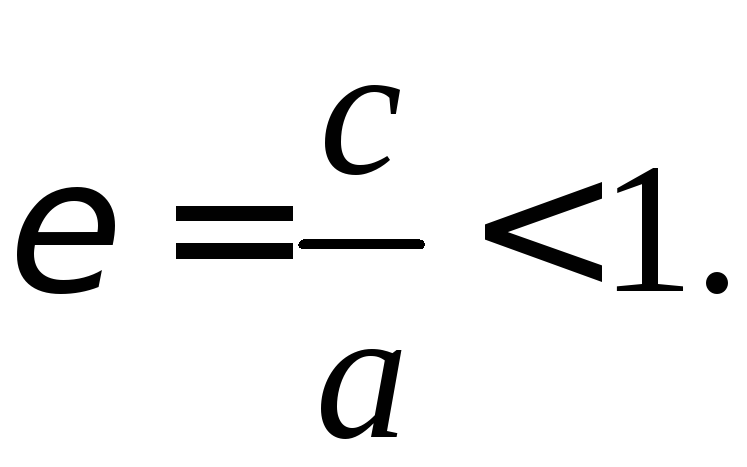
При
![]() фокусы совпадают:
фокусы совпадают:![]() эллипс является окружностью. Найдем:
эллипс является окружностью. Найдем:
Как
видно, чем меньше
![]() тем дробь
тем дробь![]() ближе к 1, то есть эллипс становится
шире. Чем больше
ближе к 1, то есть эллипс становится
шире. Чем больше![]() тем больше эллипс вытянут вдоль оси
тем больше эллипс вытянут вдоль оси![]()
5. Параметрические уравнения эллипса.
П усть
задан эллипс
усть
задан эллипс
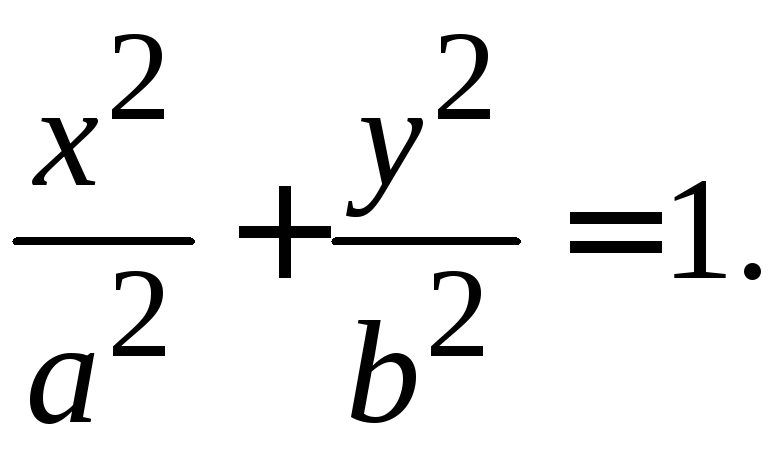 Построим две
Построим две
окружности
![]()
Произвольный
луч под углом
![]() к оси
к оси![]()
пересекает
их в точках
![]() Построим точку
Построим точку![]() Очевидны равенства:
Очевидны равенства:
 (6)
(6)
Подставив
(6)в уравнение эллипса, получим верное
равенство, следовательно, точка
![]() принадлежит эллипсу. Уравнения (6)
называютсяпараметрическими
уравнениями
эллипса.
принадлежит эллипсу. Уравнения (6)
называютсяпараметрическими
уравнениями
эллипса.
Замечание.
Можно доказать обратное утверждение:
если точка принадлежит эллипсу, то
найдется значение параметра
![]() такое, что выполняются соотношения (6).
такое, что выполняются соотношения (6).
Отсюда ясен способ построения эллипса.
6. Директрисы эллипса.
О пр.Директрисами
эллипса
называются прямые, параллельные малой
оси и отстоящие от неё на расстояние
пр.Директрисами
эллипса
называются прямые, параллельные малой
оси и отстоящие от неё на расстояние
![]()
Очевидны уравнения директрис:

Найдем
отношение расстояний точки
![]() эллипса до фокуса и до соответствующей
директрисы. Расстояния до фокусов дают
формулы (5):
эллипса до фокуса и до соответствующей
директрисы. Расстояния до фокусов дают
формулы (5):

Расстояния
до директрис: Отсюда:
Отсюда:
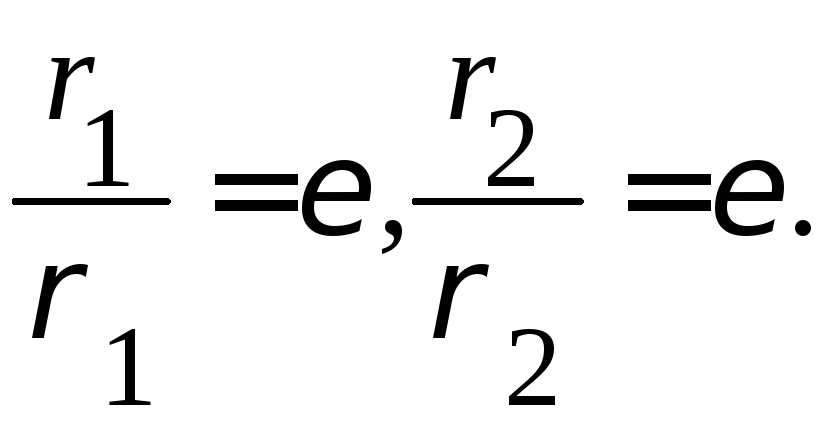
Свойство директрис эллипса: эллипс есть множество точек, отношение расстояний от каждой из которых до фокуса к расстоянию до соответствующей директрисы постоянно и равно эксцентриситету.
Задача.
Составьте уравнение эллипса, если
расстояние между директрисами
![]() а между фокусами
а между фокусами![]()

9.2. Гипербола
1.Опр.
Гиперболой
называется
множество точек плоскости, для которых
абсолютное значение разности расстояний
до двух фиксированных точек
![]() (фокусов) есть величина постоянная,
меньшая расстояния между фокусами.
(фокусов) есть величина постоянная,
меньшая расстояния между фокусами.
2. Составим уравнение гиперболы.
![]()

В
системе координат
 (7)
(7)
Возведя обе части уравнения в квадрат, получим после упрощения:

 (8)
(8)
Это каноническое уравнение гиперболы.
Итак, если точка принадлежит гиперболе, то её координаты удовлетворяют уравнению (8). Можно показать и обратное: если координаты точки удовлетворяют уравнению (8), то точка принадлежит гиперболе.
3. Исследование формы гиперболы.
Из уравнения (8) видно, что гипербола симметрична относительно осей координат. Пользуясь симметрией, исследуем форму гиперболы в 1 четверти системы координат.
Из
(8)

В
полосе
![]() точек гиперболы нет. Далее с ростом
точек гиперболы нет. Далее с ростом![]() величина
величина![]() неограниченно растет. При
неограниченно растет. При![]()
![]() этовершина
гиперболы.
этовершина
гиперболы.
П ользуясь
симметрией, можно достроить
ользуясь
симметрией, можно достроить
гиперболу.
Ось
![]() фокальная
фокальная
(действительная)
ось,
![]() мнимая ось, её
мнимая ось, её
гипербола
не пересекает.![]()
Как
ведет себя ветвь гиперболы при
неограниченном возрастании
![]()
Рассмотрим
прямую
 Убедимся, что уходя в бесконечность,
точка
Убедимся, что уходя в бесконечность,
точка![]() на
гиперболе неограниченно приближается
к этой прямой, то есть
на
гиперболе неограниченно приближается
к этой прямой, то есть![]()
![]() тем более),
тем более),![]()
гипербола.
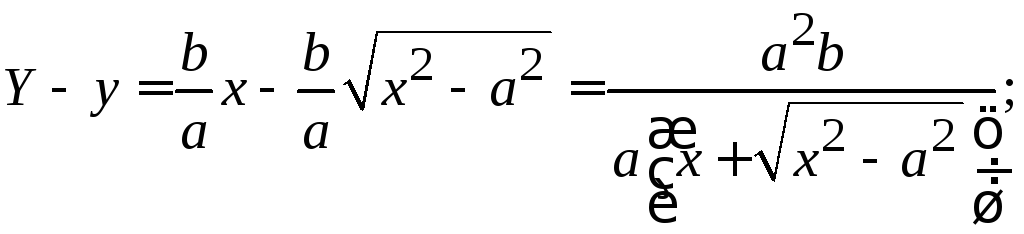
![]() .
.
Если при удалении точки по кривой в бесконечность её расстояние от некоторой прямой стремится к 0, то эта прямая называется
асимптотой кривой.
Учитывая симметрию,
приходим к выводу, что гипербола имеет
две асимптоты:
Построение гиперболы:

![]() действительная
полуось,
действительная
полуось,
![]() мнимая
полуось.
мнимая
полуось.
Эксцентриситет и директрисы гиперболы.
 Директрисы
располагаются ближе к оси
Директрисы
располагаются ближе к оси
![]() чем вершины гиперболы, а фокусы дальше.
чем вершины гиперболы, а фокусы дальше.
Как
и у эллипса, отношение расстояния от
точки гиперболы до фокуса к её расстоянию
до соответствующей директрисы равно
![]()
 Значит, чем меньше
Значит, чем меньше
![]() ,
тем меньше отношение
,
тем меньше отношение![]() тем больше гипербола вытягивается вдоль
действительной оси.
тем больше гипербола вытягивается вдоль
действительной оси.
Равносторонняя и сопряженные гиперболы.
Если
![]() то
то![]() это равносторонняя гипербола.
это равносторонняя гипербола.
Гиперболы
 называютсясопряженными.
Фокусы первой
гиперболы лежат на оси
называютсясопряженными.
Фокусы первой
гиперболы лежат на оси
![]() мнимая ось для неё
мнимая ось для неё![]() Асимптоты этих гипербол совпадают.
Асимптоты этих гипербол совпадают.
Задача.
Составьте
каноническое уравнение гиперболы, угол
между асимптотами которой
![]() ,
и она проходит через точку
,
и она проходит через точку![]()
Сделайте
чертёж.

