§ 2. Деление отрезка в данном отношении

Точкии, заданные на плоскости, определяют направленный отрезок.

Опр. Точка делит направленный отрезокв отношении, если.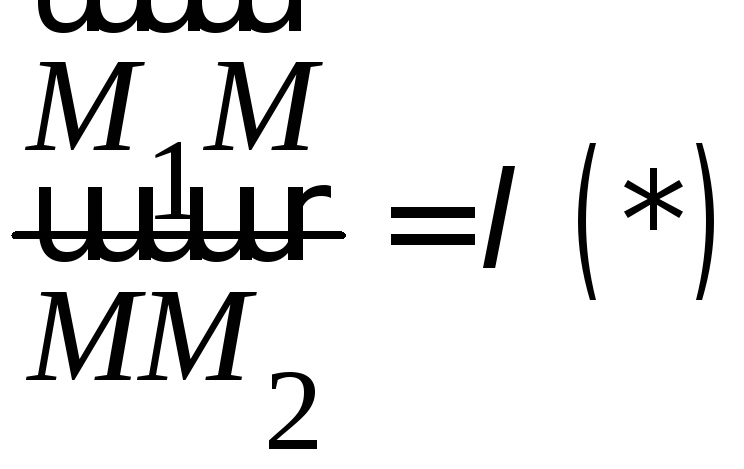

Число называется такжепростым отношением 3-х точек. может быть >0, <0, ноПриточкаделит отрезоквнешним образом.

Поставим задачу: по известным координатам концов отрезка и числу найти координаты делящей точки

Из равенства еслито

По свойству координат имеем: Отсюда:

(6)

Задача. Рассмотрите случай

§3. Декартова прямоугольная система координат

Опр. Система координат называется декартовой прямоугольной, если в качестве базиса взят ортонормированный базис

В таком базисе мы умеем считать длину вектора:

Найдем расстояние между двумя точками и

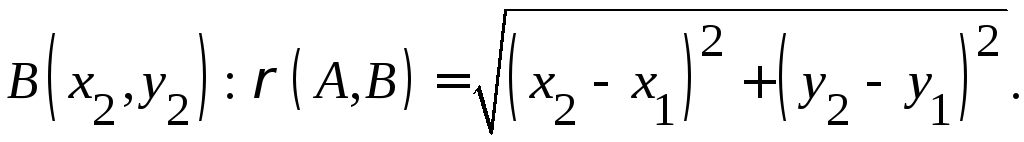
Пример. В Определите длину биссектрисы

§ 4. Ориентация плоскости

На плоскости существует множество базисов. Рассмотрим два из них:

Аи В.Векторы второго базиса разложим по векторам первого:

(7)

Матрица 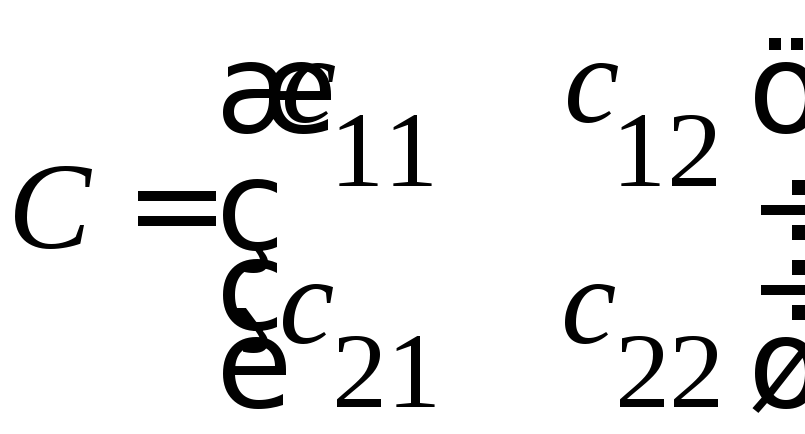называетсяматрицей перехода от базиса А к базису В.

Её определитель

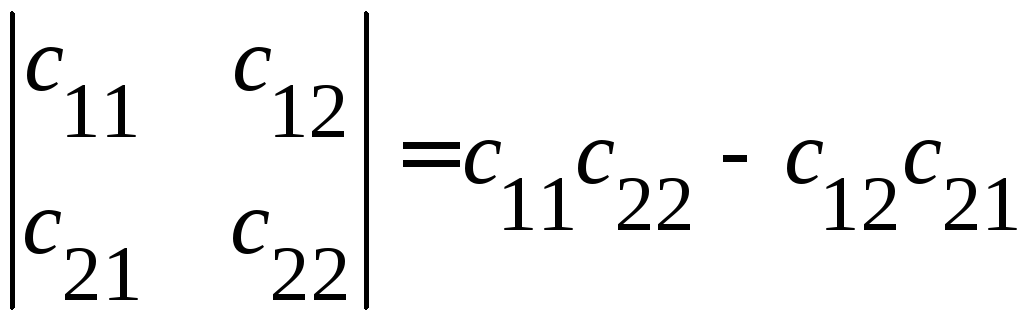(8)

называется определителем матрицы перехода. Он отличен от 0, так как в противном случае его строки были бы пропорциональны, следовательно, векторы не составляли бы базиса.

Матрица с определителем, отличным от 0, называется невырожденной.

Отметим свойства определителя (8).

Два базиса, определитель матрицы перехода которых >0, называются одинаково ориентированными; и противоположно ориентированными, если определитель <0. Все базисы делятся на два класса, базисы одного класс считают правыми и положительно ориентированными, базисы другого – левыми или отрицательно ориентированными.

Опр. Плоскость называется ориентированной, если на ней выбран базис.

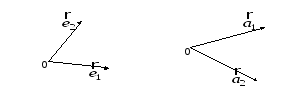
Правый базис Левый базис

Вместе с базисом на плоскости задается аффинный репер или аффинная система координат. Плоскость ориентирована, если на ней выбрана система координат.

Угол на плоскости называется ориентированным, если принимается во внимание порядок, в котором заданы его лучи. Угол называетсяположительно ориентированным, если репер положительно ориентирован. Все правые реперы положительно ориентированы, в них отсчет угла ведется против часовой стрелки.

§5. Полярные координаты

величина направленного угла.

Задача. Назовите координатные линии полярной системы.

Установим связь между полярными и декартовыми прямоугольными координатами точки. Для этого к полярной системе присоединим репер

Пусть и( 9)

Обратно: (10)

или

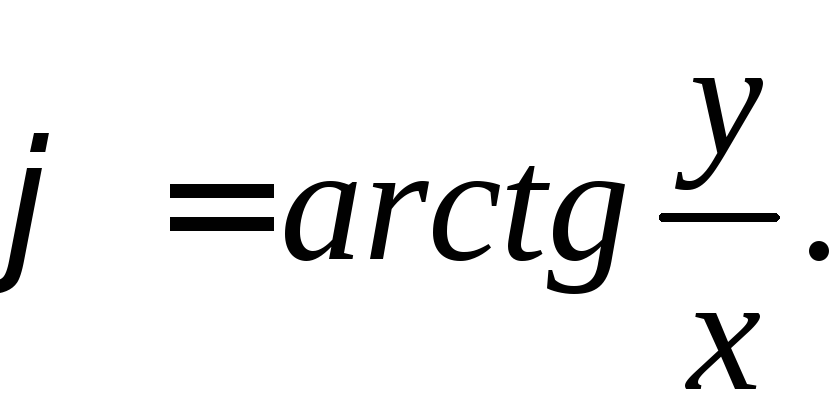
§6. Алгебраическая линия

Введение системы координат на плоскости позволяет использовать

при решении задач метод координат. При использовании этого метода каждая фигура задается с помощью уравнения или неравенства. При этом мы имеем дело с аналитическим методом решения задачи, а геометрия называется аналитической. В ней решаются две задачи:

1) по заданным свойствам фигуры составить аналитические условия, её определяющие;

2)по аналитическим свойствам , задающим фигуру, исследовать её свойства.

Очень часто на плоскости рассматривают геометрическую фигуру, называемую линией. Она задается своим уравнением: уравнение, которому удовлетворяют координаты любой точки этой линии и не удовлетворяют координаты посторонней точки.

Опр. Линия на плоскости называется алгебраической, если в некоторой аффинной системе координат её уравнение можно представить в виде гдемногочлен от переменных

Степень этого многочлена называется порядком линии.

Примеры:

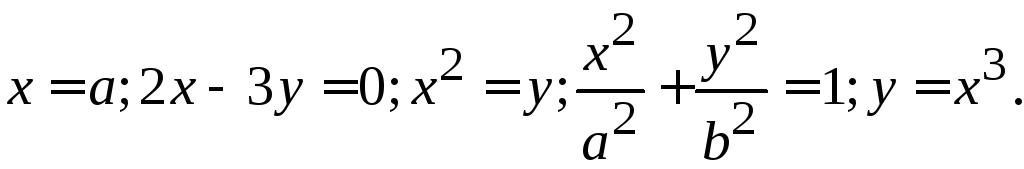
Задача. Записать уравнение окружности с центром в точке и радиусом

Это линия 2-го порядка.

Частный случай:

Примеры неалгебраических линий: и т.д.

Задача. При каких условиях на коэффициенты уравнение

определяет окружность в дпск?

Задача. Определите координаты центра и радиус окружности