
- •Безверхняя и. С.
- •§2. Линейные операции над векторами
- •§3. Линейная зависимость векторов
- •§4. Координаты вектора
- •§5. Скалярное произведение векторов
- •§6. Направляющие косинусы вектора
- •§7. Векторное произведение векторов.
- •§8. Смешанное произведение векторов.
- •Раздел 2. Метод координат на плоскости
- •§1. Аффинная система координат
- •§ 2. Деление отрезка в данном отношении
- •§3. Декартова прямоугольная система координат
- •§ 4. Ориентация плоскости
- •§5. Полярные координаты
- •§6. Алгебраическая линия
- •§7. Прямая линия на плоскости
- •7.1.Различные уравнения прямой
- •7.3. Взаимное расположение двух прямых
- •7.4. Прямая в декартовой прямоугольной системе координат
- •§8. Формулы преобразования координат
- •§ 9. Линии 2-го порядка
- •9.1. Эллипс
- •9.2. Гипербола
- •9.3. Парабола
- •9.4. Кривые 2-го порядка как конические сечения
- •§10. Общее уравнение линии 2-го порядка
- •Часть 1. Преобразуем систему координат поворотом на угол вокруг начала.
- •Часть 2. Исследуем уравнение (17):
- •Раздел 3. Система координат в пространстве
- •§1. Плоскость
- •§2. Взаимное расположение двух плоскостей
- •§3.Плоскость в дпск. Основные задачи.
- •§4. Прямая в пространстве.
- •§5. Поверхности 2-го порядка
- •5.1. Понятие поверхности 2-го порядка
- •5.2. Цилиндрические поверхности.
- •5.3. Конические поверхности
- •5.4. Эллипсоид
- •5.5 Однополостный гиперболоид
- •5.6. Двуполостный гиперболоид
- •5.7. Эллиптический параболоид
- •5.8. Гиперболический параболоид
- •Вариант индивидуального задания.
- •Литература
§5. Скалярное произведение векторов
Опр.
Скалярным произведением двух векторов
называется число, равное произведению
их длин на косинус угла между ними:
![]()
![]()
Свойства скалярного произведения
1.
![]() (очевидно из определения).
(очевидно из определения).
2.
![]() ,
то есть числовой множитель можно выносить
за знак скалярного произведения.
,
то есть числовой множитель можно выносить
за знак скалярного произведения.
∆
![]()
![]()
а)
![]() Правые части равны,
Правые части равны,
![]() значит, равны
и левые.
значит, равны
и левые.
б)
![]() ,
,
![]()
И в этом случае правые части равны, значит, равны и левые. Свойство доказано.
3.
![]() (признак перпендикулярности векторов).
(признак перпендикулярности векторов).
4. Скалярный квадрат вектора равен квадрату его модуля:
![]()
5.
Скалярное произведение векторов
![]() и
и![]() ,
заданных в ортонормированном базисе
,
заданных в ортонормированном базисе![]() ,
выражается формулой:
,
выражается формулой:![]()
∆ Пусть
![]() не нулевые и не коллинеарные векторы.
Отложим их от одной точки пространства.
не нулевые и не коллинеарные векторы.
Отложим их от одной точки пространства.
 Применим
к
Применим
к
![]() теорему косинусов:
теорему косинусов:
![]() ,
,
![]()
![]()

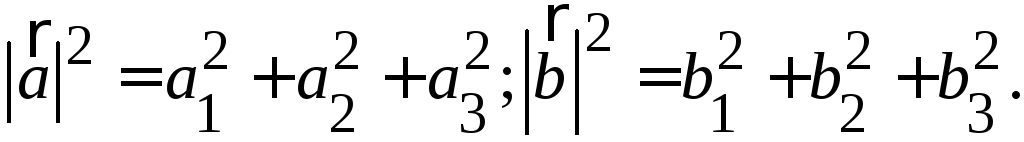 Подставляя в
равенство
Подставляя в
равенство
![]() получим:
получим:
![]()
![]()
![]() ▲
▲
Задача.
Рассмотрите случай
![]()
6.
![]() При доказательстве используется свойство
5.
При доказательстве используется свойство
5.
7.

§6. Направляющие косинусы вектора
![]() .
Умножим скалярно на вектор
.
Умножим скалярно на вектор
![]() .
.
![]()
Аналогично
получим:
![]()
Обозначим
углы:
![]()
![]() (4)
(4)
Числа
![]() называютсянаправляющими
косинусами вектора
называютсянаправляющими
косинусами вектора
![]()
Из равенств (4) следует, что каждая координата вектора равна произведению его модуля на соответствующий направляющий косинус (в ортонормированном базисе).
Из
(4):
![]() то есть
то есть
![]() (5)
(5)
§7. Векторное произведение векторов.
7.1. Правые и левые тройки векторов.
Три произвольных
вектора
![]() ,
рассматриваемые в определенном порядке,
называютсяупорядоченной
тройкой.
Упорядоченная тройка некомпланарных
векторов
,
рассматриваемые в определенном порядке,
называютсяупорядоченной
тройкой.
Упорядоченная тройка некомпланарных
векторов
![]() считаетсяправой,
если эти векторы расположены так же,
как большой, указательный и средний
пальцы правой руки. Если они располагаются,
как те же пальцы левой руки, то тройка
называется левой.
считаетсяправой,
если эти векторы расположены так же,
как большой, указательный и средний
пальцы правой руки. Если они располагаются,
как те же пальцы левой руки, то тройка
называется левой.
7.2. Определение и свойства векторного произведения.
Опр.
Векторным
произведением
вектора
![]() на вектор
на вектор![]() называется
такой третий вектор
называется
такой третий вектор![]() ,
который
,
который
и
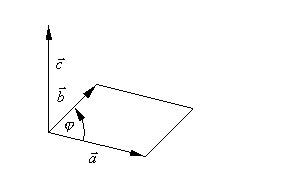
 меет
модуль, численно равный площади
параллелограмма, построенного на
векторах
меет
модуль, численно равный площади
параллелограмма, построенного на
векторах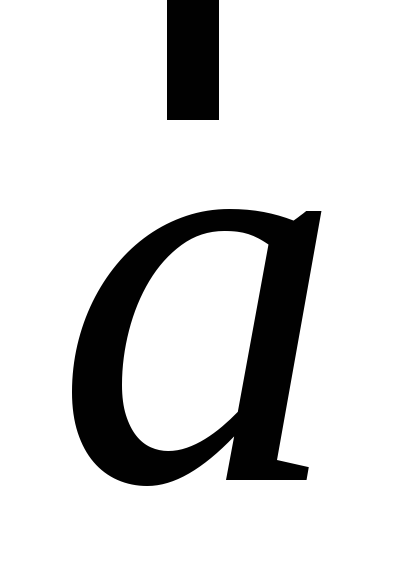 и
и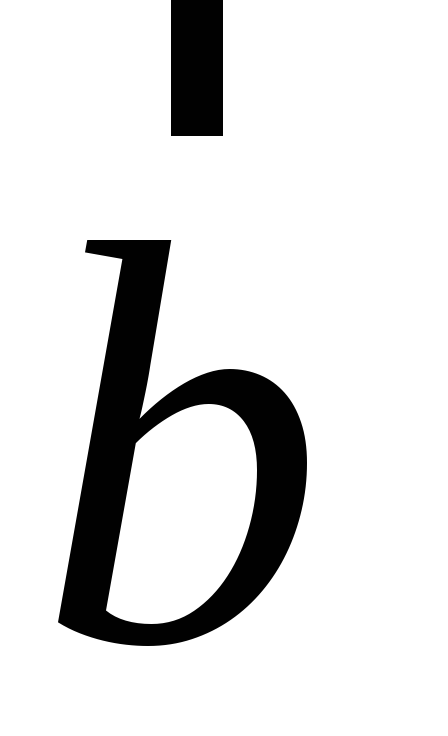 :
: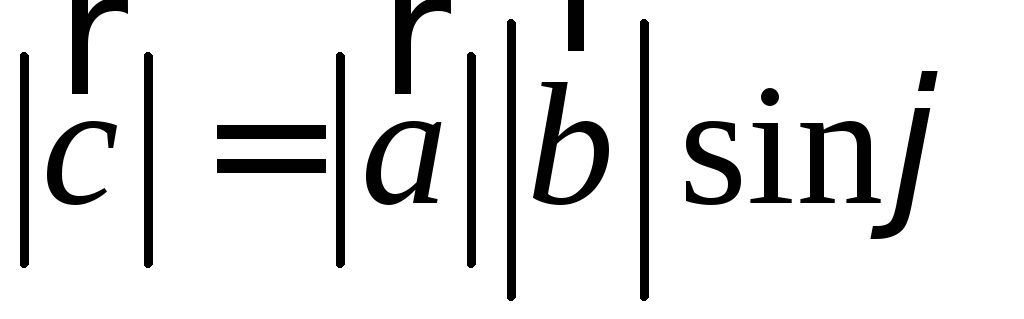 ;
;ортогонален каждому из векторов
 и
и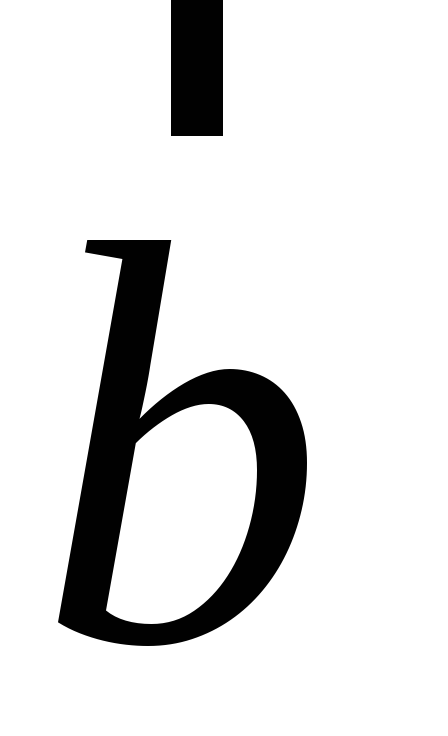 ;
;направлен так, что тройка векторов
 - правая.
- правая.
Обозначение
векторного произведения:
![]() или
или![]() .
.
Свойства векторного произведения.
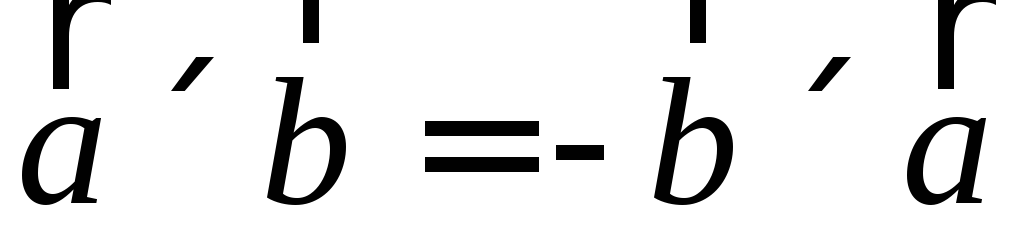 (антикоммутативность),
(антикоммутативность),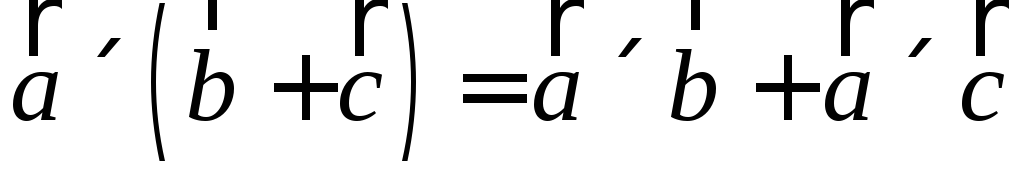 (распределительный
закон),
(распределительный
закон),Если
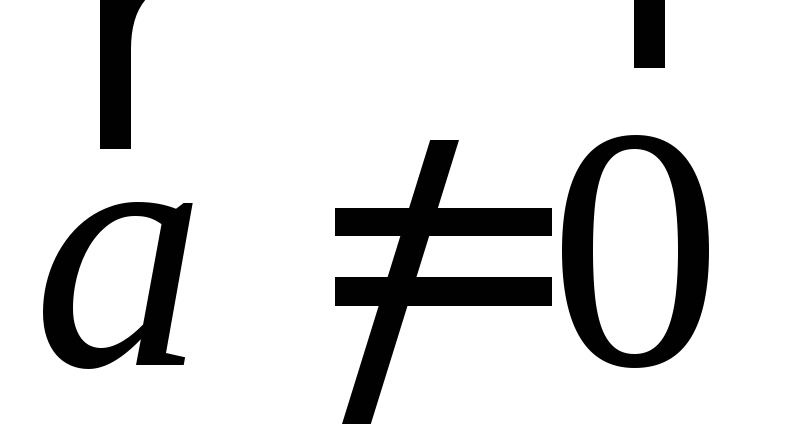 и
и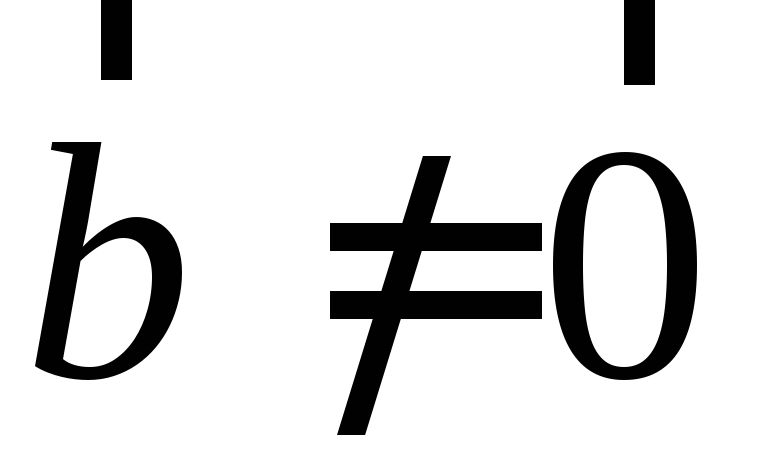 ,
то
,
то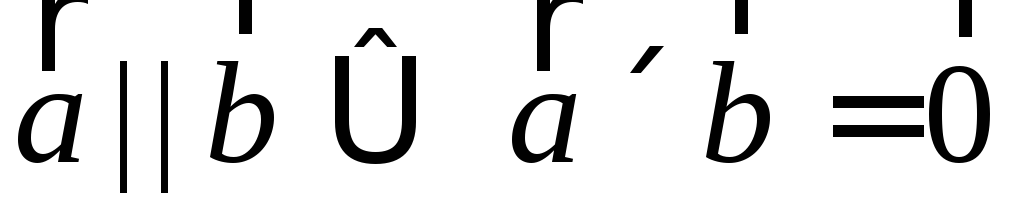 ,
в частности
,
в частности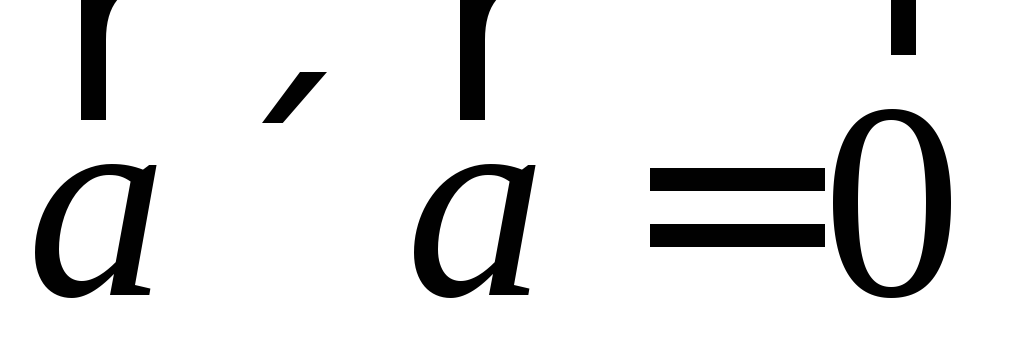 ,
,Векторное произведение ортов:
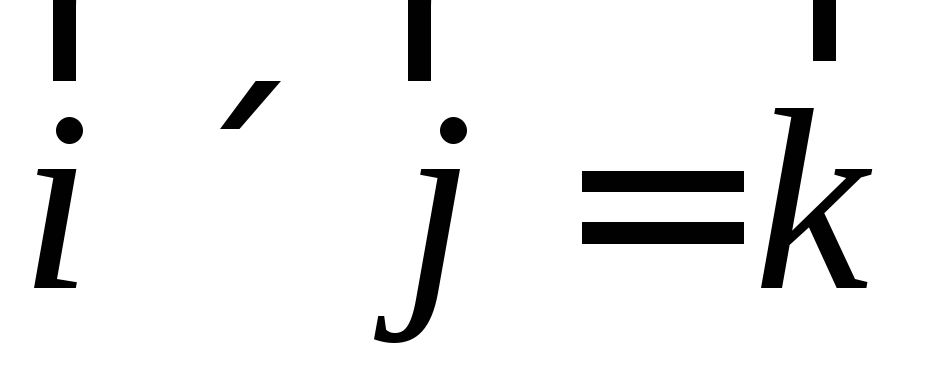 ,
,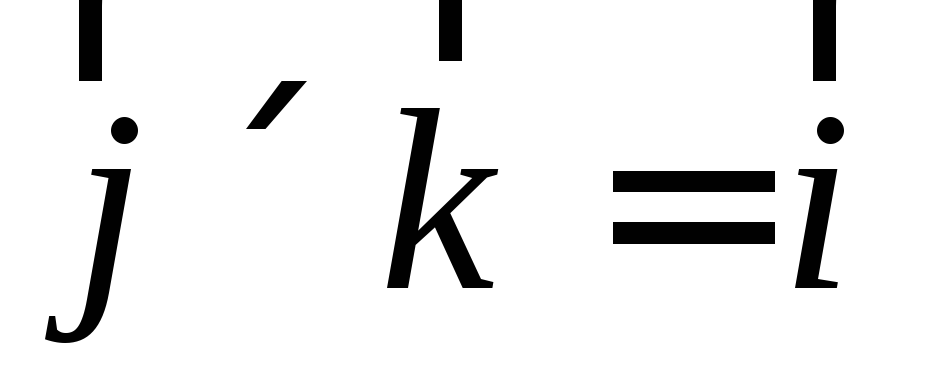 ,
,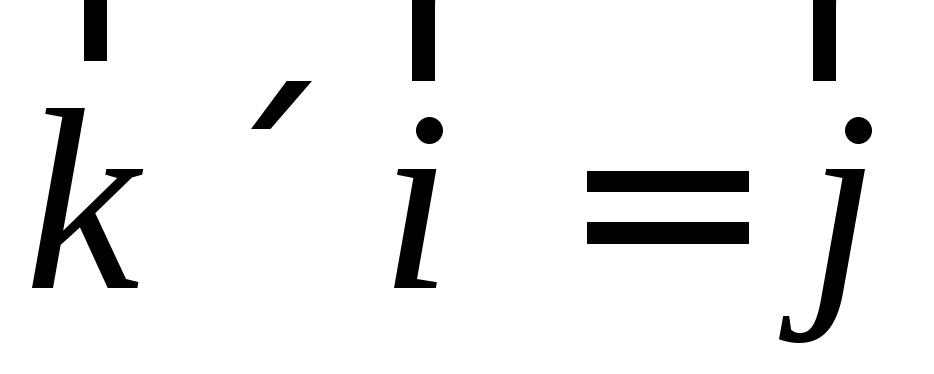 .
.
Вообще
произведение любых смежных векторов в
последовательности
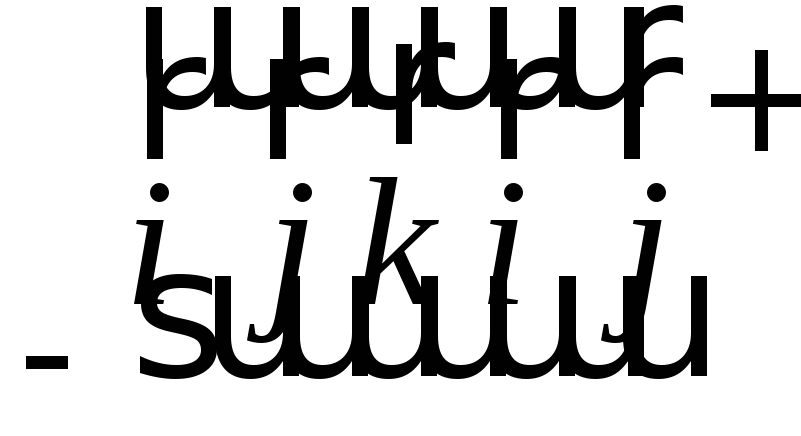 дает следующий вектор со знаком «+», а
в обратной последовательности – со
знаком «-».
дает следующий вектор со знаком «+», а
в обратной последовательности – со
знаком «-».
Для любого вещественного числа
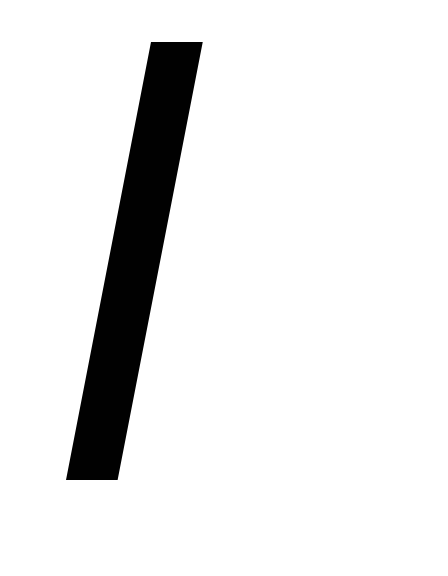 справедливы соотношения:
справедливы соотношения:
![]()
Выражение векторного произведения через координаты сомножителей
 ,
,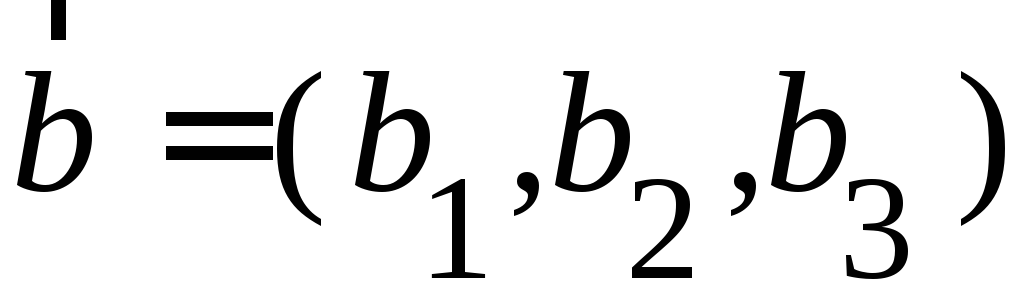 в декартовой прямоугольной системе
координат.
в декартовой прямоугольной системе
координат.
![]()
![]() =
=![]()
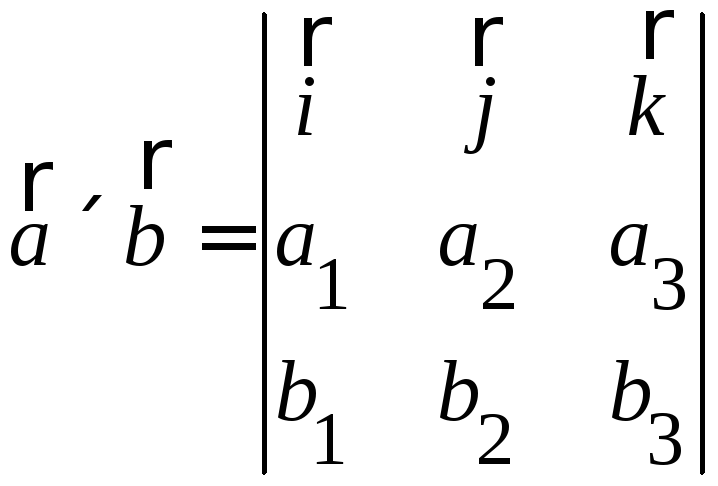
Геометрический смысл модуля векторного произведения: площадь параллелограмма, построенного на векторах
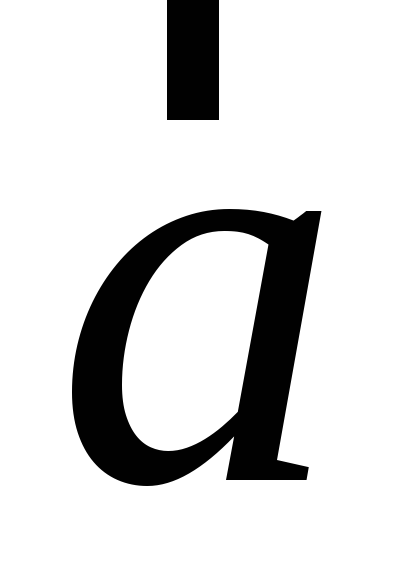 и
и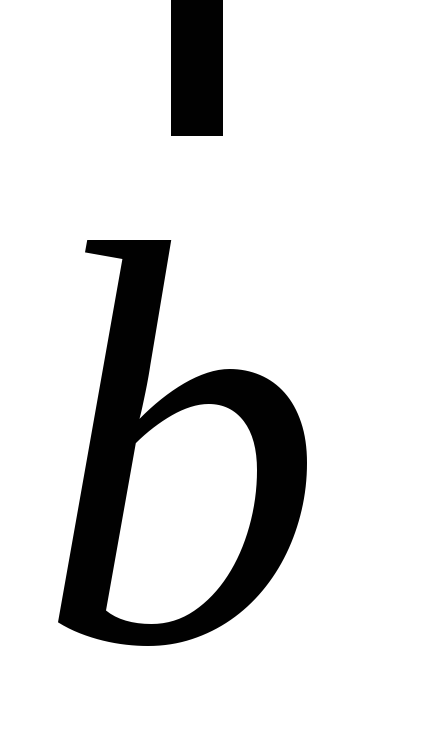 :
: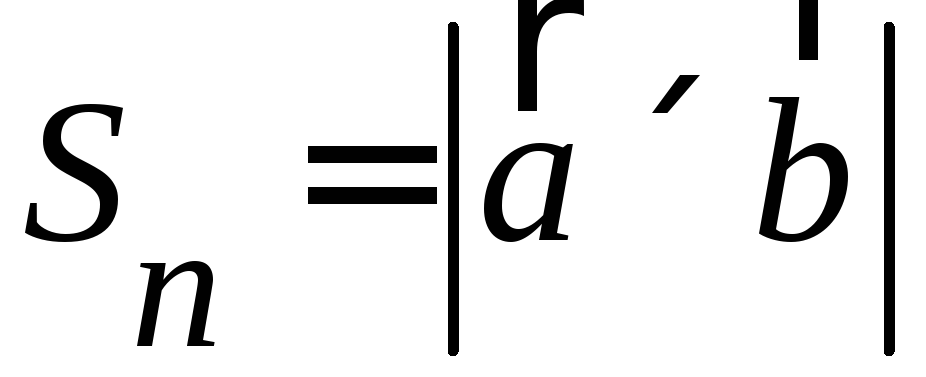 ;
;
Площадь
треугольника, построенного на векторах
![]() и
и![]() ,
равна
,
равна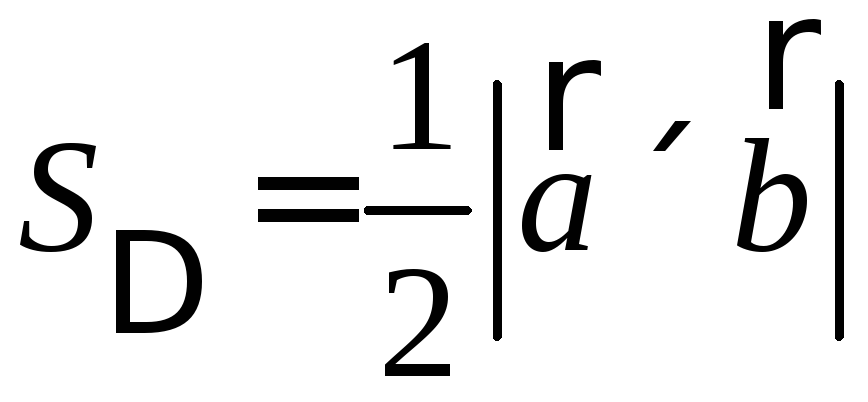 .
.
Пример
1. Вычислите
площадь параллелограмма, построенного
на векторах
![]() ,
,![]() ,
если
,
если![]() ,
,![]() ,
, .
.
Решение.
![]() .
.
1)
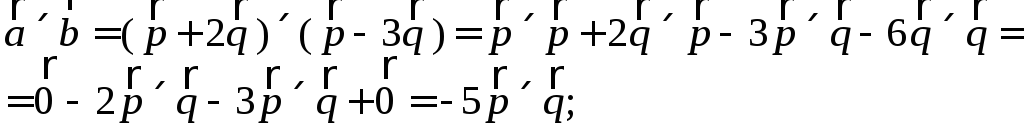
2)
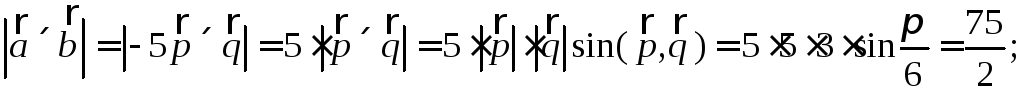
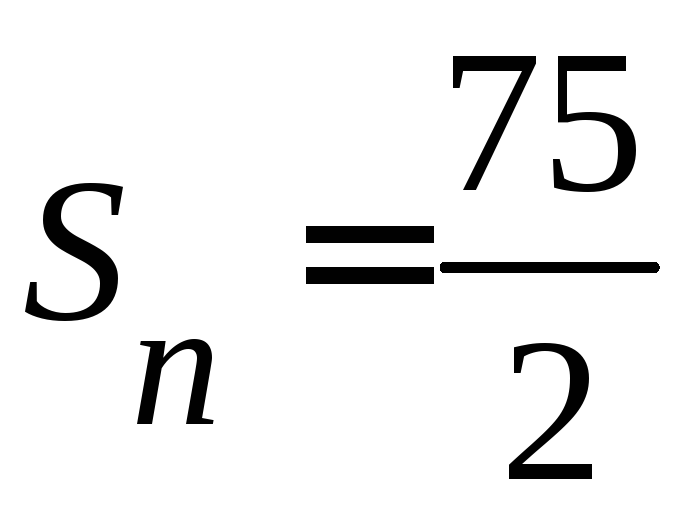 .
.
Пример
2. Найдите
площадь треугольника, построенного на
векторах
![]() ,
,![]()
Решение.
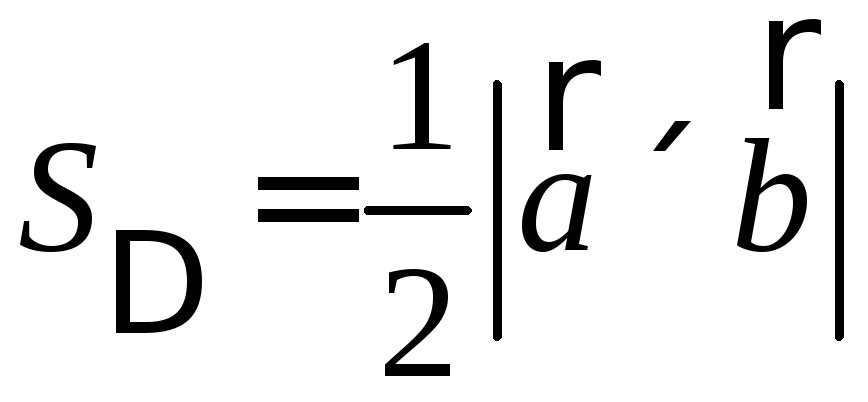
Найдем вектор
 .
.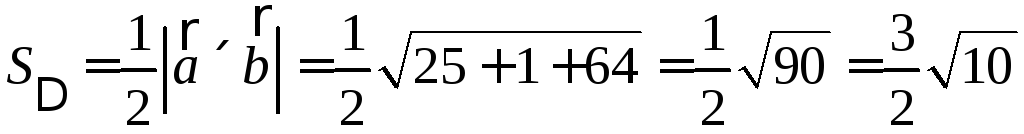 .
.
