Федеральное агентство по образованию РФ

ГОУВПО Тульский государственный педагогический университет

им. Л. Н. Толстого

Кафедра алгебры и геометрии

Безверхняя и. С.

Конспект лекций по курсу «Геометрия»

Часть 1. Аналитическая геометрия

для студентов факультета математики, физики и информатики

Тула - 2006

Раздел 1. Элементы векторной алгебры

§1. Основные определения

Опр. Отрезок называется направленным, если принимается во внимание порядок его концов:начало,конец.

Опр. Направленный отрезок называется вектором:

Если имеем нуль – вектор или нулевой вектор

Опр. Отрезки иодинаково направлены (сонаправлены), если одинаково направлены лучи и

Опр. Векторы иназываютсяпротивоположными.

Опр. Векторы, параллельные одной прямой, называются коллинеарными.

Опр. Длина соответствующего направленного отрезка называется модулем или длиной вектора.

Опр. Векторы равны, если равны их длины и одинаковы направления.

Мы будем рассматривать свободные векторы, то есть те, которые можно откладывать от любой точки.

Как видно, в отличие от скалярной величины которая характеризуется только числом (площадь, объем, температура и т.д.), вектор более сложное понятие, для него нужно указать и длину, и направление (скорость, ускорение, момент силы и т.д.).

§2. Линейные операции над векторами

К линейным относятся операции сложения и вычитания векторов и умножения вектора на число.

2.1. Сложение векторов

Правило треугольника

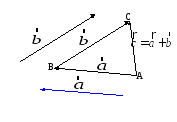Сумма векторов:

Как видно, здесь строится .

Для любых трех точек А, В и С справедливо равенство:

Правило параллелограмма Правило многоугольника

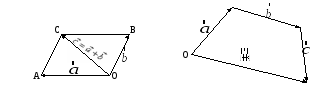
Теорема 1. Сложение векторов обладает свойствами:

1.

2.

3. (коммутативность сложения);

4. (ассоциативность сложения).

∆ 1.Пусть

2.Пусть

3.Смотри правило параллелограмма.

4. Смотри правило многоугольника:

▲

2.2..Вычитание векторов

Опр. Разностью двух векторов иназывается вектортакой, что

Найдем вектор Для этого прибавим к обеим частям последнего равенства вектор:

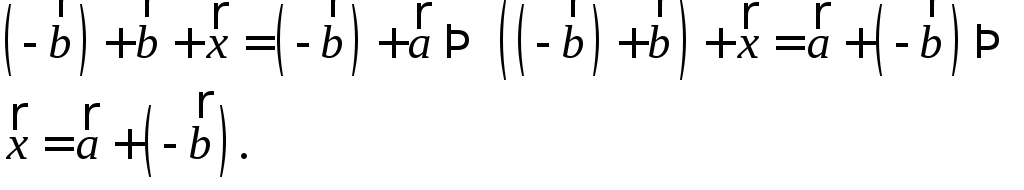
Итак, разность векторов всегда существует. Её обозначают так:

2.3. Умножение вектора на число

Пусть некоторый вектор,вещественное число.

Опр. Произведением вектора на числоназывается такой вектор, который удовлетворяет условиям:

1)

2) , если,

, если .

Условиями 1) и 2) вектор определяется однозначно.

или , то естьи.

Теорема 2. Умножение вектора на число обладает свойствами:

1.

2.

3.

4. .

∆ Докажем первые два свойства.

1. Обозначим и покажем, что.

, то есть .

2. Обозначим .

Векторы иимеют одну и ту же длину.

Возможны случаи:

и и

и

И т.д.

Направления векторов ивсегда совпадают, длины их равны. Следовательно,▲

2.4. Векторные пространства

Рассмотрим все множество векторов и определим в нем линейные операции сложения и умножения на число. Такое множество называетсялинейным пространством, если при этом выполняются условия 1-4 для сложения и 1-4 для умножения на число.

Примеры векторных пространств:

Множество вещественных квадратных матриц 2-го порядка является 4-мерным линейным пространством.